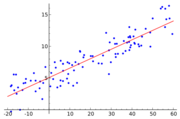
انكفاء خطي
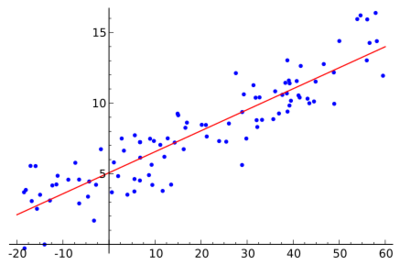
في الاحصاء، يقال إن الانكفاء خطي linear regression إذا أمكن تسوية الخط المضلعي للانكفاء بمستقيم، وتكتب معادلة هذا المستقيم، في هذه الحالة، بالصيغة: ع=أ+ب س،، كما يمكن أن تكتب بالصيغة: 0ع(س)=ع+ب(س-س)، حيث تعطى ب ، وتسمى معامل الانكفاء، بالعلاقة:
![]() ويعطي هذا المعامل وسطياً، فكرةً عن تأثير تغيرات س على ع انطلاقاً من مجموعة المشاهدات. كذلك على نحو مماثل يمكن كتابة معادلة مستقيم الانكفاء لـ س بدلالة ع. إن هذين المستقيمين اللذين يمران من النقطة المتوسطة ن(س،ع) هما بوجه عام مختلفان، ولا يتطابقان إلا في الحال التي تقع فيها النقط نى على استقامة واحدة (وهي حال الارتباط الخطي التام بين المتغيريْن).[1]
ويعطي هذا المعامل وسطياً، فكرةً عن تأثير تغيرات س على ع انطلاقاً من مجموعة المشاهدات. كذلك على نحو مماثل يمكن كتابة معادلة مستقيم الانكفاء لـ س بدلالة ع. إن هذين المستقيمين اللذين يمران من النقطة المتوسطة ن(س،ع) هما بوجه عام مختلفان، ولا يتطابقان إلا في الحال التي تقع فيها النقط نى على استقامة واحدة (وهي حال الارتباط الخطي التام بين المتغيريْن).[1]
ولتعيين مستقيمات الانكفاء تُستخدم طريقة «المربعات الأصغرية»، فمستقيم الانكفاء هو ذاك المستقيم الذي يجعل مجموع المربعات أصغرياً
، وذلك بفرض أن نى نَى قطعة مستقيمة موازية لأحد المحورين الإحداثيين وأن نَى تقع على مستقيم الانكفاء. فإذا كان المطلوب مستقيم الانكفاء لـ ع بدلالة س كان:
يسمى مربع معامل الانكفاء الخطي س بدلالة ع «مُعامل التحديد» وهو يعطى بالعلاقة:
![]()
ويمثل المقدار
التباين الكلي، و
التباين المفسَّر explained variation، ويحسب هذا من معادلة الانكفاء الخطي.
أما إذا فُرض أن المتغير ع تابع لعدة متغيرات س1،س2،... ، فان فرضية الانكفاء الخطي المتعدد تقود إلى البحث، بطريقة المربعات الأصغرية، عن معادلة انكفاء من الصيغة: ع(س1،س2،... )=أ+ب1س1+ب2س2+... حيث تبين معاملات الانكفاء الجزئية ب1،ب2،... أثر تغيّر كل من المتغيرات س1،س2،... في المتغير ع على التوالي. وتعرِّف المعادلة الأخيرة مستوى انكفـاءٍ في فضـاء ذي (ن + 1) بعداً. ويُعيّن مستوى الانكفاء ع بدلالة س1،س2،... بحيث يكون مجموع مربعات المسافات الموازية إلى م ع بين نقط المشاهدة والمستوي أصغرياً. ويقيس مُعاملُ الارتباط ر أو معامل التحديد ر2:
![]()
قوة العلاقة بين القيم الملاحظة للمتغير ع والقيم المقابلة المقدرة من معادلة مستوي الانكفاء.
مقدمة
افتراضات
التفسير
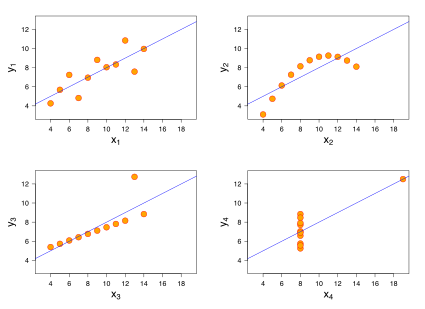
الأنواع
الانكفاء المتعدد والبسيط
النماذج العامة للانكفاء الخطي
Heteroskedastic models
Generalized linear models
Some common examples of GLM's are:
- Poisson regression for count data.
- Logistic regression and probit regression for binary data.
- Multinomial logistic regression and multinomial probit regression for categorical data.
- Ordered probit regression for ordinal data.
النماذج الخطية الهرمية
أخطاء المتغيرات
أخرى
طرق التقدير
تقنيات تقدير أخرى
نقاش مستفيض
خط الاتجاه
علم الأوبئة
المالية
الاقتصاد
العلوم البيئية
انظر أيضاً
- Analysis of variance
- Anscombe's quartet
- Cross-sectional regression
- Curve fitting
- Empirical Bayes methods
- انكفاء لوجستي
- M-estimator
- انكفاء غير خطي
- Nonparametric regression
- Multivariate adaptive regression splines
- Lack-of-fit sum of squares
- Truncated regression model
- Censored regression model
- انكفاء خطي بسيط
- Segmented linear regression
قراءات إضافية
- Pedhazur, Elazar J (1982). Multiple regression in behavioral research: Explanation and prediction (2nd ed.). New York: Holt, Rinehart and Winston. ISBN 0-03-041760-0
- Barlow, Jesse L. (1993). "Chapter 9: Numerical aspects of Solving Linear Least Squares Problems". In Rao, C.R. (ed.). Computational Statistics. Handbook of Statistics. Vol. 9. North-Holland. ISBN 0-444-88096-8
{{cite book}}: CS1 maint: postscript (link) - Björck, Åke (1996). Numerical methods for least squares problems. Philadelphia: SIAM. ISBN 0-89871-360-9.
{{cite book}}: Cite has empty unknown parameter:|coauthors=(help) - Goodall, Colin R. (1993). "Chapter 13: Computation using the QR decomposition". In Rao, C.R. (ed.). Computational Statistics. Handbook of Statistics. Vol. 9. North-Holland. ISBN 0-444-88096-8
{{cite book}}: CS1 maint: postscript (link) - National Physical Laboratory (1961). "Chapter 1: Linear Equations and Matrices: Direct Methods". Modern Computing Methods. Notes on Applied Science. Vol. 16 (2nd ed.). Her Majesty's Stationery Office
{{cite book}}: CS1 maint: postscript (link) - National Physical Laboratory (1961). "Chapter 2: Linear Equations and Matrices: Direct Methods on Automatic Computers". Modern Computing Methods. Notes on Applied Science. Vol. 16 (2nd ed.). Her Majesty's Stationery Office
{{cite book}}: CS1 maint: postscript (link)
هوامش
- ^ محمد شفيق ياسين. "الانكفاء". الموسوعة العربية. Retrieved 2012-06-18.
المصادر
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. (2nd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates
- Charles Darwin. The Variation of Animals and Plants under Domestication. (1868) (Chapter XIII describes what was known about reversion in Galton's time. Darwin uses the term "reversion".)
- Draper, N.R. and Smith, H. Applied Regression Analysis Wiley Series in Probability and Statistics (1998)
- Francis Galton. "Regression Towards Mediocrity in Hereditary Stature," Journal of the Anthropological Institute, 15:246-263 (1886). (Facsimile at: [1])
- Robert S. Pindyck and Daniel L. Rubinfeld (1998, 4h ed.). Econometric Models and Economic Forecasts,, ch. 1 (Intro, incl. appendices on Σ operators & derivation of parameter est.) & Appendix 4.3 (mult. regression in matrix form).
- Kaw, Autar; Kalu, Egwu (2008). "Numerical Methods with Applications" (1st ed.). [2].
{{cite web}}: External link in|publisher=|url=(help), Chapter 6 deals with linear and non-linear regression.
وصلات خارجية