المربعات الأقل
طريقة المربعات الأقل إنگليزية: Least squares هي طريقة تقريب قياسية تستخدم لحل أنظمة المعادلات التي يكون فيها عدد المعادلات أكبر من عدد المتحولات. "المربعات الأقل" تعني بأن الحل الكلي يتجه نحو تصغير قيمة مجموع مربعات الخطأ الناتج عن حل كل معادلة.
من أهم التطبيقات هو الإسقاط الشكلي للبيانات (data fitting). حيث أن أفضل إسقاط شكلي لمجموعة بيانات يتجه نحو تصغير مجموع مربعات الأخطاء، حيث أن الخطأ هو الفرق بين القيمة المقاسة للبيانات والقيمة المسقطة على الشكل. تم وصف مسألة المربعات الأقل للمرة الأولى من قبل كارل گاوس حوالي عام 1794.
منطوق المشكلة
The objective consists of adjusting the parameters of a model function to best fit a data set. A simple data set consists of n points (data pairs) , i = 1, ..., n, where is an independent variable and is a dependent variable whose value is found by observation. The model function has the form , where the m adjustable parameters are held in the vector . The goal is to find the parameter values for the model which "best" fits the data. The least squares method finds its optimum when the sum, S, of squared residuals
is a minimum. A residual is defined as the difference between the actual value of the dependent variable and the value predicted by the model.
- .
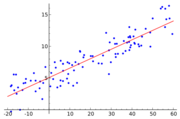
An example of a model is that of the straight line. Denoting the intercept as and the slope as , the model function is given by . See linear least squares for a fully worked out example of this model.
A data point may consist of more than one independent variable. For an example, when fitting a plane to a set of height measurements, the plane is a function of two independent variables, x and z, say. In the most general case there may be one or more independent variables and one or more dependent variables at each data point.
الطريقة
يعود الفضل لكارل فريدريش گاوس في تطوير أساسيات تحليل المربعات الأقل في 1795 حين كان عمره 18 عاماً.[1] وكان لجندر أول من نشر الطريقة.
طالع أيضاً
- Best linear unbiased estimator (BLUE)
- Best linear unbiased prediction (BLUP)
- مبرهنة گاوس-ماركوڤ
- L2 norm
- Least absolute deviation
- Measurement uncertainty
- Quadratic loss function
- Root mean square
- Squared deviations
الهامش
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةbrertscher
المراجع
- Å. Björck (1996). Numerical Methods for Least Squares Problems. SIAM. ISBN 978-0-89871-360-2.
- C.R. Rao, H. Toutenburg, A. Fieger, C. Heumann, T. Nittner and S. Scheid (1999). Linear Models: Least Squares and Alternatives. Springer Series in Statistics.
{{cite book}}: CS1 maint: multiple names: authors list (link) - T. Kariya and H. Kurata (2004). Generalized Least Squares. Wiley.
- J. Wolberg (2005). Data Analysis Using the Method of Least Squares: Extracting the Most Information from Experiments. Springer. ISBN 3-540-25674-1.
- T. Strutz (2010). Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner. ISBN 978-3-8348-1022-9.