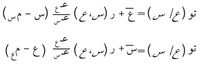انكفاء غير خطي

تحليل الانكفاء
نماذج
انكفاء خطي انكفاء بسيط Ordinary least squares Polynomial regression General linear model Generalized linear model Discrete choice · Logistic regression Multinomial logit · Mixed logit Probit · Multinomial probit Ordered logit · Ordered probit Poisson Multilevel model Fixed effects · Random effects Mixed model Nonlinear regression Nonparametric · Semiparametric Robust · Quantile · Isotonic Principal components · Least angle Local · Segmented Errors-in-variables
التقدير
المربعات الأقل · Ordinary least squares Linear (math) · Partial · Total Generalized · Weighted Non-linear · Iteratively reweighted Ridge regression · LASSO Least absolute deviations Bayesian · Bayesian multivariate
خلفية
Regression model validation Mean and predicted response Errors and residuals Goodness of fit · Studentized residual Gauss–Markov theorem
v t e

See Michaelis-Menten kinetics for details

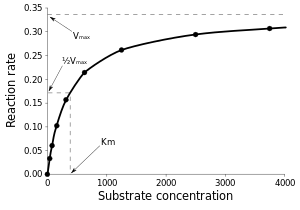
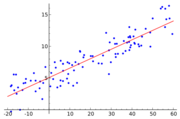
في الاحصاء الانكفاء غير الخطي nonlinear regression هو صيغة لتحليل الانكفاء يمكن فيها التعبير عن القيم الملاحظة لـ ع بدلالة واحد أو أكثر من المتغيرات، بدالّة (تابع) غير خطية لهذه المتغيرات.

من المسائل المطروحة في الإحصاء النظري حالة متغيرين س ، ع عُلِمتْ دالة الكثافة الاحتمالية المشتركة لهما. إن منحني الانكفاء ع بدلالة س في هذه الحال هو مجموعة النقط ذات الإحداثيات [س،تو(ع/س)] حيث يكون تو(ع/س) التوقع الرياضي (أو القيمة الوسطى) لـ ع في التوزيع الشرطي لـ ع من أجل قيمة ما لـ س ( س= س) ويعرَّف كذلك منحني الانكفاء لـ س بدلالة ع. ويعرَّفُ، في حال دالة كثافة لـ ن (عدد المتغيرات) متغيراً وبطريقة مماثلة، سطحُ انكفاء ذو ن + 1 بعداً.

وتبرز أهمية الانكفاء الخطي في حال التوزيع الطبيعي لمتغيرين (وهي حالة شائعة الحدوث)، ويمثَّل مستقيما الانكفاء عندئذ بالمعادلتين:

حيث تتوالى الوسطاء مس، مع، عـس، عـع كما يلي: المتوسطان الحسابيان، والانحرافان المعياريان للتوزيعيين الهامشيين لـ س وع . وأما ر(س،ع) فهو معامل الارتباط لهذين المتغيرين. ويقال الشيء نفسه في حال توزيع طبيعي في ن متغيراً إذ تكون سطوح الانكفاء في هذه الحال مستويات.^[1]

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

عام

احصاء الانكفاء

المربعات الأقل التقليدية والمرجحة

الخطية

التحول

التقسيم

Yield of mustard and soil salinity

المقال الرئيسي: انكفاء قطعي

لوغاريتمات الانكفاء غير الخطي

Gauss–Newton algorithm
gradient descent
Levenberg–Marquardt algorithm: a hybrid of Gauss-Newton and gradient descent

انظر أيضاً

المصادر

^ محمد شفيق ياسين. "الانكفاء". الموسوعة العربية. Retrieved 2012-06-18.

قراءات إضافية

G.A.F Seber and C.J. Wild. Nonlinear Regression. New York: John Wiley and Sons, 1989.
Meade, N. and T. Islam (1995) "Prediction Intervals for Growth Curve Forecasts" Journal of Forecasting, 14:413–430.
K. Schittkowski. Data Fitting in Dynamical Systems. Kluwer, 2002.
R.M. Bethea, B.S. Duran and T.L. Boullion. Statistical Methods for Engineers and Scientists. New York: Marcel Dekker, Inc 1985 ISBN 0-8247-7227-X

الإحصاء

Descriptive statistics

Continuous data

Center	Mean arithmetic geometric harmonic Median Mode
Dispersion	Variance Standard deviation Coefficient of variation Percentile Range Interquartile range
Shape	Central limit theorem Moments Skewness Kurtosis L-moments

Count data

Index of dispersion

Summary tables

Dependence

Graphics

Data collection

Study design	Population Statistic Effect size Statistical power Optimal design Sample size determination Replication Missing data
Survey methodology	Sampling stratified cluster Standard error Opinion poll Questionnaire
Controlled experiments	Scientific control Randomized experiment Randomized controlled trial Random assignment Blocking Interaction Factorial experiment
Adaptive Designs	Adaptive clinical trial Up-and-Down Designs Stochastic approximation
Observational Studies	Cross-sectional study Cohort study Natural experiment Quasi-experiment

Statistical inference

Statistical theory

Frequentist inference

Point estimation	Estimating equations Maximum likelihood Method of moments M-estimator Minimum distance Unbiased estimators Mean-unbiased minimum-variance Rao–Blackwellization Lehmann–Scheffé theorem Median unbiased Plug-in
Interval estimation	Confidence interval Pivot Likelihood interval Prediction interval Tolerance interval Resampling Bootstrap Jackknife
Testing hypotheses	1- & 2-tails Power Uniformly most powerful test Permutation test Randomization test Multiple comparisons
Parametric tests	Likelihood-ratio Score/Lagrange multiplier Wald

Specific tests

Z-test (normal) Student's t-test F-test
Goodness of fit	Chi-squared G-test Kolmogorov–Smirnov Anderson–Darling Lilliefors Jarque–Bera Normality (Shapiro–Wilk) Likelihood-ratio test Model selection Cross validation AIC BIC
Rank statistics	Sign Sample median Signed rank (Wilcoxon) Hodges–Lehmann estimator Rank sum (Mann–Whitney) Nonparametric anova 1-way (Kruskal–Wallis) 2-way (Friedman) Ordered alternative (Jonckheere–Terpstra)

Bayesian inference

Correlation	Pearson product-moment Partial correlation Confounding variable Coefficient of determination
Regression analysis	Errors and residuals Regression validation Mixed effects models Simultaneous equations models Multivariate adaptive regression splines (MARS)
Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression
Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust Heteroscedasticity Homoscedasticity
Generalized linear model	Exponential families Logistic (Bernoulli) / Binomial / Poisson regressions
Partition of variance	Analysis of variance (ANOVA, anova) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical / Multivariate / Time-series / Survival analysis

Categorical

Multivariate

Time-series

General	Decomposition Trend Stationarity Seasonal adjustment Exponential smoothing Cointegration Structural break Granger causality
Specific tests	Dickey–Fuller Johansen Q-statistic (Ljung–Box) Durbin–Watson Breusch–Godfrey
Time domain	Autocorrelation (ACF) partial (PACF) Cross-correlation (XCF) ARMA model ARIMA model (Box–Jenkins) Autoregressive conditional heteroskedasticity (ARCH) Vector autoregression (VAR)
Frequency domain	Spectral density estimation Fourier analysis Wavelet Whittle likelihood

Survival

Survival function	Kaplan–Meier estimator (product limit) Proportional hazards models Accelerated failure time (AFT) model First hitting time
Hazard function	Nelson–Aalen estimator
Test	Log-rank test

Applications

Biostatistics	Bioinformatics Clinical trials / studies Epidemiology Medical statistics
Engineering statistics	Chemometrics Methods engineering Probabilistic design Process / quality control Reliability System identification
Social statistics	Actuarial science Census Crime statistics Demography Econometrics Jurimetrics National accounts Official statistics Population statistics Psychometrics
Spatial statistics	رسم الخرائط Environmental statistics Geographic information system Geostatistics Kriging

Category
خطأ لوا في وحدة:Portal-inline على السطر 80: attempt to call upvalue 'processPortalArgs' (a nil value).
Commons
WikiProject

المربعات الأقل وتحليل الانكفاء

احصاءات حاسوبية

Least squares • المربعات الأقل الخطية • المربعات الأقل الغير خطية • Iteratively reweighted least squares

Correlation and dependence

Pearson product-moment correlation • Rank correlation (Spearman's rho, Kendall's tau) • Partial correlation • Confounding variable

تحليل الانكفاء

Ordinary least squares • Partial least squares • اجمالي المربعات الأقل • Ridge regression

الانكفاء
كنموذج احصائي

انكفاء خطي	انكفاء خطي بسيط • Ordinary least squares • Generalized المربعات الأقل • Weighted least squares • General linear model
البنية المتوقعة	Polynomial regression • Growth curve • Segmented regression • Local regression
غير قياسي	انكفاء غير خطي • Nonparametric • Semiparametric • Robust • Quantile • Isotonic
أخطاء غير طبيعية	Generalized linear model • Binomial • Poisson • Logistic