تحليل عنقودي
التحليل العنقودي Cluster analysis أو التعنقد clustering هي مهمة تجميع مجموعة من المواضيع بطريقة تجعل المواضيع الموجودة في نفس المجموعة (تسمى عنقود) أكثر تشابهًا (بمعنى ما) مع بعضها البعض عن تلك الموجودة في مجموعات أخرى (كتل). إنها مهمة استكشافية للتنقيب عن البيانات، وهي تقنية شائعة لـ تحليل عنقودي لمحلل البيانات الإحصائي، والتي تُستخدم في العديد من المجالات، بما في ذلك إدراك الأنماط، تحليل الصورة ، استرجاع المعلومات، المعلوماتية الحيوية، ضغط البيانات، رسومات الحاسب و التعلم الآلي.
لا يُعتبر التحليل العنقودي في حد ذاته خوارزمية واحدة محددة، ولكنه المهمة العامة التي يتعين حلها. يمكن تحقيقه من خلال خوارزميات مختلفة تختلف اختلافًا كبيرًا في فهمها لما يشكل الكتلة العنقودية وكيفية العثور عليها بكفاءة. تتضمن المفاهيم الشائعة للعناقيد المجموعات ذات المسافات الصغيرة بين أعضاء الكتلة العنقودية، أو المناطق الكثيفة من مساحة البيانات، أو الفواصل الزمنية أو التوزيع الإحصائي. لذلك يمكن صياغة التعنقد كمسألة تحسين متعدد الأهداف. تعتمد خوارزمية التعنقد المناسبة وإعدادات الپارامترات (بما في ذلك الپارامترات مثل استخدام تابع المسافة، أو حد الكثافة أو عدد العناقيد المتوقعة) على مجموعة البيانات الفردية والاستخدام المراد من النتائج. فالتحليل العنقودي على هذا النحو ليس مهمة تلقائية، ولكنه عملية تكرارية لاكتشاف المعرفة أو التحسين التفاعلي متعدد الأهداف الذي يتضمن التجربة والفشل. غالبًا ما يكون من الضروري تعديل المعالجة المسبقة للبيانات وپارامترات النموذج حتى تحقق النتيجة الخصائص المطلوبة.
إلى جانب المصطلح التعنقد ، هناك عدد من المصطلحات ذات المعاني المتشابهة، بما في ذلك التصنيف التلقائي، التصنيف العددي، علم النبات (من اليونانية βότρυς العنب) و التحليل النمطي و اكتشاف المجتمع. غالبًا ما تكون الاختلافات الدقيقة في استخدام النتائج: بينما في التنقيب عن البيانات، تكون المجموعات الناتجة هي موضع الاهتمام، أما في التصنيف التلقائي، تكون للقوة التمييزية الناتجة كل الأهمية.
نشأ التحليل العنقودي في الأنثروپولوجيا بواسطة درايڤر وكروبر في عام 1932[1] وقدم إلى علم النفس من قبل جوزيف زوبين في عام 1938[2] وروبرت تيرون في عام 1939[3] واشتهر باستخدامه من قِبل كاتِل ابتداء من عام 1943[4] لتصنيف نظرية التصنيفات في علم نفس الشخصية.
تعريف
لا يمكن تعريف مفهوم "الكتلة العنقودية" بدقة، وهذا أحد أسباب وجود العديد من خوارزميات التعنقد.[5]هناك قاسم مشترك: مجموعة من مواضيع البيانات. ومع ذلك، يستخدم باحثون مختلفون نماذج عنقودية مختلفة، ويمكن مرة أخرى إعطاء خوارزميات مختلفة لكل من هذه النماذج العنقودية. يختلف مفهوم الكتلة العنقودية، كما وجدته خوارزميات مختلفة، بشكل كبير في خصائصه. إن فهم هذه "النماذج العنقودية" هو المفتاح لفهم الاختلافات بين الخوارزميات المختلفة. تشمل نماذج المجموعات النموذجية ما يلي:
- نماذج الاتصال:على سبيل المثال، يبني التعنقد الهرمي نماذج تعتمد على الاتصال عن بعد.
- نماذج التمركز: على سبيل المثال، تمثل خوارزمية وسائط-k كل كتلة عنقودية بواسطة متجه متوسط واحد.
- نماذج التوزيع: يتم نمذجة الكتل العنقودية باستخدام التوزيعات الإحصائية، مثل التوزيع الطبيعي متعدد المتغيرات المستخدمة بواسطة خوارزمية تعظيم التوقع.
- نماذج الكثافة: على سبيل المثال، يعرّف DBSCAN و OPTICS الكتل العنقودية على أنها مناطق كثيفة متصلة في مساحة البيانات.
- نماذج الفضاء الجزئي:في التعنقد الثنائي (المعروف أيضًا باسم التعنقد المشترك أو التعنقد ثنائي النمط)، يتم نمذجة الكتل العنقودية باستخدام كل من أعضاء الكتلة العنقودية والسمات ذات الصلة.
- نماذج المجموعات: لا تقدم بعض الخوارزميات نموذجًا دقيقًا لنتائجها وتوفر فقط معلومات التجميع.
- النماذج القائمة على الرسم البياني: الزمرة، أي مجموعة فرعية من العقد في الرسم البياني بحيث يمكن اعتبار كل عقدتين في المجموعة الفرعية متصلة بواسطة حافة شكل نموذجي للعنقود. تُعرف عمليات تسهيل متطلبات الاتصال الكاملة (يمكن أن يكون جزء من الحواف مفقودًا) باسم شبه الزمر، كما هو الحال في خوارزمية تعنقد HCS.
- نماذج الرسوم البيانية المؤشرة: كل مسار في رسم بياني مؤشر له علامة من ناتج العلامات الموجودة على الحواف. في ظل افتراضات نظرية التوازن، قد تغير الحواف الإشارة وتؤدي إلى رسم بياني متفرع. "مُسلَّمة القابلية للتعنقد" الأضعف (لا توجد دورة لها حافة سلبية واحدة تماماً) ينتج عنها نتائج بأكثر من مجموعتين عنقوديتين، أو رسوم بيانية فرعية ذات حواف موجبة فقط.[6]
- نماذج عصبونية: أشهر الشبكات العصبونية غير الخاضعة للإشراف هي خريطة التنظيم الذاتي ويمكن وصف هذه النماذج عادةً بأنها مشابهة لواحد أو أكثر من النماذج المذكورة أعلاه، بما في ذلك نماذج الفضاء الجزئي عندما تنفذ الشبكات العصبية شكلاً من تحليل المكونات الرئيسية أو تحليل المكونات المستقلة.
"التعنقد" هو في الأساس مجموعة من هذه المجموعات العنقودية، تحتوي عادةً على جميع المواضيع في مجموعة البيانات. بالإضافة إلى ذلك، قد تحدد علاقة المجموعات ببعضها البعض، على سبيل المثال، التسلسل الهرمي للعناقيد المتضمنة في بعضها البعض. يمكن تمييز المجموعات العنقودية تقريبًا على النحو التالي:
- التعنقد الصارم: ينتمي كل موضوع إلى كتلة عنقودية أو لا
- التعنقد اللين (و أيضاً: التعنقد الضبابي): كل موضوع ينتمي إلى كل مجموعة عنقودية إلى درجة معينة (على سبيل المثال، احتمال الانتماء إلى الكتلة العنقودية)
توجد أيضًا اختلافات محتملة أدق، على سبيل المثال:
- التقسيم العنقودي الصارم: ينتمي كل موضوع إلى مجموعة واحدة فقط
- التقسيم العنقودي الصارم مع القيم المتطرفة: لا يمكن أن تنتمي المواضيع أيضًا إلى أي مجموعة عنقودية، ويتم الأخذ بعين الاعتبار القيم المتطرفة
- التعنقد المتشابك (وأيضاً: التعنقد البديل، التعنقد متعدد الملاحظات): قد تنتمي المواضيع إلى أكثر من مجموعة واحدة؛ عادةً ما تنطوي على مجموعات العنقودية الصارمة
- التعنقد الهرمي: المواضيع التي تنتمي إلى الكتلة العنقودية الفرعية تنتمي أيضًا إلى الكتلة العنقودية الأصل
- تعنقد الفضاء الجزئي: بينما تتم عملية التعنقد المتداخل، داخل فضاء فرعي محدد بشكل فريد، لا يُتوقع أن تقوم المجموعات العنقودية بالتداخل
خوارزميات
كما هو مذكور أعلاه، يمكن تصنيف خوارزميات التعنقد بناءً على نموذج العنقود الخاص بها. ستدرج النظرة العامة التالية فقط لأبرز الأمثلة على خوارزميات التعنقد، حيث من المحتمل أن يكون هناك أكثر من 100 خوارزمية تعنقد منشورة. لا تقدم جميعها نماذج لعناقيدها وبالتالي لا يمكن تصنيفها بسهولة. يمكن العثور على نظرة عامة حول الخوارزميات الموضحة في ويكيپيديا (لموسوعة) في قائمة خوارزميات الإحصاء.
لا توجد خوارزمية تعنقد "صحيحة" بشكل موضوعي، ولكن كما لوحظ، "التعنقد في عين الناظر."[5] غالبًا ما يلزم اختيار خوارزمية التعنقد الأنسب لمسألة معينة بشكل تجريبي، ما لم يكن هناك سبب رياضي لتفضيل نموذج عنقودي على آخر. ستفشل الخوارزمية المصممة لنوع واحد من النماذج عمومًا في مجموعة بيانات تحتوي على نوع مختلف جذريًا من النماذج.[5] على سبيل المثال، لا يمكن للوسائل-k العثور على عناقيد غير محدبة.[5]
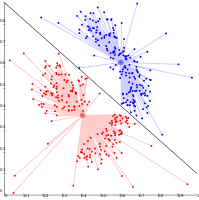
التعنقد القائم على الاتصال (التعنقد الهرمي)
يعتمد التعنقد القائم على الاتصال، والمعروف أيضًا باسم التعنقد الهرمي، على الفكرة الأساسية المتمثلة في أن المواضيع أكثر ارتباطًا بالمواضيع القريبة منها بالأشياء البعيدة. تربط هذه الخوارزميات "المواضيع" لتشكيل "عناقيد" بناءً على المسافة بينها. يمكن وصف الكتلة العنقودية إلى حد كبير بالمسافة القصوى اللازمة لتوصيل أجزاء من الكتلة. على مسافات مختلفة، ستتشكل عناقيد مختلفة، والتي يمكن تمثيلها باستخدام مخطط الشجرة، والذي يشرح من أين يأتي الاسم الشائع "التعنقد الهرمية": لا توفر هذه الخوارزميات تقسيمًا واحدًا لمجموعة البيانات، ولكنها توفر بدلاً من ذلك تسلسل هرمي واسع النطاق من المجموعات العنقودية التي تندمج مع بعضها البعض على مسافات معينة. في مخطط الشجرة، يشير المحور y إلى المسافة التي تندمج عندها المجموعات العنقودية، بينما يتم وضع المواضيع على طول المحور x بحيث لا تختلط هذه المجموعات العنقودية.
التعنقد القائم على الاتصال هو مجموعة كاملة من الأساليب التي تختلف حسب طريقة حساب المسافات. بصرف النظر عن الاختيار المعتاد لـ توابع المسافة، يحتاج المستخدم أيضًا إلى اتخاذ قرار بشأن معيار الربط (نظرًا لأن العنقود يتكون من مواضيع متعددة، فهناك عدة ترشيحات لحساب المسافة) لاستخدامها. تُعرف الاختيارات الشائعة باسم تعنقد أحادي الترابط (الحد الأدنى لمسافات الموضوع)، و تعنقد الترابط الكامل (أقصى مسافات الموضوع)، و UPGMA أو WPGMA (" طريقة مجموعة الأزواج غير الموزونة أو الموزونة بمتوسط حسابي"، تُعرف أيضًا باسم متوسط نعنقد الارتباط). علاوة على ذلك، يمكن أن يكون التعنقد الهرمي تكتليًا (بدءًا من العناصر الفردية وتجميعها في عناقيد) أو تقسيمًا (بدءًا من مجموعة البيانات الكاملة وتقسيمها إلى أقسام).
لن تنتج هذه الطرق تقسيمًا فريدًا لمجموعة البيانات، ولكن التسلسل الهرمي الذي لا يزال المستخدم بحاجة إلى اختيار مجموعات عنقودية مناسبة منه. فهي ليست قوية جدًا تجاه القيم المتطرفة، والتي إما ستظهر كمجموعات عنقودية إضافية أو حتى تتسبب في اندماج مجموعات أخرى (تُعرف باسم "ظاهرة التسلسل"، على وجه الخصوص مع التعنقد أحادي الترابط). في الحالة العامة، يكون التعقيد من أجل التعنقد التكتلي و من أجل التعنقد المقسم،[7]مما يجعلها بطيئة جدًا بالنسبة لمجموعات البيانات الكبيرة. بالنسبة لبعض الحالات الخاصة، تُعرف الأساليب الفعالة المثلى (ذات التعقيد ) : SLINK[8] لربط واحد CLINK[9] لتعنقد الترابط الكامل. في تنظيم استخراج البيانات يتم التعرف على هذه الأساليب كأساس نظري لتحليل الكتلة، ولكنها غالبًا ما تعتبر قديمة[بحاجة لمصدر]. ومع ذلك، فقد قدموا مصدر إلهام للعديد من الأساليب اللاحقة مثل التعنقد على أساس الكثافة.
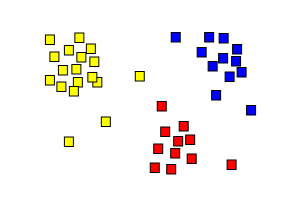
- Linkage clustering examples
التعنقد القائم على النقطة الوسطى
في التعنقد القائم على النقطه الوسطى، يتم تمثيل المجموعات العنقودية بواسطة متجه مركزي، والذي قد لا يكون بالضرورة عنصراً في مجموعة البيانات. عندما يكون عدد المجموعات ثابتًا على k ، فإن تعنقد أوساط k يعطي تعريفًا اصطلاحياً كمسألة تحسين: ابحث عن مراكز المجموعة 'k' و قم بتعيين المواضيع إلى أقرب مركز كتلة، بحيث يتم تقليل المسافات المربعة من الكتلة.
من المعروف أن مسألة التحسين نفسها هي NP-hard، وبالتالي فإن الطريقة الشائعة هي البحث فقط عن حلول تقريبية. الطريقة التقريبية المعروفة بشكل خاص هي خوارزمية إل لويد ،[10]غالبًا ما يشار إليها باسم "خوارزمية أوساط k" (على الرغم من أن خوارزمية أخرى قدمت هذا الاسم). ومع ذلك، فإنه لا يجد سوى الأمثل المحلي، ويتم تشغيله عادة عدة مرات بتهيئة عشوائية مختلفة. غالبًا ما تتضمن الاختلافات في أوساط k مثل هذه التحسينات مثل اختيار أفضل عمليات التشغيل المتعددة، ولكنها تقصر أيضًا النقط الوسطى على عناصر مجموعة البيانات ( متوسطات k)، اختيار متوسطات (تعنقد متوسطات k)، اختيار المراكز الأولية بشكل أقل عشوائية (أوساط k++) أو السماح بتعيين مجموعة عنقودية ضبابية (أوساط c الضبابية).
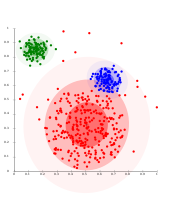
تتطلب معظم خوارزميات النوع أوساط "k" تحديد عدد المجموعات العنقودية مسبقاً، والتي تعتبر واحدة من أكبر عيوب هذه الخوارزميات. علاوة على ذلك، تفضل الخوارزميات مجموعات العنقودية من نفس الحجم تقريبًا، حيث ستقوم دائمًا بتعيين موضوع لأقرب نقطة مركزية. يؤدي هذا غالبًا إلى قطع حدود المجموعات العنقودية بشكل غير صحيح (وهذا ليس مفاجئًا لأن الخوارزمية تعمل على تحسين مراكز المجموعات العنقودية، وليس حدود المجموعة العنقودية).
تمتلك أوساط k عددًا من الخصائص النظرية المثيرة للاهتمام. أولاً، يقسم مساحة البيانات إلى هيكل يُعرف باسم مخطط ڤورونوي. ثانيًا، إنه قريب من الناحية المفاهيمية من تصنيف أقرب المجاورات، وبالتالي فهو شائع في التعلم الآلي. ثالثًا ، يمكن اعتباره تباينًا في التعنقد المستند إلى النموذج، وخوارزمية إل لويد كتنوع في خوارزمية تعظيم التوقعات لهذا النموذج الذي تمت مناقشته أدناه.
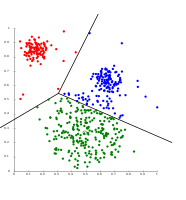
- k-means clustering examples
مشاكل التعنقد المبنية على النقاط الوسطى مثل أوساط k ومتوسطات k هي حالات خاصة من مشكلة موقع العمل، وهي مشكلة أساسية في بحوث العمليات ومجتمعات الهندسة الحسابية. في مشكلة موقع العمل الأساسية (التي يوجد منها العديد من المتغيرات التي تمثل إعدادات أكثر تفصيلاً)، تتمثل المهمة في العثور على أفضل مواقع التخزينات لتقديم الخدمة المثلى لمجموعة معينة من المستهلكات. يمكن للمرء أن ينظر إلى "التخزينات" على أنها نقاط مركزية عنقودية و "مواقع مستهلكات" على أنها البيانات التي سيتم عنقدتها. هذا يجعل من الممكن تطبيق الحلول الخوارزمية المطورة جيدًا من منشورات موقع العمل إلى مشكلة التعنقد القائمة على النقط الوسطى المدروسة حاليًا.
التعنقد القائم على التوزيع
يعتمد نموذج التعنقد الأكثر ارتباطًا بالإحصاءات على نماذج التوزيع. يمكن بعد ذلك تعريف الكتل العنقودية بسهولة على أنها مواضيع تنتمي على الأرجح إلى نفس التوزيع. من الخصائص الملائمة لهذا النهج أنه يشبه إلى حد كبير طريقة إنشاء مجموعات البيانات الاصطناعية: عن طريق أخذ عينات من المواضيع العشوائية من التوزيع.
في حين يكون الأساس النظري لهذه الأساليب متقناً، إلا أنه يعاني من مشكلة رئيسية واحدة تعرف باسم الزيادة، ما لم يتم وضع قيود على تعقيد النموذج. عادةً ما يكون النموذج الأكثر تعقيدًا قادرًا على شرح البيانات بشكل أفضل ، مما يجعل اختيار تعقيد النموذج المناسب أمرًا صعبًا بطبيعته.
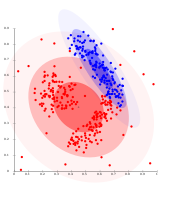
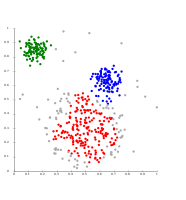
تُعرف إحدى الطرق البارزة بنماذج المزيج الگاوسي (باستخدام خوارزمية تعظيم التوقع). هنا، عادةً ما يتم نمذجة مجموعة البيانات برقم ثابت (لتجنب فرط التخصيص) من التوزيعات الگاوسية الذي تمت تهيئته عشوائيًا والذي تم تحسين پارمتراته بشكل متكرر لتلائم مجموعة البيانات بشكل أفضل. سيتقارب هذا إلى الأمثل المحلي، لذلك قد ينتج عن عمليات التشغيل المتعددة نتائج مختلفة. من أجل الحصول على كتلة عنقودية صلبة، غالبًا ما يتم تعيين المواضيع بعد ذلك إلى التوزيع الگوسي الذي تنتمي إليه على الأرجح؛ للتعنقدات المعتدلة، هذا ليس ضروريًا.
ينتج التعنقد القائم على التوزيع نماذج معقدة للكتل العنقودية التي يمكنها التقاط الارتباط والاعتماد بين السمات. ومع ذلك، تضع هذه الخوارزميات عبئًا إضافيًا على المستخدم: بالنسبة للعديد من مجموعات البيانات الحقيقية، قد لا يكون هناك نموذج رياضي محدد بدقة (على سبيل المثال، افتراض أن التوزيعات الغاوسية هي افتراض قوي إلى حد ما على البيانات).
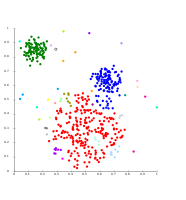
- Gaussian mixture model clustering examples
التعنقد على أساس الكثافة
في التعنقد القائم على الكثافة،[11] يتم تعريف المجموعات العنقودية على أنها مناطق ذات كثافة أعلى من باقي مجموعة البيانات. عادةً ما تُعتبر المواضيع الموجودة في مناطق متفرقة - المطلوبة لفصل المجموعات العنقودية - بمثابة ضجيج ونقاط حدودية. أكثر طرق[12]التعنقد النعتمدة على الكثافة شيوعاً هي DBSCAN.[13]على عكس العديد من الطرق الأحدث، فإنه يتميز بنموذج عنقودي محدد جيدًا يسمى "قابلية الوصول للكثافة". على غرار التعنقد القائم على الترابط، فإنه يعتمد على نقاط الاتصال ضمن حدود مسافة معينة. ومع ذلك، فإنه يربط فقط النقاط التي تفي بمعيار الكثافة، في المتغير الأصلي المحدد على أنه الحد الأدنى لعدد المواضيع الأخرى داخل هذا الشعاع. يتكون التجمع من جميع المواضيع المرتبطة بالكثافة (والتي يمكن أن تشكل مجموعة من شكل عشوائي، على عكس العديد من الطرق الأخرى) بالإضافة إلى جميع المواضيع الموجودة ضمن نطاق هذه المواضيع. خاصية أخرى مثيرة للاهتمام لـ DBSCAN هي أن تعقيدها منخفض إلى حد ما - يتطلب عددًا خطيًا من استعلامات النطاق في قاعدة البيانات - وأنه سيكتشف نفس النتائج بشكل أساسي (فهي حتمية للنقاط الأساسية والضجيج، ولكن ليس للنقاط الحدودية) في كل شوط، لذلك ليست هناك حاجة لتشغيله عدة مرات. OPTICS[14] هو تعميم DBSCAN الذي يلغي الحاجة إلى اختيار قيمة مناسبة لپارامتر النطاق ، ويقدم نتيجة هرمية تتعلق بنتيجة تعنقد الترابط. ديلي كلو،[15]يجمع تعنقد ترابط الكثافة خططاً من تعنقد ترابط واحد و OPTICS، مما يلغي پارامتر تمامًا ويقدم تحسينات في الأداء عبر OPTICS باستخدام فهرس R-tree.
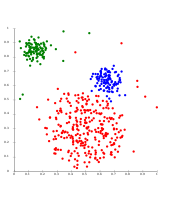
يتمثل العيب الرئيسي في DBSCAN و OPTICS في أنهم يتوقعون نوعًا من انخفاض الكثافة لاكتشاف حدود الكتلة. في مجموعات البيانات ذات التوزيعات الگاوسية المتداخلة على سبيل المثال - حالة استخدام شائعة في البيانات الاصطناعية - غالبًا ما تبدو حدود الكتلة العنقودية التي تنتجها هذه الخوارزميات عشوائية، لأن كثافة الكتلة العنقودية تتناقص باستمرار. على مجموعة البيانات التي تتكون من خليط من گاوسيات، فإن هذه الخوارزميات دائمًا ما تتفوق عليها طرق مثل تعنقد EM التي تكون قادرة على نمذجة هذا النوع من البيانات بدقة.
إزاحة الوسط عبار عن نهج تعنقد حيث يتم نقل كل موضوع إلى المنطقة الأكثر كثافة في جواره، بناءً على تقدير كثافة النواة. في النهاية، تتقارب الأجسام مع الحد الأقصى للكثافة المحلية. على غرار تجميع أوساط k، يمكن أن تعمل "جاذبات الكثافة" هذه كممثلين لمجموعة البيانات، ولكن يمكن أن يكتشف إزاحة الوسط مجموعات عشوائية الشكل مشابهة لـ DBSCAN. نظرًا للإجراء التكراري المكلف وتقدير الكثافة، يكون إزاحة الوسطل عادةً أبطأ من DBSCAN أو أوساط k. بالإضافة إلى ذلك، فإن إمكانية تطبيق خوارزمية إزاحة الوسط على البيانات متعددة الأبعاد يعوقها السلوك غير السلس لتقدير كثافة النواة، مما يؤدي إلى تجزئة نهايات المجموعة بشكل مفرط.[15]
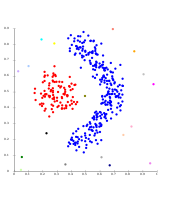
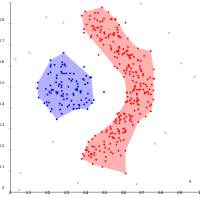
- Density-based clustering examples
التعنقد على أساس الكثافة باستخدام DBSCAN.
تفترض DBSCAN كتل عنقودية متشابهة الكثافة، وقد تواجه مشكلات في فصل العناقيد المجاورة
OPTICS هو متغير DBSCAN، يقوم بتحسين التعامل مع عناقيد الكثافات المختلفة
التعنقد القائم على أساس الشبكة
تُستخدم التقنية القائمة على الشبكة لمجموعة بيانات متعددة الأبعاد.[16] في هذه التقنية، نقوم بإنشاء هيكل شبكي، ويتم إجراء المقارنة على الشبكات (المعروفة أيضًا باسم الخلايا). التقنية القائمة على الشبكة سريعة ولها تعقيد حسابي منخفض. هناك نوعان من طرق التعنقد المستندة إلى الشبكة: STING و CLIQUE. الخطوات المتضمنة في الخوارزمية التعنقد الشبكي هي:
- قسّم مساحة البيانات إلى عدد محدود من الخلايا.
- حدد خلية ’c‘ بشكل عشوائي، حيث لا يجب اجتياز c مسبقًا.
- احسب كثافة ’c‘.
- إذا كانت كثافة ’c‘ أكبر من كثافة العتبة
- وضع علامة على الخلية ’c‘ ككتلة عنقودية جديدة
- حساب كثافة جميع مجاورات ’c‘
- إذا كانت كثافة خلية مجاورة أكبر من كثافة العتبة، فقم بإضافة الخلية في الكتلة العنقودية وكرر الخطوتين 4.2 و 4.3 بحيث لا يوجد مجاور بكثافة أكبر من كثافة العتبة.
- كرر الخطوات 2 و 3 و 4 حتى يتم اجتياز جميع الخلايا.
- توقف.
التطورات الأخيرة
في السنوات الأخيرة ، تم بذل جهود كبيرة لتحسين أداء الخوارزميات الموجودة.[17][18] من بينهم كلارانس (إن جي وهان، 1994) ،[19]و " بيرش" (تشانگ وآخرون، 1996).[20] مع الحاجة الأخيرة إلى معالجة مجموعات بيانات أكبر وأكبر (المعروفة أيضًا باسم البيانات الضخمة) ، فإن الرغبة في تداول المعنى الدلالي للمجموعات العنقودية المولدة للأداء آخذ في الازدياد. أدى ذلك إلى تطوير طرق ما قبل التعنقد مثل تعنقد القبة، والتي يمكنها معالجة مجموعات البيانات الضخمة بكفاءة، ولكن "العناقيد" الناتجة هي مجرد تقسيم أولي لمجموعة البيانات إلى تحليل الأقسام بالطرق الأبطأ الموجودة مثل تعنقد أوساط k.
بالنسبة إلى البيانات عالية الأبعاد، تفشل العديد من الأساليب الحالية بسبب عبء الأبعاد، مما يجعل توابع المسافة الخاصة إشكالية في المساحات عالية الأبعاد. أدى ذلك إلى خوارزميات التعنقد للبيانات عالية الأبعاد التي تركز على تعنقد الفضاء الفرعي (حيث يتم استخدام بعض السمات فقط، وتتضمن نماذج المجموعات السمات ذات الصلة للمجموعة) و تعنقد الارتباط الذي يبحث أيضًا عن مجموعات فضاء جزئية متناوبة عشوائية ("مرتبطة") يمكن نمذجتها بإعطاء ارتباط لسماتها.[21] ومن الأمثلة على خوارزميات التعنقد هذه CLIQUE[22]و SUBCLU.[23]
تم تكييف الأفكار من طرق التعنقد المستندة إلى الكثافة (لا سيما عائلة الخوارزميات DBSCAN / OPTICS) لتعنقد الفضاء الجزئي (HiSC،[24] مجموعات فضاء فرعية هرمية و DiSH[25]) وتعنقد الارتباط (HiCO،[26] تعنقد الارتباط الهرمي، 4C[27] باستخدام "اتصال الارتباط" و ERiC[28]استكشاف مجموعات الارتباط العنقودية الهرمية القائمة على الكثافة).
تم اقتراح العديد من أنظمة التعنقد المختلفة القائمة على المعلومات المتبادلة. أحدهما هو مقياس مارينا ميلو لتباين المعلومات.[29] حيث يزود الآخر التعنقد الهرمي.[30]باستخدام الخوارزميات الجينية، يمكن تحسين مجموعة واسعة من توابع الملاءمة المختلفة، بما في ذلك المعلومات المتبادلة.[31] كما أدى انتشار المُسلَّمات، وهو تطور حديث في علوم الحاسب و الفيزياء الإحصائية، إلى إنشاء أنواع جديدة من خوارزميات التعنقد.[32]
التقييم و التقدير
تقييم (أو "التحقق من صحة") نتائج التعنقد صعب مثل التعنقد نفسه.[33] تتضمن الأساليب الشائعة تقييمًا "داخليًا"، حيث يتم تلخيص التعنقد إلى درجة جودة واحدة، وتقييم "خارجي"، حيث تتم مقارنة التعنقد بتصنيف "الصحة (الحقيقة) الأساسية" الحالي، يتم التقييم المباشر بواسطة خبير بشري، وتقييم "غير مباشر" من خلال تقييم فائدة التعنقد في تطبيقه المقصود.[34]
تعاني مقاييس التقييم الداخلي من المشكلة المتمثلة في أنها تمثل توابع يمكن اعتبارها بحد ذاتها هدفاً عنقودياً. على سبيل المثال، يمكن تعنقد مجموعة البيانات بواسطة معامل سيلويت Silhouette؛ إلا أنه لا توجد خوارزمية فعالة معروفة لهذا الغرض. باستخدام مثل هذا المقياس الداخلي للتقييم، يقارن المرء بدلاً من ذلك تشابه مشاكل التحسين، [34] وليس بالضرورة مدى فائدة المجموعات.
يواجه التقييم الخارجي مشاكل مماثلة: إذا كانت لدينا مثل هذه العلامات "للحقيقة الأساسية"، فلن نحتاج إلى التعنقد؛ وفي التطبيقات العملية ليس لدينا عادة مثل هذه العلامات. من ناحية أخرى، تعكس العلامات فقط تقسيمًا محتملاً واحدًا لمجموعة البيانات العنقودية، وهو ما لا يعني أنه لا توجد مجموعة مختلفة، وربما أفضل.
وبالتالي لا يمكن لأي من هذين النهجين الحكم في النهاية على الجودة الفعلية للتكتل، لكن هذا يحتاج إلى تقييم بشري،[34] وهو أمر غير موضوعي للغاية. ومع ذلك، يمكن أن تكون هذه الإحصاءات مفيدة للغاية في تحديد التجمعات الغير مفيدة،[35] ولكن لا ينبغي لأحد أن يتجاهل التقييم البشري الذاتي (المنطقي).[35]
التقييم الداخلي
عندما يتم تقييم نتيجة التعنقد بناءً على البيانات التي تم تجميعها بنفسها، فإن هذا يسمى التقييم الداخلي. عادةً ما تقوم هذه الطرق بتعيين أفضل درجة للخوارزمية التي تنتج مجموعات عنقودية ذات تشابه كبير داخل الكتلة والتشابه المنخفض بين المجموعات. أحد عيوب استخدام المعايير الداخلية في تقييم الكتلة هو أن الدرجات العالية في مقياس داخلي لا تؤدي بالضرورة إلى تطبيقات فعالة لاسترجاع المعلومات.[36]بالإضافة إلى ذلك، فإن هذا التقييم منحاز نحو الخوارزميات التي تستخدم نفس نموذج الكتلة. على سبيل المثال، يؤدي تعنقد أوساط k بشكل طبيعي إلى تحسين مسافات الموضوع، ومن المحتمل أن يبالغ المعيار الداخلي القائم على المسافة في التعنقد الناتج.
لذلك، فإن مقاييس التقييم الداخلي هي الأنسب للحصول على نظرة ثاقبة في المواقف التي تؤدي فيها إحدى الخوارزميات أداءً أفضل من الأخرى، ولكن هذا لا يعني أن إحدى الخوارزميات تنتج نتائج صحيحة أكثر من غيرها..[5]تعتمد الصلاحية التي يتم قياسها بواسطة مثل هذا المؤشر على الادعاء بوجود هذا النوع من البنية في مجموعة البيانات. لا توجد فرصة لخوارزمية مصممة لنوع من النماذج إذا كانت مجموعة البيانات تحتوي على مجموعة مختلفة جذريًا من النماذج، أو إذا كان التقييم يقيس معيارًا مختلفًا تمامًا.[5] على سبيل المثال، يمكن لتجميع أوساط k العثور على مجموعات عنقودية محدبة فقط، وتفترض العديد من مؤشرات التقييم مجموعات عنقودية محدبة. في مجموعة البيانات التي تحتوي على مجموعات عنقودية غير محدبة، لا يكون استخدام أوساط "k"، ولا مؤشر التقييم الذي يفترض التحدب، سليمًا.
يوجد أكثر من دزينة من إجراءات التقييم الداخلي، والتي تستند عادةً إلى الحدس القائل بأن العناصر الموجودة في نفس المجموعة العنقودية يجب أن تكون أكثر تشابهًا من العناصر الموجودة في مجموعات عنقودية مختلفة.[37] على سبيل المثال، يمكن استخدام الطرق التالية لتقييم جودة خوارزميات التعنقد بناءً على معيار داخلي:
- يمكن حساب مؤشر ديڤس بولدن بالصيغة التالية:
- حيث n هو عدد المجموعات العنقودية، هو نقطة وسطى المجموعة العنقودية ، هو نقطة وسطى المسافة لجميع العناصر في الكتلة العنقودية نقطة وسطى ، و هي المسافة بين نقطتين وسطيتين و .نظرًا لأن الخوارزميات التي تنتج مجموعات عنقودية ذات مسافات منخفضة داخل الكتلة العنقودية (تشابه عالٍ داخل الكتلة العنقودية) ومسافات عالية بين المجموعات (تشابه منخفض بين المجموعات) سيكون لها مؤشر ديڤس بولدن منخفض، خوارزمية التعنقد التي تنتج مجموعة من العناقيد يعتبر أصغر مؤشر ديڤس بولدن أفضل خوارزمية بناءً على هذا المعيار.
- يهدف مؤشر دن إلى تحديد التجمعات العنقودية الكثيفة والمفصولة جيدًا. يتم تعريفه على أنه النسبة بين الحد الأدنى للمسافة بين الكتلة العنقودية إلى أقصى مسافة داخل الكتلة. لكل كتلة عنقودية قسم، يمكن حساب مؤشر دن بالصيغة التالية:[38]
- حيث d(i,j) يمثل المسافة بين المجموعات العنقودية i و j، و d '(k) يقيس المسافة داخل الكتلة العنقودية من الكتلة العنقودية k.المسافة بين الكتلة العنقودية d(i،j) بين مجموعتين عنقوديتين قد يكون أي عدد من مقاييس المسافة، مثل المسافة بين النقطتين الوسطيتين من المجموعات. وبالمثل، يمكن قياس المسافة داخل المجموعة d ( k ) بطرق متنوعة، مثل المسافة القصوى بين أي زوج من العناصر في المجموعة العنقودية k. نظرًا لأن المعيار الداخلي يسعى إلى مجموعات عنقودية ذات تشابه عالٍ داخل المجموعة وتشابه منخفض بين المجموعات العنقودية، فإن الخوارزميات التي تنتج عناقيد ذات مؤشر دن العالي مرغوبة أكثر.
- يتناقض مؤشر رسم البياني بين متوسط المسافة إلى العناصر الموجودة في نفس المجموعة العنقودية مع متوسط المسافة إلى العناصر في المجموعات الأخرى. تعتبر المواضيع ذات قيمة الرسم البياني العالية مجمعة جيدًا، وقد تكون المواضيع ذات القيمة المنخفضة متطرفة. يعمل هذا الفهرس بشكل جيد مع تعنقد أوساط k، ويستخدم أيضًا لتحديد العدد الأمثل للعناقيد.
التقييم الخارجي
في التقييم الخارجي، يتم تقييم نتائج التعنقد بناءً على البيانات التي لم يتم استخدامها للتعنقد، مثل تسميات الفئات المعروفة والمعايير الخارجية. تتكون هذه المعايير من مجموعة من العناصر المصنفة مسبقًا، وغالبًا ما يتم إنشاء هذه المجموعات بواسطة بشر (خبراء). وبالتالي، يمكن اعتبار مجموعات المعايير بمثابة معيار ذهبي للتقييم.[33] تقيس هذه الأنواع من طرق التقييم مدى قرب التعنقد من الفئات المعيارية المحددة مسبقًا. ومع ذلك، فقد نوقش مؤخرًا ما إذا كان هذا مناسبًا للبيانات الحقيقية، أو فقط على مجموعات البيانات التركيبية مع حقيقة أساس واقعية، نظرًا لأن الفئات يمكن أن تحتوي على بنية داخلية، فقد لا تسمح السمات الحالية بفصل المجموعات العنقودية أو قد تحتوي الفئات على الحالات الشاذة.[39] بالإضافة إلى ذلك، من وجهة نظر اكتشاف الإدراك، قد لا يكون نسخ الإدراك المعروف حتماً النتيجة المقصودة.[39] في السيناريو الخاص بالتعنقد المقيّد، حيث يتم استخدام المعلومات الوصفية (مثل تسميات الفئة) بالفعل في عملية التعنقد، ولا يكون الاحتفاظ بالمعلومات عديماً للأهمية لأغراض التقييم.[40]
يتم تكييف عدد من المقاييس من المتغيرات المستخدمة لتقييم مهام التصنيف. بدلاً من حساب عدد المرات التي تم فيها تخصيص فئة بشكل صحيح لنقطة بيانات واحدة (المعروفة باسم إيجابيات صحيحة)، مثلاً تقوم مقاييس "حساب الزوج" بتقييم ما إذا كان كل زوج من نقاط البيانات موجود بالفعل في من المتوقع أن تكون نفس المجموعة العنقودية في نفس الكتلة العنقودية.[33]
كما هو الحال مع التقييم الداخلي، توجد عدة تدابير تقييم خارجية،[37] على سبيل المثال:
- النقاء: النقاء هو مقياس لمدى احتواء المجموعات العنقودية على فئة واحدة.[36] يمكن التفكير في حسابها على النحو التالي: لكل مجموعة، احسب عدد نقاط البيانات من الفئة الأكثر شيوعًا في الكتلة الغنقودية المذكورة. الآن خذ المجموع على كل المجموعات واقسمه على العدد الإجمالي لنقاط البيانات. اصطلاحياً، بالنظر إلى مجموعة من المجموعات وبعض الفئات ، فإن كلا من التقسيم من نقاط البيانات، يمكن تعريف النقاء كما يلي:
- هذا الإجراء لا يمنع من وجود العديد من المجموعات العنقودية. على سبيل المثال، يمكن الحصول على درجة نقاء 1 بوضع كل نقطة بيانات في المجموعة العنقودية الخاصة بها. كما أن النقاء لا يعمل بشكل جيد مع البيانات غير المتوازنة: إذا كان حجم مجموعة البيانات 1000 مكونة من فئتين، تحتوي أحدهما على 999 نقطة والأخرى تحتوي على نقطة واحدة فقط. بغض النظر عن مدى سوء أداء خوارزمية التعنقد، فإنها ستعطي دائمًا قيمة نقاء عالية جدًا.
- يحسب مؤشر راند مدى تشابه المجموعات العنقودية (التي يتم إرجاعها بواسطة خوارزمية التعنقد) مع التصنيفات المعيارية. يمكن للمرء أيضًا عرض مؤشر راند كمقياس للنسبة المئوية للقرارات الصحيحة التي تتخذها الخوارزمية. يمكن حسابها باستخدام الصيغة التالية:
- حيث هو عدد الإيجابيات الصحيحة، هو عدد السلبيات الصحيحة، هو عدد الإيجابيات الخاطئة، و هو عدد السلبيات الخاطئة. إحدى المشكلات المتعلقة بـ مؤشر راند هي أن الإيجابيات الخاطئة والسلبيات الخاطئة موزونة بالتساوي. قد تكون هذه خاصية غير مرغوب فيها لبعض تطبيقات التعنقد. يقوم مقياس F بمعالجة هذا الشأن،[بحاجة لمصدر] كما يفعل مصحح الاحتمال مؤشر راند المعدل.
- يمكن استخدام مقياس F لموازنة مساهمة سلبية خاطئة من خلال ترجيح الاستدعاء من خلال الپارامتر . لنجعل الدقة و الاستدعاء (كلاً من مقاييس التقييم الخارجية في حد ذاتها) حيث يتم تعريفها على النحو التالي:
- حيث هو معدل الدقة و هو معدل الاستدعاء. يمكننا حساب قياس F باستخدام الصيغة التالية:[36]
- عندما ، . بمعنى آخر، ليس ل للاستدعاء أي تأثير على مقياس F عندما ، وازدياد يخصص قدرًا متزايدًا من الوزن ليتم استدعاؤه في مقياس F النهائي.
- أيضاً لا يتم أخذها في الاعتبار ويمكن أن تختلف من 0 إلى أعلى دون قيود.
- يُستخدم مؤشر جاكار لتحديد التشابه بين مجموعتي بيانات. يأخذ مؤشر جاكار قيمة بين 0 و 1. يعني المؤشر 1 أن مجموعتي البيانات متطابقتين، ويشير الفهرس 0 إلى أن مجموعات البيانات لا تحتوي على عناصر مشتركة. يتم تعريف مؤشر جاكار بالصيغة التالية:
- وهذا ببساطة هو عدد العناصر الفريدة المشتركة بين المجموعتين مقسومًا على العدد الإجمالي للعناصر الفريدة في كلتا المجموعتين.
- أيضاً لا يتم أخذها في الاعتبار ويمكن أن تختلف من 0 إلى أعلى دون قيود.
- مقياس دايس المتماثل يضاعف الوزن بينما لا يزال يتم تجاهل :
- مؤشر فولكس مالوز (إي. بي. فولكس وسي. إل. مالوز 1983)[42]
- يحسب مؤشر فولكس مالوز التشابه بين المجموعات العنقودية التي تم إرجاعها بواسطة خوارزمية التعنقد والتصنيفات المعيارية. كلما ارتفعت قيمة مؤشر فولكس مالوز، كلما كانت المجموعات والتصنيفات المرجعية أكثر تشابهًا. يمكن حسابها باستخدام الصيغة التالية:
- حيث هو عدد الإيجابيات الحقيقية، هو عدد الإيجابيات الخاطئة، و هو عدد السلبيات الخاطئة. المؤشر هو الوسط الهندسي لـ دقة و استدعاء و، وبالتالي يُعرف أيضًا باسم مقياس G، بينما مقياس F هو الوسط التوافقي.[43][44]علاوة على ذلك، تعرف الدقة و الاسترجاع أيضًا بمؤشرات والاس و.[45] تتوافق إصدارات الاحتمال المعياري للاستدعاء والدقة وقياس G مع المعرفة و الوضوح و ارتباط ماثيوز وترتبط بشدة بـ كاپا.[46]
- المعلومات المتبادلة هو مقياس نظرية المعلومات لمقدار المعلومات التي يتم مشاركتها بين التعنقد وتصنيف الحقيقة الأساسية الذي يمكنه اكتشاف التشابه غير الخطي بين مجموعتين عنقوديتين. المعلومات المتبادلة الطبيعية هي مجموعة من المتغيرات المصححة احتمالية والتي تحتوي على تحيز أقل لأرقام الكتل العنقودية المتنوعة.[33]
- يمكن استخدام مصفوفة الارتياب لتصور نتائج خوارزمية التصنيف (أو التعنقد) بسرعة. حيث توضح مدى اختلاف الكتلة العنقودية عن الكتلة العنقودية القياسية الذهبية.
اتجاه الكتلة العنقودية
لقياس اتجاه الكتلة العنقودية هو قياس إلى أي درجة توجد الكتل العنقودية في البيانات المراد عنقدتها، ويمكن إجراؤها كاختبار أولي، قبل محاولة القيام بالعنقدة. إحدى طرق القيام بذلك هي مقارنة البيانات بالبيانات العشوائية. في المتوسط، يجب ألا تحتوي البيانات العشوائية على مجموعات عنقودية.
- توجد عدة صيغ لـ إحصائية هوپكنز.[47] منها النموذجية على النحو التالي.[48] لتكن مجموعة من نقطة بيانات في فراغ الأبعاد .لنأخذ بعين الاعتبار عينة عشوائية (بدون استبدال) من نقطة بيانات مع عناصر . لنولد مجموعة من نقطة بيانات موزعة بشكل عشوائي. الآن لنحدد مقياسين للمسافة، لتمون المسافة ل من أقرب مجاور لها في X و لتكون المسافة ل من أقرب مجاور لها في X. نعرف إحصائية هوپكنز كما يلي:
- مع هذا التعريف، يجب أن تميل البيانات العشوائية الموحدة إلى الحصول على قيم قريبة من 0.5، ويجب أن تميل البيانات المعنقدة إلى الحصول على قيم أقرب إلى 1.
- ومع ذلك، فإن البيانات التي تحتوي على گاوسية واحدة فقط ستسجل أيضًا ما يقرب من 1، حيث تقيس هذه الإحصائية الانحراف عن التوزيع الموحد، وليس تعدد الوسائط، مما يجعل هذه الإحصائية عديمة الفائدة إلى حد كبير في التطبيق (بأساس ألا تكون البيانات الحقيقية موحدة عن بعد
على الإطلاق).
تطبيقات
هذا القسم يحتاج المزيد من الأسانيد للتحقق. (November 2016) (Learn how and when to remove this template message) |
علم الأحياء وعلم الأحياء الحسابي والمعلوماتية الحيوية
- نبات و علم بيئة الحيوان
- يستخدم التحليل العنقودي لوصف وإجراء مقارنات مكانية وزمنية لمجتمعات (تجمعات) من الكائنات الحية في بيئات غير متجانسة. يتم استخدامه أيضًا في النظاميات النباتية لتوليد السلالات أو مجموعات من الكائنات الحية (الأفراد) على النوع أو الجنس أو المستوى الأعلى التي تشترك في عدد من السمات.
- ترانسكريپتوميكس
- يستخدم التعنقد لبناء مجموعات عنقودية من الجينات مع أنماط التعبير ذات الصلة (المعروفة أيضًا باسم الجينات المتضافرة) كما في خوارزمية تعنقد HCS.[49][50] غالبًا ما تحتوي هذه المجموعات على بروتينات مرتبطة وظيفيًا، مثل إنزيم من أجل مسار معين، أو جينات منظمة بشكل مشترك. يمكن أن تكون التجارب عالية الإنتاجية باستخدام علامة التسلسل المعبر عنها (ESTs) أو مصفوفة DNA الدقيقة أداة قوية لـ إيضاحات للجينوم - جانب عام من علم الجينوم.
- تحليل السلاسل
- يُستخدم [[تعنقد السلاسل] لتجميع التسلسلات المتماثلة في عائلات الجينات.[51] هذا المفهوم مهم جدًا في المعلوماتية الحيوية و علم الأحياء التطوري بشكل عام. انظر التطور بواسطة تناسخ الجينات.
- منصات التنميط الجيني عالية الإنتاجية
- تُستخدم خوارزميات التعنقد لتعيين الأنماط الجينية تلقائيًا.[52]
- التعنقد الجيني البشري
- يتم استخدام تشابه البيانات الجينية في التعنقد لاستنتاج التركيبات السكانية.
الطب
- التصوير الطبي
- في مسح PET، يمكن استخدام التحليل العنقودي للتمييز بين أنواع مختلفة من الأنسجة في صورة ثلاثية الأبعاد للعديد من الأغراض المختلفة.[53]
- تحليل النشاط المضاد للميكروبات
- يمكن استخدام التحليل العنقودي لتحليل أنماط مقاومة المضادات الحيوية، لتصنيف المركبات المضادة للميكروبات وفقًا لآلية عملها، لتصنيف المضادات الحيوية وفقًا لنشاطها المضاد للبكتيريا.
- تجزئة IMRT
- يمكن استخدام التعنقد لتقسيم خريطة الجسيمات ضمن وحدة مساحة معينة إلى مناطق متميزة لتحويلها إلى مجالات قابلة للتقديم في العلاج الإشعاعي القائم على MLC.
الأعمال والتسويق
- بحث السوق
- يستخدم التحليل العنقودي على نطاق واسع في أبحاث السوق عند العمل مع البيانات متعددة المتغيرات من المسوحات ولوحات الاختبار. يستخدم باحثو السوق التحليل العنقودي لتقسيم الكثافة السكانية العامة لـ مستهلكين في قطاعات السوق وفهم العلاقات بين المجموعات المختلفة من العملاء المستهلكين / المحتملين بشكل أفضل، ولاستخدامها في السوق التجزئة، تحديد موقع المنتج، تطوير منتج جديد واختيار أسواق الاختبار.
- تجميع عناصر التسوق
- يمكن استخدام التعنقد لتجميع جميع عناصر التسوق المتاحة على الويب في مجموعة من المنتجات الفريدة. على سبيل المثال، يمكن تجميع كافة العناصر الموجودة على موقع إي باي eBay في منتجات فريدة (ليس لدى إي باي eBay مفهوم SKU).
شبكة الانترنت
- تحليل الشبكة الاجتماعية
- في دراسة الشبكات الاجتماعية، يمكن استخدام التعنقد للتعرف على المجتمعات داخل مجموعات كبيرة من الأشخاص.
- تجميع نتائج البحث
- في عملية التعنقد الذكي للملفات ومواقع الويب، يمكن استخدام التعنقد لإنشاء مجموعة أكثر صلة من نتائج البحث مقارنة بمحركات البحث العادية مثل گوگل[بحاجة لمصدر].يوجد حاليًا عدد من أدوات التعنقد المستندة إلى الويب مثل الأدوات العنقودية. يمكن استخدامه أيضًا لإرجاع مجموعة أكثر شمولاً من النتائج في الحالات التي قد يشير فيها مصطلح البحث إلى أشياء مختلفة إلى حد كبير. يتوافق كل استخدام مميز للمصطلح مع مجموعة فريدة من النتائج، مما يسمح لخوارزمية الترتيب بإرجاع نتائج شاملة عن طريق اختيار أفضل نتيجة من كل مجموعة عنقودية.[54]
- تحسين الخريطة الزلقة
- تستخدم خريطة الصور ومواقع الخرائط الأخرى الخاصة بـ فليكر التعنقد لتقليل عدد العلامات على الخريطة. هذا يجعله أسرع ويقلل من كمية الفوضى المرئية.
المعلوماتية
- تطور البرمجيات
- يكون التعنقد مفيداً في تطوير البرامج لأنه يساعد على تقليل الخصائص القديمة في التعليمات البرمجية عن طريق إعادة تشكيل التشغسل التي أصبحت مشتتة. فهي شكل من أشكال إعادة الهيكلة وبالتالي فهي طريقة للصيانة الوقائية المباشرة.
- تقسيم الصورة
- يمكن استخدام التعنقد لتقسيم صورة رقمية إلى أقسام متميزة لـ اكتشاف الحدود أو التعرف على الشيء.[55]
- الخوارزميات التطورية
- يمكن استخدام التعنقد لتحديد المجالات المختلفة داخل مجتمع خوارزمية تطورية بحيث يمكن توزيع فرصة التوالد بشكل أكثر توازناً بين الأصناف أو الأنواع الفرعية المتطورة.
- الأنظمة الموصية
- تم تصميم الأنظمة الموصية للتوصية بالعناصر الجديدة بناءً على رغبة المستخدم. حيث يقومون باستخدام خوارزميات التعنقد أحيانًا للتنبؤ بتفضيلات المستخدم بناءً على تفضيلات المستخدمين الآخرين في المجموعة العنقودية للمستخدم.
- أساليب سلسلة ماركوڤ مونت كارلو
- غالبًا ما يتم استخدام التعنقد لتحديد موقع وتوصيف القيم العظمى في التوزيع المستهدف.
- اكتشاف الأخطاء
- يتم تعريف الانحرافات / القيم المتطرفة (الشذوذات) بشكل نموذجي - سواء كان ذلك بشكل صريح أو ضمني - فيما يتعلق ببنية التعنقد في البيانات.
- معالجة اللغة الطبيعية
- يمكن استخدام التعنقد لحل الغموض المفرداتي.[54]
العلوم الإنسانية
- تحليل الجريمة
- يمكن استخدام التحليل العنقودي لتحديد المجالات التي توجد فيها حوادث أكبر لأنواع معينة من الجرائم. من خلال تحديد هذه المناطق المميزة أو "النقاط الساخنة" حيث حدثت جريمة مماثلة على مدى فترة من الزمن، من الممكن إدارة موارد تنفيذ القانون بشكل أكثر فعالية.
- التنقيب عن البيانات التعليمية
- يستخدم التحليل العنقودي على سبيل المثال لتحديد مجموعات المدارس أو الطلاب الذين لديهم مميزات مماثلة.
- الأنماط (الطبولوجيا)
- من بيانات الاستطلاع، تستخدم المشاريع مثل تلك التي يضطلع بها مركز پيو للأبحاث Pew Research Center التحليل العنقودي لتمييز أنماط الآراء والعادات والتركيبة السكانية التي قد تكون مفيدة في السياسة والتسويق.
أمور أخرى
- الروبوتات الميدانية
- تُستخدم خوارزميات التعنقد لإدراك الموقف الآلي لتتبع الأشياء واكتشاف القيم المتطرفة في بيانات المستشعر.[56]
- الكيمياء الرياضية
- للعثور على التشابه الهيكلي، وما إلى ذلك، على سبيل المثال، تم تجميع 3000 مركب كيميائي في مساحة 90 مؤشر طوبولوجي.[57]
- علم المناخ
- للعثور على أنظمة الطقس أو الأنماط الجوية القريبة لضغط مستوى سطح البحر.[58]
- الطاقات المتجددة
- العثور على مناطق مهجورة تصلح لبناء محطات الطاقة الشمسية.[59]
- الموارد المالية
- تم استخدام التحليل العنقودي لتجميع الأسهم في القطاعات.[60]
- جيولوجيا البترول
- يستخدم التحليل العنقودي لإعادة بناء البيانات الأساسية للبئر السفلي المفقودة أو منحنيات السجل المفقودة من أجل تقييم خصائص الاحتياطي.
- الكيمياء الجيولوجية
- للتجميع العنقودي الخواص الكيميائية في مواقع عينات مختلفة.
انظر أيضاً
الأنواع المتخصصة من التحليل العنقودي
- Automatic Clustering Algorithms
- Balanced clustering
- Clustering high-dimensional data
- Conceptual clustering
- Consensus clustering
- Constrained clustering
- Community detection
- Data stream clustering
- HCS clustering
- Sequence clustering
- Spectral clustering
التقنيات المستخدمة في التحليل العنقودي
- Artificial neural network (ANN)
- Nearest neighbor search
- Neighbourhood components analysis
- Latent class analysis
- Affinity propagation
تخطيط البيانات والمعالجة المسبقة
أمور أخرى
- Cluster-weighted modeling
- Curse of dimensionality
- Determining the number of clusters in a data set
- Parallel coordinates
- Structured data analysis
المراجع
- ^ Driver and Kroeber (1932). "Quantitative Expression of Cultural Relationships". University of California Publications in American Archaeology and Ethnology. Quantitative Expression of Cultural Relationships: 211–256 – via http://dpg.lib.berkeley.edu.
{{cite journal}}: External link in|via= - ^ Zubin, Joseph (1938). "A technique for measuring like-mindedness". The Journal of Abnormal and Social Psychology (in الإنجليزية). 33 (4): 508–516. doi:10.1037/h0055441. ISSN 0096-851X.
- ^ Tryon, Robert C. (1939). Cluster Analysis: Correlation Profile and Orthometric (factor) Analysis for the Isolation of Unities in Mind and Personality. Edwards Brothers.
- ^ Cattell, R. B. (1943). "The description of personality: Basic traits resolved into clusters". Journal of Abnormal and Social Psychology. 38 (4): 476–506. doi:10.1037/h0054116.
- ^ أ ب ت ث ج ح Estivill-Castro, Vladimir (20 June 2002). "Why so many clustering algorithms – A Position Paper". ACM SIGKDD Explorations Newsletter. 4 (1): 65–75. doi:10.1145/568574.568575. S2CID 7329935.
- ^ James A. Davis (May 1967) "Clustering and structural balance in graphs", Human Relations 20:181–7
- ^ Everitt, Brian (2011). Cluster analysis. Chichester, West Sussex, U.K: Wiley. ISBN 9780470749913.
- ^ Sibson, R. (1973). "SLINK: an optimally efficient algorithm for the single-link cluster method" (PDF). The Computer Journal. British Computer Society. 16 (1): 30–34. doi:10.1093/comjnl/16.1.30.
- ^ Defays, D. (1977). "An efficient algorithm for a complete link method". The Computer Journal. British Computer Society. 20 (4): 364–366. doi:10.1093/comjnl/20.4.364.
- ^ Lloyd, S. (1982). "Least squares quantization in PCM". IEEE Transactions on Information Theory. 28 (2): 129–137. doi:10.1109/TIT.1982.1056489.
- ^ Kriegel, Hans-Peter; Kröger, Peer; Sander, Jörg; Zimek, Arthur (2011). "Density-based Clustering". WIREs Data Mining and Knowledge Discovery. 1 (3): 231–240. doi:10.1002/widm.30.
- ^ Microsoft academic search: most cited data mining articles Archived 2010-04-21 at the Wayback Machine: DBSCAN is on rank 24, when accessed on: 4/18/2010
- ^ (1996) "A density-based algorithm for discovering clusters in large spatial databases with noise". Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96): 226–231, AAAI Press.
- ^ (1999) "OPTICS: Ordering Points To Identify the Clustering Structure". ACM SIGMOD international conference on Management of data: 49–60, ACM Press.
- ^ أ ب (2006) "Advances in Knowledge Discovery and Data Mining". 3918: 119–128. doi:10.1007/11731139_16.
- ^ Aggarwal, Charu C., editor. Reddy, Chandan K., editor. Data Clustering : Algorithms and Applications. ISBN 978-1-315-37351-5. OCLC 1110589522.
{{cite book}}:|last=has generic name (help)CS1 maint: multiple names: authors list (link) - ^ Sculley, D. (2010). "Web-scale k-means clustering" in Proc. 19th WWW..
- ^ Huang, Z. (1998). "Extensions to the k-means algorithm for clustering large data sets with categorical values". Data Mining and Knowledge Discovery. 2 (3): 283–304. doi:10.1023/A:1009769707641. S2CID 11323096.
- ^ R. Ng and J. Han. "Efficient and effective clustering method for spatial data mining". In: Proceedings of the 20th VLDB Conference, pages 144–155, Santiago, Chile, 1994.
- ^ Tian Zhang, Raghu Ramakrishnan, Miron Livny. "An Efficient Data Clustering Method for Very Large Databases." In: Proc. Int'l Conf. on Management of Data, ACM SIGMOD, pp. 103–114.
- ^ Kriegel, Hans-Peter; Kröger, Peer; Zimek, Arthur (July 2012). "Subspace clustering". Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. 2 (4): 351–364. doi:10.1002/widm.1057.
- ^ Agrawal, R.; Gehrke, J.; Gunopulos, D.; Raghavan, P. (2005). "Automatic Subspace Clustering of High Dimensional Data". Data Mining and Knowledge Discovery. 11: 5–33. CiteSeerX 10.1.1.131.5152. doi:10.1007/s10618-005-1396-1. S2CID 9289572.
- ^ Karin Kailing, Hans-Peter Kriegel and Peer Kröger. Density-Connected Subspace Clustering for High-Dimensional Data. In: Proc. SIAM Int. Conf. on Data Mining (SDM'04), pp. 246–257, 2004.
- ^ (2006) "Knowledge Discovery in Databases: PKDD 2006". 4213: 446–453. doi:10.1007/11871637_42.
- ^ (2007) "Advances in Databases: Concepts, Systems and Applications". 4443: 152–163. doi:10.1007/978-3-540-71703-4_15.
- ^ Achtert, E.; Böhm, C.; Kröger, P.; Zimek, A. (2006). "Mining Hierarchies of Correlation Clusters". Proc. 18th International Conference on Scientific and Statistical Database Management (SSDBM): 119–128. CiteSeerX 10.1.1.707.7872. doi:10.1109/SSDBM.2006.35. ISBN 978-0-7695-2590-7. S2CID 2679909.
- ^ Böhm, C.; Kailing, K.; Kröger, P.; Zimek, A. (2004). "Computing Clusters of Correlation Connected objects". Proceedings of the 2004 ACM SIGMOD international conference on Management of data - SIGMOD '04. p. 455. CiteSeerX 10.1.1.5.1279. doi:10.1145/1007568.1007620. ISBN 978-1581138597. S2CID 6411037.
- ^ Achtert, E.; Bohm, C.; Kriegel, H. P.; Kröger, P.; Zimek, A. (2007). "On Exploring Complex Relationships of Correlation Clusters". 19th International Conference on Scientific and Statistical Database Management (SSDBM 2007). p. 7. CiteSeerX 10.1.1.71.5021. doi:10.1109/SSDBM.2007.21. ISBN 978-0-7695-2868-7. S2CID 1554722.
- ^ Meilă, Marina (2003). "Learning Theory and Kernel Machines". 2777: 173–187. doi:10.1007/978-3-540-45167-9_14.
- ^ Kraskov, Alexander; Stögbauer, Harald; Andrzejak, Ralph G.; Grassberger, Peter (1 December 2003). "Hierarchical Clustering Based on Mutual Information". arXiv:q-bio/0311039. Bibcode:2003q.bio....11039K.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Auffarth, B. (July 18–23, 2010). "Clustering by a Genetic Algorithm with Biased Mutation Operator". Wcci Cec. IEEE.
- ^ Frey, B. J.; Dueck, D. (2007). "Clustering by Passing Messages Between Data Points". Science. 315 (5814): 972–976. Bibcode:2007Sci...315..972F. CiteSeerX 10.1.1.121.3145. doi:10.1126/science.1136800. PMID 17218491. S2CID 6502291.
- ^ أ ب ت ث Pfitzner, Darius; Leibbrandt, Richard; Powers, David (2009). "Characterization and evaluation of similarity measures for pairs of clusterings". Knowledge and Information Systems. Springer. 19 (3): 361–394. doi:10.1007/s10115-008-0150-6. S2CID 6935380.
- ^ أ ب ت Feldman, Ronen; Sanger, James (2007-01-01). The Text Mining Handbook: Advanced Approaches in Analyzing Unstructured Data. Cambridge Univ. Press. ISBN 978-0521836579. OCLC 915286380.
- ^ أ ب Weiss, Sholom M.; Indurkhya, Nitin; Zhang, Tong; Damerau, Fred J. (2005). Text Mining: Predictive Methods for Analyzing Unstructured Information. Springer. ISBN 978-0387954332. OCLC 803401334.
- ^ أ ب ت Manning, Christopher D.; Raghavan, Prabhakar; Schütze, Hinrich (2008-07-07). Introduction to Information Retrieval. Cambridge University Press. ISBN 978-0-521-86571-5.
- ^ أ ب Knowledge Discovery in Databases – Part III – Clustering, Heidelberg University, 2017, https://dbs.ifi.uni-heidelberg.de/files/Team/eschubert/lectures/KDDClusterAnalysis17-screen.pdf
- ^ Dunn, J. (1974). "Well separated clusters and optimal fuzzy partitions". Journal of Cybernetics. 4: 95–104. doi:10.1080/01969727408546059.
- ^ أ ب (2010) "On Using Class-Labels in Evaluation of Clusterings". MultiClust: Discovering, Summarizing, and Using Multiple Clusterings, ACM SIGKDD.
- ^ (2014) "Model Selection for Semi-Supervised Clustering". Proceedings of the 17th International Conference on Extending Database Technology (EDBT): 331–342. doi:10.5441/002/edbt.2014.31.
- ^ Rand, W. M. (1971). "Objective criteria for the evaluation of clustering methods". Journal of the American Statistical Association. American Statistical Association. 66 (336): 846–850. arXiv:1704.01036. doi:10.2307/2284239. JSTOR 2284239.
- ^ Fowlkes, E. B.; Mallows, C. L. (1983). "A Method for Comparing Two Hierarchical Clusterings". Journal of the American Statistical Association. 78 (383): 553–569. doi:10.1080/01621459.1983.10478008. JSTOR 2288117.
- ^ Powers, David (2003). "Recall and Precision versus the Bookmaker" in International Conference on Cognitive Science.: 529–534.
- ^ Arabie, P. (1985). "Comparing partitions". Journal of Classification. 2 (1): 1985. doi:10.1007/BF01908075. S2CID 189915041.
- ^ Wallace, D. L. (1983). "Comment". Journal of the American Statistical Association. 78 (383): 569–579. doi:10.1080/01621459.1983.10478009.
- ^ (2012) "The Problem with Kappa" in European Chapter of the Association for Computational Linguistics.: 345–355.
- ^ Hopkins, Brian; Skellam, John Gordon (1954). "A new method for determining the type of distribution of plant individuals". Annals of Botany. Annals Botany Co. 18 (2): 213–227. doi:10.1093/oxfordjournals.aob.a083391.
- ^ Banerjee, A. (2004). "Validating clusters using the Hopkins statistic". IEEE International Conference on Fuzzy Systems. 1: 149–153. doi:10.1109/FUZZY.2004.1375706. ISBN 978-0-7803-8353-1. S2CID 36701919.
- ^ Johnson, Stephen C. (1967-09-01). "Hierarchical clustering schemes". Psychometrika (in الإنجليزية). 32 (3): 241–254. doi:10.1007/BF02289588. ISSN 1860-0980. PMID 5234703. S2CID 930698.
- ^ Hartuv, Erez; Shamir, Ron (2000-12-31). "A clustering algorithm based on graph connectivity". Information Processing Letters. 76 (4): 175–181. doi:10.1016/S0020-0190(00)00142-3. ISSN 0020-0190.
- ^ Remm, Maido; Storm, Christian E. V.; Sonnhammer, Erik L. L. (2001-12-14). "Automatic clustering of orthologs and in-paralogs from pairwise species comparisons11Edited by F. Cohen". Journal of Molecular Biology. 314 (5): 1041–1052. doi:10.1006/jmbi.2000.5197. ISSN 0022-2836. PMID 11743721.
- ^ Botstein, David; Cox, David R.; Risch, Neil; Olshen, Richard; Curb, David; Dzau, Victor J.; Chen, Yii-Der I.; Hebert, Joan; Pesich, Robert (2001-07-01). "High-Throughput Genotyping with Single Nucleotide Polymorphisms". Genome Research (in الإنجليزية). 11 (7): 1262–1268. doi:10.1101/gr.157801 (inactive 2020-08-25). ISSN 1088-9051. PMC 311112. PMID 11435409.
{{cite journal}}: CS1 maint: DOI inactive as of أغسطس 2020 (link) - ^ Filipovych, Roman; Resnick, Susan M.; Davatzikos, Christos (2011). "Semi-supervised Cluster Analysis of Imaging Data". NeuroImage. 54 (3): 2185–2197. doi:10.1016/j.neuroimage.2010.09.074. PMC 3008313. PMID 20933091.
- ^ أ ب Di Marco, Antonio; Navigli, Roberto (2013). "Clustering and Diversifying Web Search Results with Graph-Based Word Sense Induction". Computational Linguistics. 39 (3): 709–754. doi:10.1162/COLI_a_00148. S2CID 1775181.
- ^ Bewley, A., & Upcroft, B. (2013). Advantages of Exploiting Projection Structure for Segmenting Dense 3D Point Clouds. In Australian Conference on Robotics and Automation [1]
- ^ Bewley, A.; et al. "Real-time volume estimation of a dragline payload". IEEE International Conference on Robotics and Automation. 2011: 1571–1576.
- ^ Basak, S.C.; Magnuson, V.R.; Niemi, C.J.; Regal, R.R. (1988). "Determining Structural Similarity of Chemicals Using Graph Theoretic Indices". Discr. Appl. Math. 19 (1–3): 17–44. doi:10.1016/0166-218x(88)90004-2.
- ^ Huth, R.; et al. (2008). "Classifications of Atmospheric Circulation Patterns: Recent Advances and Applications". Ann. N.Y. Acad. Sci. 1146: 105–152. Bibcode:2008NYASA1146..105H. doi:10.1196/annals.1446.019. PMID 19076414.
- ^ Franco, D.; Steiner, M. (2018). "Clustering of solar energy facilities using a hybrid fuzzy c-means algorithm initialized by metaheuristics". Journal of Cleaner Production. 191: 445–457. doi:10.1016/j.jclepro.2018.04.207.
- ^ Arnott, Robert D. (1980-11-01). "Cluster Analysis and Stock Price Comovement". Financial Analysts Journal. 36 (6): 56–62. doi:10.2469/faj.v36.n6.56. ISSN 0015-198X.
- CS1 errors: generic name
- CS1 maint: DOI inactive as of أغسطس 2020
- Articles with long short description
- Short description is different from Wikidata
- Articles with hatnote templates targeting a nonexistent page
- Articles with unsourced statements from March 2016
- Articles with unsourced statements from May 2018
- Articles needing additional references from November 2016
- All articles needing additional references
- Articles with unsourced statements from July 2018
- تحليل عنقودي
- Data mining
- Geostatistics