فضاء التمثيل
نظرية التمثيل Representation theory هي فرع من الرياضيات تدرس البنية الجبرية المجردة من خلال تمثيل عناصرها على أنها تحويلات خطية من فضاء المتجهات،[1]ودراسات الوحدات على هذه الهياكل الجبرية المجردة.[2][3] من حيث الجوهر، يجعل التمثيل الكائن الجبري المجرّد أكثر واقعية من خلال وصف عناصره بواسطة المصفوفات و العمليات الجبرية (على سبيل المثال، إضافة مصفوفة، ضرب المصفوفات). إن نظرية المصفوفات والعوامل الخطية مفهومة جيداً، لذا فإن تمثيلات الكائنات الأكثر تجريداً من حيث كائنات الجبر الخطي المألوفة تساعد في جمع الخصائص وأحياناً تبسيط العمليات الحسابية على نظريات أكثر تجريدية.
تتضمن الكائنات الجبرية القابلة لمثل هذا الوصف المجموعات و الجبر الترابطي و جبر لي. أبرزها (والأول تاريخياً) هو نظرية تمثيل المجموعات، حيث يتم تمثيل عناصر المجموعة بمصفوفات عكسية بطريقة تجعل عملية المجموعة هي ضرب المصفوفة.[4][5]
تعتبر نظرية التمثيل طريقة مفيدة لأنها تقلل المشكلات في الجبر المجرد إلى مشاكل في الجبر الخطي، وهو موضوع مفهوم جيداً.[6]علاوة على ذلك، يمكن أن تكون مساحة المتجه التي يتم تمثيل المجموعة عليها (على سبيل المثال) ذات أبعاد لا نهائية، ومن خلال السماح لها أن تكون، على سبيل المثال، فضاء هلبرت، يمكن أن تطبق طرق التحليل على نظرية المجموعات.[7][8]تعتبر نظرية التمثيل مهمة أيضاً في الفيزياء لأنها، على سبيل المثال، تصف كيفية تأثير مجموعة التناظر لنظام مادي في حلول المعادلات التي تصف ذلك النظام.[9]
تنتشر نظرية التمثيل في مجالات الرياضيات لسببين. أولاً، تطبيقات نظرية التمثيل متنوعة:[10]بالإضافة إلى تأثيرها على الجبر، فنظرية التمثيل:
- توضح وتعمم تحليل فورييه عبر التحليل التوافقي،[11]
- متصلة بـ الهندسة عبر النظرية الثابتة و برنامج إرلانگن،[12]
- لها تأثير في نظرية الأعداد من خلال الصيغة الآلية و برنامج لانگلاندس.[13]
ثانياً، هناك مناهج متنوعة لنظرية التمثيل. يمكن دراسة الأشياء نفسها باستخدام طرق من الهندسة الجبرية، نظرية الوحدة، نظرية العدد التحليلي، الهندسة التفاضلية، نظرية المشغل، التوافقية الجبرية و الطوبولوجية.[14]
أدى نجاح نظرية التمثيل إلى العديد من التعميمات. واحدة من أكثرها عمومية في نظرية التصنيف.[15] يمكن النظر إلى الكائنات الجبرية التي تنطبق عليها نظرية التمثيل على أنها أنواع معينة من التصنيفات، والتمثيلات على أنها منفذات من فئة الكائن إلى تصنيف فضاءات المتجهات.[5] يشير هذا الوصف إلى تعميمين واضحين: أولاً، يمكن استبدال الكائنات الجبرية بتصنيفات أكثر عمومية؛ ثانياً، يمكن استبدال التصنيف المستهدف للفضاءات المتجهة بتصنيفات أخرى مفهومة جيداً.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تعاريف و مفاهيم
لنفترض أن V هو فضاء متجه على المجال F.[6]على سبيل المثال، لنفترض V هو Rn أو Cn، وهو الفضاء القياسي ذي الأبعاد n لمتجهات العمود على الأعداد الحقيقية أو المركبة، على التوالي. في هذه الحالة، فكرة نظرية التمثيل هي القيام الجبر المجرد بشكل ملموس باستخدام المصفوفات n × n أرقام حقيقية أو مركبة.
هناك ثلاثة أنواع رئيسية من الكائنات الجبرية يمكن إجراء ذلك من أجل: المجموعات، الجبر الترابطي و تضمين الجبر.[16][5]
- مجموعة جميع المصفوفات القابلة للانعكاس n × n هي مجموعة بحكم ضرب المصفوفة، وتحلل نظرية تمثيل المجموعات من خلال وصف ("تمثيل") عناصرها من حيث المصفوفات القابلة للانعكاس.
- إضافة المصفوفة والضرب يجعلان مجموعة جميع مصفوفات n × n ضمن الجبر الترابطي، وبالتالي هناك نظرية التمثيل للجبر الترابطي.
- إذا استبدلنا ضرب المصفوفة MN بالمصفوفة المبدل MN − NM، ثم n × n؛ تصبح مصفوفات n بدلاً من ذلك عبارة عن جبر لي، مما يؤدي إلى نظرية التمثيل لجبر لي.
يتم تعميم هذه على أي مجال F وعلى أي فضاء متجه V علىF، مع استبدال الخرائط الخطية و التكوين الذي يحل محل مضاعفة المصفوفة: هناك مجموعة GL(V,F) من التشكل الذاتي لـ V، والجبر الترابطي EndFV لجميع الأشكال الداخلية لـ V، وجبر لي المقابل gl(V,F).
تعريف
هناك طريقتان لقول ما هو التمثيل.[17] يستخدم الأول فكرة الإجراء، مع تعميم الطريقة التي تعمل بها المصفوفات على متجهات العمود بضرب المصفوفة. تمثيل مجموعة G أو (ترابطي أو لي) الجبر A على فضاء متجهي V عبارة عن مخطط: مع خاصيتين. أولاً، بالنسبة لأي g في G (أو a في A)، فإن المخطط
خطي (على F). ثانياً، إذا قدمنا الترميز g · v لـ (g, v)، إذاً من أجل أي g1, g2 في G وv في V:
حيث e هو عنصر المطابقة لـG و g1g2 هو الناتج في G. فشرطالجبر الترابطي مشابه، باستثناء أن الجبر الترابطي لا يحتوي دائماً على عنصر مطابقة، وفي هذه الحالة يتم تجاهل المعادلة (1). المعادلة (2) هي تعبير تجريدي عن ترابط ضرب المصفوفة. هذا لا ينطبق على عاكس المصفوفة وأيضاً لا يوجد عنصر مطابقة للمحول. ومن ثم بالنسبة لجبر لي، فإن الشرط الوحيد هو أن أي x1, x2 في A و v في V:
حيث [x1, x2] هو قوس لي، الذي يعمم مبدل المصفوفة MN − NM.
تركز الطريقة الثانية لتحديد التمثيل على المخطط أرسال φ g في G إلى مخطط خطي φ(g): V → V، حيث تحقق
وبالمثل في الحالات الأخرى. هذا النهج أكثر إيجازاً وأكثر تجريداً. من وجهة النظر هذه:
- تمثيل مجموعة G على فضاء متجه V هو تماثل مجموعة φ: G → GL(V,F);[8]
- تمثيل الجبر الترابطي A على فضاء متجه V هو تماثل الجبر φ: A → EndF(V);[8]
- تمثيل جبر لي 𝖆 على فضاء متجه V هو تماثل جبر لي φ: 𝖆 → gl(V,F).
مصطلحات
يسمى فضاء المتجه V فضاء التمثيل لـ φ و البعد (إذا كان محدود) تسمى حجم التمثيل (أحياناً درجة، كما في [18]). ومن التطبيقات الشائعة أيضاً الإشارة إلى V نفسه باعتباره التمثيل عندما يكون التشابه الشكلي φ واضحاً من السياق؛ وبخلاف ذلك، يمكن استخدام الترميز (V،φ) للإشارة إلى التمثيل.
عندما يكون V ذو بعد محدد n، يمكن للمرء اختيار أساس لـV لتحديدV مع Fn، وبالتالي استعادة تمثيل مصفوفة بإدخالات في الحقل F.
التأثير الفعال أو التمثيل الصحيح هو التمثيل ((V،φ)، حيث يكون تماثل الشكل φ إدخالاً.
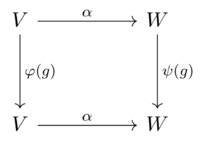
المخططات المكافئة والتماثلات
إذا كانت V و W عبارة عن فضاءات متجهة على F ، ومجهزة بتمثيلات φ و ψ لمجموعة G، ثم المخطط المكافئ من V إلى W هو مخطط خطي α: V → W مثل
لكل g في G و v في V. من ناحية φ: G → GL(V) و ψ: G → GL(W)، هذا يعني
لكل g في G، هذا، الرسم التخطيطي التالي:
يتم تعريف المخططات المكافئة للتمثيلات الترابطية أو الجبر بطريقة مماثلة. إذا كانت α قابلة للعكس، فيُقال إنها تماثل الشكل، وفي هذه الحالة V و W (أو بشكل أكثر دقة، φ و ψ) هي تمثيلات متشابهة، تمت صياغتها أيضاً على أنها "تمثيلات مكافئة". غالباً ما يطلق على المخطط المكافئ اسم مخطط متشابك للتمثيلات. أيضاً، في حالة المجموعة G، يُطلق عليها أحياناً مخطط G.
التمثيلات المتشابهة، لأغراض عملية، "هي نفسها"؛ تقدم نفس المعلومات حول المجموعة أو الجبر الذي يتم تمثيله. لذلك تسعى نظرية التمثيل إلى تصنيف التمثيلات حتى التماثل.
التمثيلات الفرعية، وحواصل القسمة، والتمثيلات غير القابلة للاختزال
إذا هو تمثيل على سبيل المثال لمجموعة ، و هو فضاء فرعي خطي لـ الذي يتم الحفاظ عليه بفعل بمعنى أنه بالنسبة لكل و , (يسمي سير هذه مستقرة بحكم [18])، من ثم يسمى بتمثيل فرعي: بالتعريف
حيث هو تقييد إلى ، هو تمثيل وإدراج هي مخطط مكافئ. حاصل القسمة يمكن أيضاً تحويلها إلى تمثيل . إذا احتوى على تمثيلان فرعيان بالضبط، وهما فضاء جزئي بسيط {0} و نفسها، فيمكن أن يقال عن التمثيل غير قابل للاختزال; إذا احتوت على تمثيل ثانوي مناسب غير بسيط، ويقال أن التمثيل يكون قابل للاختزال.[19] يتضمن تعريف التمثيل غير القابل للاختزال ليما شور: مخطط مكافئ
بين التمثيلات غير القابلة للاختزال إما المخطط الصفري أو تماثل الشكل، نظراً لأن النواة و الصورة هي تمثيلات فرعية. خاصه، عندما، هذا يدل على أن المعادلة تشابه الشكل من الشكل الترابطي لقسمة الجبر على الحقل الأساسي F. إذا كان F مغلق جبرياً، فإن الأشكال المتشابهة الوحيدة للتمثيل غير القابل للاختزال هي المضاعفات العددية للمطابقة. التمثيلات غير القابلة للاختزال هي اللبنات الأساسية لنظرية التمثيل للعديد من المجموعات: إذا كان التمثيل غير قابل للاختزال، فإنه يتم بناؤه من تمثيل ثانوي وحاصل قسمة "أبسط" بمعنى ما؛ على سبيل المثال، إذا كان ذو بُعد محدود، فإن كلا من التمثيل الفرعي والحاصل لهما بُعد أصغر. هناك أمثلة معاكسة حيث يكون للتمثيل تمثيل فرعي، ولكن يحتوي فقط على مكون واحد غير بسيط غير قابل للاختزال. على سبيل المثال، المجموعة المضافة كتمثيل ثنائي الأبعاد
هذه المجموعة لديها المتجه تم إصلاحه من خلال هذا التشابه، ولكن يتم تعيين الفضاء الفرعي التكميلي لـ
إعطاء تمثيل فرعي واحد غير قابل للاختزال. هذا صحيح بالنسبة لجميع المجموعات أحادية القوة[20]pg 112.
المجموعات المباشرة والتمثيلات الغير قابلة للتحليل
إذا كانت (V,φ) و (W,ψ) تمثل (على سبيل المثال) المجموعة G، فإن المجموع المباشر لـ V وW هو تمثيل بطريقة قانونية متعارف بها، عبر المعادلة
لا يحمل المجموع المباشر لتمثيلين مزيداً من المعلومات حول المجموعة G أكثر من التمثيلين الفرديين. إذا كان التمثيل هو المجموع المباشر لاثنين من التمثيلات الفرعية غير البسيطة، فيقال أنه قابل للتحليل. خلاف ذلك، يقال أنه لا يمكن تحليله.
الاختزال الكامل
في الظروف المواتية، يكون كل تمثيل ذي بعد محدود عبارة عن مجموع مباشر من التمثيلات غير القابلة للاختزال: ويقال إن مثل هذه التمثيلات نصف بسيطة. في هذه الحالة ، يكفي أن نفهم فقط التمثيلات غير القابلة للاختزال. تتضمن الأمثلة التي تحدث فيها ظاهرة " اختزال كامل" المجموعات المحدودة والمضغوطة، وجبر لي شبه البسيط.
في الحالات التي لا تكون فيها القابلية للاختزال كاملة، يجب على المرء أن يفهم كيف يمكن بناء التمثيلات غير القابلة للتحلل من تمثيلات غير قابلة للاختزال كتمديدات لحاصل القسمة من خلال تمثيل فرعي.
نواتج موتر التمثيلات
لنفترض و هي تمثيلات لمجموعة . فيمكننا تكوين تمثيل لـ G يعمل على فضاء متجه الناتج الموتر كالتالي:[21]
- .
إذا كان و هي تمثيلات لجبر لي، فإن الصيغة الصحيحة لاستخدامها هي[22]
- .
يمكن التعرف على هذا الناتج على أنه ناتج مشترك على الجبر المشنرك. بشكل عام، ناتج الموتر للتمثيلات غير القابلة للاختزال هو ليس غير قابل للاختزال؛ تُعرف عملية تحليل ناتج موتر كمجموع مباشر للتمثيلات غير القابلة للاختزال باسم نظرية كليبش - جوردان.
في حالة نظرية تمثيل لمجموعة SU(2) (أو ما يعادله من تكيف جبر لي المعقد )، فمن السهل العمل على التحليل.[23] يتم تسمية التمثيلات غير القابلة للاختزال بواسطة الپارامتر وهو عدد صحيح غير سالب أو نصف عدد صحيح؛ ثم التمثيل له . لنفترض أننا أخذنا حاصل الضرب الموتر لتمثيل تمثيلين، مع التسميات و حيث نفترض . ثم يتم تحليل ناتج الموتر كمجموع مباشر لنسخة واحدة من كل تمثيل مع التسمية ، حيث يترواح من إلى بزيادات من 1. إذا، على سبيل المثال، ، ثم قيم التي تحدث على 0، 1 و2. وهكذا، يتحلل تمثيل الناتج الموتر للبعد كمجموع مباشر لتمثيل أحادي البعد تمثيل ثلاثي الأبعاد and وتمثيل خماسي الأبعاد .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التفرعات والموضوعات
تتميز نظرية التمثيل بعدد الفروع التي تمتلكها، وتنوع مناهج دراسة تمثيلات المجموعات والجبر. على الرغم من أن جميع النظريات تشترك في المفاهيم الأساسية التي تمت مناقشتها بالفعل، إلا أنها تختلف اختلافاً كبيراً في التفاصيل. تكون الاختلافات 3 أقسام على الأقل:
- تعتمد نظرية التمثيل على نوع الكائن الجبري الذي يتم تمثيله. هناك عدة فئات مختلفة من المجموعات ، الجبر الترابطي وعلم الجبر، وجميع نظريات تمثيلهم لها صفة مميزة فردية.
- تعتمد نظرية التمثيل على طبيعة الفضاء المتجه الذي يمثل الكائن الجبري عليه. أهم تمييز هو بين تمثيلات ذات أبعاد محدودة والتمثيلات ذات الأبعاد اللانهائية. في حالة الأبعاد اللانهائية، تكون الهياكل الإضافية مهمة (على سبيل المثال، ما إذا كان الفضاء عبارة عن فضاء هيلبرت، فضاء باناخ، وما إلى ذلك). يمكن أيضاً فرض بنى جبرية إضافية في حالة الأبعاد المحدودة.
- تعتمد نظرية التمثيل على نوع المجال الذي يتم من خلاله تحديد فضاء المتجه. أهم الحالات هي مجال الأعداد المركبة، ومجال الأعداد الحقيقية، المجالات المحدودة، ومجالات p-adic numbers. تنشأ صعوبات إضافية لمجالات الخاصية الإيجابية والمجالات غير المغلقة جبرياً.
المجموعات المنتهية
تعتبر تمثيلات المجموعات أداةً مهمة جداً في دراسة المجموعات المنتهية.[24]تظهر أيضًا في تطبيقات نظرية المجموعة المنتهية في الهندسة و علم البلورات.[25] وتُظهر تمثيلات المجموعات المنتهية العديد من سمات النظرية العامة وتشير إلى الفروع والموضوعات الأخرى في نظرية التمثيل.
على مجال الخاصية الصفرية، فإن تمثيل مجموعة منتهية G له عدد من الخصائص الملائمة. أولاً، تمثيلات G شبه بسيطة (قابلة للاختزال تماماً). هذه نتيجة نظرية ماشكي، التي تنص على أن أي تمثيل فرعي V لـ تمثيل-G وW له مكمل G - ثابت. أحد الأدلة هو اختيار أي الإسقاط π من W إلى V واستبداله بمتوسطه πG المعرف ب
πG متكافئة، ونواتها هي التكملة المطلوبة.
يمكن فهم G ذات الأبعاد المحدودة - باستخدام نظرية الميزة: خاصية التمثيل φ: G → GL(V) هي تابع الفئة χφ: G → F المعرف ب
حيث هو الأثر. يتم تحديد التمثيل غير القابل للاختزال لـ G تماماً من خلال خاصيته.
تنطبق نظرية ماشكي بشكل عام على مجالات الخاصية الإيجابية p ، مثل المجال المحدود، طالما أن p الأولية هي coprime إلى ترتيب من G. عندما p و | G | لها عامل مشترك، هناك تمثيلات-G ليست شبه بسيطة، والتي تمت دراستها في فرع ثانوي يسمى نظرية التمثيل المعياري.
تُظهر تقنيات حساب المتوسط أيضاً أنه إذا كانت F هي الأرقام الحقيقية أو المركب ، فإن أي تمثيل-G يحتفظ بالناتج الداخلي على V بمعنى أن
على كل g في G و v, w في W. ومن ثم أي تمثيل-G هو أحادي.
التمثيلات الوحدوية تكون شبه بسيطة تلقائياً، حيث يمكن إثبات نتيجة ماشكي بأخذ التكملة المتعامدة من التمثيل الفرعي. عند دراسة تمثيلات المجموعات غير المحدودة، توفر التمثيلات الوحدوية تعميماً جيداً للتمثيلات الحقيقية والمعقدة لمجموعة منتهية.
يمكن تعميم نتائج مثل نظرية ماشكي والخصوصية الوحدوية التي تعتمد على المتوسط على مجموعات أكثر عمومية عن طريق استبدال المتوسط بكامل، بشرط أن يتم تحديد مفهوم مناسب للتكامل. يمكن القيام بذلك لـ المجموعات الطوبولوجية المدمجة (بما في ذلك مجموعات لي المدمجة)، باستخدام مقياس هار، وتُعرف النظرية الناتجة باسم التحليل التوافقي المجرد.
في المجالات العشوائية، هناك فئة أخرى من المجموعات المحدودة التي لها نظرية تمثيل جيدة هي المجموعات المحدودة من نوع لي. الأمثلة المهمة هي المجموعة الجبرية الخطية على الحقول المحددة. توسع نظرية تمثيل المجموعات الجبرية الخطية و مجموعة لي هذه الأمثلة إلى مجموعات لا نهائية الأبعاد، حيث ترتبط هذه الأخيرة ارتباطاً وثيقاً بـ تمثيل جبر لي. أهمية نظرية الشخصية للمجموعات المحدودة لها نظير في نظرية الأوزان لتمثيل مجموعات لي وجبر لي.
ترتبط تمثيلات مجموعة محدودة G أيضاً بشكل مباشر بتمثيل الجبر عبر مجموعة الجبر F[G]، وهي مساحة متجهية فوق F مع عناصر G كأساس، ومجهزة بعملية الضرب المحددة من قبل عملية المجموعة، الخطية، وشروط عملية المجموعة وانتقال الضرب القياسي.
التمثيلات المعيارية
التمثيلات المعيارية لمجموعة G منتهية هي تمثيلات على مجال لا تعتبر خصائصه coprime لـ | G |، بحيث لم تعد نظرية ماشكي صالحة (لأن | G | ليست قابلة للعكس في F وبالتالي لا يمكن تقسيمها).[26] ومع ذلك، وسع رتشارد براور الكثير من نظرية الميزة إلى التمثيلات المعيارية، ولعبت هذه النظرية دورًا مهمًا في التقدم المبكر نحو تصنيف المجموعات البسيطة المنتهية ، خاصة بالنسبة للمجموعات البسيطة التي لم يكن توصيفها قابلاً للتطبيق تمامًا الطرق النظرية للمجموعة لأن مجموعة Sylow 2 الفرعية كانت "صغيرة جداً".[27]
بالإضافة إلى وجود تطبيقات لنظرية المجموعة، تنشأ التمثيلات المعيارية بشكل طبيعي في فروع أخرى من الرياضيات، مثل الهندسة الجبرية و نظرية التشفير و التوافقية و نظرية الأعداد.
التمثيل الوحدوي
التمثيل الوحدوي للمجموعة G هو تمثيل خطي φ لـ G على فضاء هلبرت حقيقي أو (عادةً) مركب V مثلφ(g) وهو العامل الموحد لكل g ∈ G. تم تطبيق مثل هذه التمثيلات على نطاق واسع في ميكانيكا الكم منذ عشرينيات القرن الماضي، وذلك بفضل تأثير هيرمان ويل،[28] وقد ألهم هذا تطوير النظرية، وعلى الأخص من خلال تحليل تمثيلات مجموعة پوانكاريه بواسطة يوجين وينر.[29]كان جورج ماكي أحد الرواد في بناء نظرية عامة للتمثيلات الأحادية (لأي مجموعة G وليس لمجموعات معينة مفيدة في التطبيقات فقط)، وقد طور هارش-تشاندرا وآخرون في الخمسينيات والستينيات من القرن الماضي ملحق هذه النظرية.[30]
الهدف الرئيسي هو وصف "ثنائية وحدوية"، فضاء التمثيلات الأحادية غير القابلة للاختزال لـ G.[31]تكون النظرية أكثر تطوراً في حالة أن G عبارة عن مجموعة طوبولوجية مدمجة محلياً (هسدورف) والتمثيلات مستمرة بفعالية.[11] بالنسبة لأبيليان G، فإن الثنائية الوحدوية هي مجرد فضاء الخصائص، بينما بالنسبة لـ G المدمجة، تُظهر نظرية پيتر-ويل أن التمثيلات الأحادية غير القابلة للاختزال الأبعاد المحدودة والثنائية الوحدوية منفصلة.[32] على سبيل المثال، إذا كانت G هي مجموعة الدوائر S1، فسيتم إعطاء الخصائص بواسطة أعداد صحيحة، ويكون الثنائي الأحادي هو Z.
بالنسبة إلى G غير المدمجة، فإن السؤال عن أي التمثيلات وحدوية هو سؤال دقيق. على الرغم من أن التمثيلات الوحدوية غير القابلة للاختزال يجب أن تكون "مقبولة" (مثل وحدة هارش-شاندرا ومن السهل اكتشاف التمثيلات المقبولة التي لها شكل خطي متماثل ثوابت غير مُنشئة، فمن الصعب تحديد متى يكون هذا النموذج إيجابياً محدداً. لا يزال الوصف الفعال للازدواج الوحدوي، حتى بالنسبة للمجموعات الفعالة نسبياً مثل مجموعة لي الاختزالية (تمت مناقشتها أدناه)، وهي مسألة مفتوحة مهمة في نظرية التمثيل. تم حلها للعديد من المجموعات المحددة، مثل SL(2,R) و مجموعة لورنتز .[33]
التحليل التوافقي
الازدواجية بين مجموعة الدوائر S1 والمحارف Z، أو بشكل أعم بين مستديرة Tn و Zn تُعرف في التحليل بنظرية سلسلة فورييه، ويعبر تحويل فورييه بالمثل عن حقيقة أن فضاء الأحرف على فضاء متجه حقيقي هي فضاء متجه مزدوج. وبالتالي، ترتبط نظرية التمثيل الوحدوي و التحليل التوافقي ارتباطاً وثيقاً، ويستغل التحليل التوافقي المجرد هذه العلاقة، من خلال تطوير التحليل للتوابع على المجموعات الطوبولوجية المدمجة محلياً وما يتصل بها من فضاءات.[11]
الهدف الرئيسي هو توفير شكل عام لتحويل فورييه و نظرية پلانشريل. يتم ذلك عن طريق بناء قياس على ثنائي وحدوي وتماثل بين التمثيل المنتظم لـ G على الفضاء L2(G)( توابع G ) لـ تكامل مربع على G وتمثيلها في توابع فضاء L2 على الثنائي الوحدوي. ازدواجية پونترجاين و نظرية پيتر-ويل تحقق ذلك من أجل G الأبليانية والمدمجة.[32][34]
نهج آخر ينطوي على النظر في جميع التمثيلات الوحدوية، وليس فقط غير القابلة للاختزال. وتشكل تلك التصنيف، و ثنائية تاناكا-كرين التي توفر طريقة لاستعادة مجموعة مدمجة من فئة التمثيلات الأحادية الخاصة بها.
إذا لم تكن المجموعة أبيلية أو مدمجة، فلا توجد نظرية عامة معروفة بوجود نظير لنظرية پلانشيريل أو انعكاس فورييه، على الرغم من أن ألكسندر گروتينديك قام بتوسيع ثنائية تاناكا-كيرين إلى علاقة بين مجموعة جبرية خطية و تصنيفات تاناكيان.
تم أيضاً توسيع التحليل التوافقي من تحليل التوابع في مجموعة G إلى توابع على فضاءات متجانسة لـG. تم تطوير النظرية بشكل جيد من أجل الفضاء المتماثل وتوفر نظرية الصيغ الآلية (نوقشت أدناه).
مجموعات لي
| Group theory → زُمـَر لي زُمـَر لي |
|---|
 |
مجموعة لي هي مجموعة هي أيضاً متضاعفة سلسة. العديد من مجموعات المصفوفات الكلاسيكية على الأعداد الحقيقية أو المركبة هي مجموعات لي.[35] العديد من المجموعات المهمة في الفيزياء والكيمياء هي مجموعات لي، ونظرية التمثيل الخاصة بهم ضرورية لتطبيق نظرية المجموعة في تلك المجالات.[9]
يمكن تطوير نظرية التمثيل لمجموعات لي أولاً من خلال النظر في المجموعات المدمجة، والتي تنطبق عليها نتائج نظرية التمثيل المدمج.[31] يمكن توسيع هذه النظرية لتشمل تمثيلات ذات أبعاد محدودة ل مجموعة لي شبه بسيطة باستخدام خدعة ويل الوحدوية: كل مجموعة لي شبه بسيطة حقيقية G لها تعقيد، وهو مجموعة لي معقدة Gc، ومجموعة لي المعقدة هذه تحتوي على أقصى مجموعة فرعية مدمجة K. تتوافق التمثيلات ذات الأبعاد المحدودة لـG بشكل وثيق مع تمثيلات K.
مجموعة لي العامة هي ناتج شبه مباشر من مجموعة لي القابلة للحل ومجموعة لي شبه بسيطة (تحليل ليڤي).[36] يعتبر تصنيف تمثيلات مجموعات لي القابلة للحل أمراً صعباً بشكل عام، ولكنه غالباً ما يكون سهلاً في الحالات العملية. يمكن بعد ذلك تحليل تمثيلات المنتجات شبه المباشرة عن طريق النتائج العامة المسماة نظرية ماكي، وهي تعميم للطرق المستخدمة في تصنيف وگنر لتمثيلات مجموعة پوانكاريه.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
جبر لي
جبر لي على المجال F هو فضاء متجه على F مزود بـ انحراف متماثل عملية ثنائية الخطية تسمى قوس لي، والتي تحقق مطابقة جاكوبي. يظهر جبر لي على وجه الخصوص على أنه فضاء مماسي لـ مجموعة لي في عنصر المطابقة، مما يؤدي إلى تفسيرها على أنها "تماثلات متناهية الصغر".[36]تتمثل إحدى الطرق المهمة لنظرية تمثيل مجموعات لي في دراسة نظرية التمثيل المقابلة لجبر لي، ولكن تمثيلات الجبر لي أيضاً لها اهتمام جوهري.[37]
يحتوي جبر لي، مثل مجموعات لي، على تحليل ليڤي إلى أجزاء شبه بسيطة وقابلة للحل، مع نظرية تمثيل جبر لي القابلة للحل بشكل عام. في المقابل، فإن تمثيلات الأبعاد المحدودة لجبر لي شبه البسيط مفهومة تماماً، بعد عمل إيلي كارتان. يتم تحليل تمثيل جبر لي شبه بسيط 𝖌 عن طريق اختيار جبر كارتان الفرعي، والذي يعد أساساً جبرياً فرعياً أعظمياً عاماً 𝖍 لـ حيث يكون قوس لي صفراً ("أبيليان"). يمكن أن يتحلل تمثيل إلى فضاءات الوزن وهي عبارة عن فضاء مميز لسلوك 𝖍 والتناظرية متناهية الصغر من الخصائص. ثم يقلل هيكل جبر لي شبه البسيط من تحليل التمثيلات إلى توليفات سهلة الفهم للأوزان المحتملة التي يمكن أن تحدث.[36]
جبر لي ذو الأبعاد اللانهائية
هناك العديد من فئات الجبر اللامتناهي الأبعاد التي تمت دراسة تمثيلاتها. من بين هؤلاء، فئة مهمة وهي Kac – Moody algebras.[38] تم تسميتهم على اسم ڤيكتور كاك و روبرت مودي، اللذين قامو باكتشافها بشكل مستقل. يشكل هذه الجبر تعميماً للأبعاد المحدودة جبر لي شبه بسيط، وتشترك في العديد من خصائصها التوافقية. هذا يعني أن لديهم فئة من التمثيلات التي يمكن فهمها بنفس طريقة تمثيلات جبر لي شبه البسيطة.
تعد جبر أفين لي حالة خاصة من جبر كاك-مودي، والتي لها أهمية خاصة في الرياضيات و الفيزياء النظرية، وخاصة نظرية المجال المطابق ونظرية النموذج المضبوط القابل للحل. اكتشف كاك برهاناً على مطابقات اندماجية معينة، مطابقات ماكدونالد، والتي تستند إلى نظرية التمثيل لجبر أفين كاك-مودي.
جبر لي الفائق
جبر لي الفائق عبارة عن تعميمات لجبر لي حيث يحتوي الفضاء المتجه الأساسي على Z2-التحريف والتماثل والانحراف وخصائص مطابقة جاكوبي لقوس لي التي يتم تعديلها بواسطة الإشارات. وتتشابه نظرية التمثيل الخاصة بهم نظرية التمثيل لجبر لي.[39]
المجموعات الجبرية الخطية
المجموعات الجبرية الخطية (أو بشكل عام، مخططات المجموعة الأفينية) هي نظائرها في الهندسة الجبرية لـ مجموعة لي، ولكن على المجالات العامة أكثر من مجرد R أو C. على وجه الخصوص، في المجالات المحدودة، فإنها تؤدي إلى مجموعات محدودة من نوع لي. على الرغم من أن المجموعات الجبرية الخطية لها تصنيف مشابه جداً لتصنيف مجموعات لي، إلا أن نظرية التمثيل الخاصة بهم مختلفة نوعاً ما (ومفهومة جيداً بشكل أقل) وتتطلب تقنيات مختلفة، نظراً لأن طوبولوجيا زاريسكي ضعيفة نسبياً، وتقنيات من التحليل التي لم تعد متاحةً.[40]
نظرية الثوابت
دراسات نظرية الثوابث إجراءات على أصناف جبرية من وجهة نظر تأثيرها على الدوال التي تشكل تمثيلات المجموعة. تقليدياً، تناولت النظرية مسألة الوصف الواضح لـ تابع متعدد الحدود اللامتغير، أو الثابت، في ظل التحولات من مجموعة خطية معينة. يحلل النهج الحديث تحليل هذه التمثيلات إلى غير قابلة للاختزال.[41]
ترتبط نظرية الثوابت لـ مجموعة لانهائية ارتباطاً وثيقاً بتطور الجبر الخطي، وخاصة نظريات الشكل التربيعي و المحددات. موضوع آخر له تأثير متبادل قوي هو الهندسة الإسقاطية، حيث يمكن استخدام النظرية الثابتة لتنظيم الموضوع، وخلال الستينيات، تم إحياء في الموضوع بواسطة ديڤد مومفورد في صيغة ديڤد مومفورد نظرية الثوابت الهندسية.[42]
تعود جذور نظرية تمثيل مجموعة لي شبه بسيطة إلى النظرية الثابتة[35] والروابط القوية بين نظرية التمثيل والهندسة الجبرية التي لها العديد من أوجه التشابه في الهندسة التفاضلية، بدءاً من برنامج إرلانگن فيلكس كلاين و علاقات إيلي كارتان، والتي تضع المجموعات والتناظر في قلب الهندسة.[43] تربط التطورات الحديثة نظرية التمثيل والنظرية الثابتة بمجالات متنوعة مثل الشمولية، العامل التفاضلي ونظرية المتغيرات المعقدة المتعددة.
الأشكال الآلية ونظرية الأعداد
الأشكال التلقائية هي تعميم لـ النماذج المعيارية إلى دوال تحليلية أكثر عمومية، ربما لـ متغيرات معقدة متعددة، مع خصائص تحويل مماثلة.[44] يتضمن التعميم استبدال المجموعة المعيارية PSL2 (R) ومجموعة مختارة كالمجموعة المتوافقة الفرعية بمجموعة لي شبه بسيطة G و المجموعة المتقطعة الفرعية Γ. تماماً كما يمكن عرض النماذج المعيارية على أنها شكل تفاضلي على حاصل فضاء النصف العلوي H = PSL2 (R)/SO(2)، يمكن النظر إلى الأشكال ذات الشكل التلقائي كأشكال تفاضلية (أو كائنات مماثلة) في Γ\G/K هو (عادةً) مجموعة دمج أقصى فرعية من G. ومع ذلك، هناك حاجة إلى بعض الانتباه، حيث أن الحاصل عادةً ما يحتوي على فرادات. حاصل مجموعة لي شبه بسيطة من قبل مجموعة فرعية مدمجة هو فضاء متماثل وبالتالي فإن نظرية الأشكال التلقائية ترتبط ارتباطاً وثيقاً بالتحليل التوافقي على الفضاءات المتماثلة.
قبل تطوير النظرية العامة، تمت صياغة العديد من الحالات الخاصة المهمة بالتفصيل، بما في ذلك صيغة هلبرت المعيارية و صيغة سيگل المعيارية. تتضمن النتائج المهمة في النظرية صيغة تتبع سيلبرگ وتحقيق روبرت لانگلاندز أنه يمكن تطبيق نظرية ريمان-روخ لحساب أبعاد فضاء الأشكال ذات الشكل الآلي. أثبت المفهوم اللاحق لـ "التمثيل الآلي" قيمة تقنية كبيرة للتعامل مع الحالة التي تكون فيها G مجموعة جبرية، يتم التعامل معها على أنها مجموعة أديليك جبرية. نتيجة لذلك، تم تطوير فلسفة كاملة، برنامج لانگلاند حول العلاقة بين التمثيل والخصائص النظرية للأرقام للأشكال ذات الشكل الآلي.[45]
الجبر الترابطي
بمعنى ما، فإن تمثيلات الجبر الترابطي تعمم تمثيلات المجموعات وجبر لي. يؤدي تمثيل المجموعة إلى تمثيل حلقة المجموعة أو جبر المجموعة، بينما تتوافق تمثيلات جبر لي بشكل حيوي مع تمثيلات الجبر المغلف الشامل. ومع ذلك، فإن نظرية التمثيل للجبر الترابطي العام لا تحتوي على جميع الخصائص الجيدة لنظرية تمثيل المجموعات وجبر لي.
النظرية المعيارية
عند النظر في تمثيلات الجبر الترابطي، يمكن للباحث أن ينسى المجال الأساسي، وأن ينظر ببساطة إلى الجبر الترابطي باعتباره حلقة، وتمثيلاته كوحدات نمطية. هذا النهج مثمر بشكل مدهش: يمكن تفسير العديد من النتائج في نظرية التمثيل على أنها حالات خاصة من النتائج حول وحدات على حلقة.
جبر هوپف ومجموعات الكم
يوفر جبر هوپف طريقة لتحسين نظرية التمثيل للجبر الترابطي، مع الإبقاء على نظرية التمثيل للمجموعات و جبر لي كحالات خاصة. على وجه الخصوص، ناتج الموتر لتمثيلين هو تمثيل، وكذلك فضاء المتجه المزدوج.
يمتلك جبر هوپف المرتبط بالمجموعات بنية جبرية تبادلية، ولذا يُعرف جبر هوپف العام باسم المجموعة الكمومية، على الرغم من أن هذا المصطلح غالباً ما يقتصر على بعض جبر هوپف الذي ينشأ على شكل تشوهات للمجموعات أو جبرها المغلف الشامل. أضافت نظرية تمثيل المجموعات الكمومية رؤى مدهشة إلى نظرية تمثيل مجموعات لي وجبر لي، على سبيل المثال من خلال الأساس البلوري لكاشيوارا.
التعميمات
تمثيلات المجموعة النظرية
يُعرف تمثيل مجموعة نظرية (أيضًا باسم أثر مجموعة أو تمثيل تبديل) لـ مجموعة G على مجموعة X تُعطى بواسطة دالة 'ρ من G إلى XX، مجموعة من دوال من X إلى X، مثل لجميع g1، g2 في G وجميع x في X:
يشير هذا الشرط والبديهيات لمجموعة ما إلى أن ρ(g) هي انحياز (أو تبديل) لكل g في G. وبالتالي قد نحدد تمثيل التبديل على نحو مكافئ ليكون مجموعة تماثل الشكل من G إلى مجموعة متماثلة SX لـ X.
التمثيلات في تصنيفات أخرى
يمكن النظر إلى كل مجموعة G على أنها تصنيف مع كائن واحد؛ التشكل في هذا التصنيف ليس سوى عناصر G. بالنظر إلى فئة عشوائية C، فإن تمثيل لـ G في C هو عامل من G إلى G. يختار هذا العامل كائنًا X في C ومجموعة تشابه جماعي من G إلى Aut(X)، مجموعة تشكل ذاتي لـ X.
في الحالة التي يكون فيها C VectF، تصنيف فضاءات المتجه على مجال F، هذا التعريف يعادل التمثيل الخطي. وبالمثل، فإن التمثيل النظري للمجموعة هو مجرد تمثيل G في تصنيف المجموعات.
للحصول على مثال آخر، لنضع في الاعتبار تصنيف الفضاءات الطوبولوجية، أعلى. التمثيلات في الأعلى هي تشابهات من G إلى مجموعة تشكل ذاتي للفضاء الطوبولوجي X.
لدينا نوعان من التمثيلات وثيقة الصلة بالتمثيلات الخطية هما:
- التمثيل الإسقاطي: في تصنيف الفضاء الإسقاطي. يمكن وصفها بأنها "تمثيلات خطية تصل إلى تحويلات سُلَّمية".
- تمثيل أفيني: في تصنيف فضاء أفيني. على سبيل المثال، تعمل المجموعة الإقليدية بشكل وثيق على الفضاء الإقليدي.
تمثيلات التصنيفات
نظرًا لأن المجموعات هي تصنيفات، يمكن للمرء أيضاً التفكير في تمثيل التصنيفات الأخرى. أبسط تعميم هو الأحادية، وهي فئات ذات كائن واحد. المجموعات هي أحاديات يكون كل شكل فيها قابلاً للعكس. أحاديات عامة لها تمثيلات في أي تصنيف. في تصنيف المجموعات، وهي عمل أحادي، ولكن يمكن دراسة التمثيلات أحادية الصيغة على فضاءات متجهة وكائنات أخرى.
بشكل عام، يمكن للباحث أن يخفف من الافتراض القائل بأن التصنيف الذي يتم تمثيله له كائن واحد فقط. بشكل أعم، هذه مجرد نظرية العاملات بين التصنيفات، ويمكن قول القليل.
كان لحالة خاصة واحدة تأثير كبير على نظرية التمثيل، وهي نظرية تمثيل كويڤر.[15] كويڤر هي ببساطة الرسم البياني الموجه (مع السماح بالحلقات والأسهم المتعددة)، ولكن يمكن تحويلها إلى تصنيف (وكذلك الجبر) من خلال النظر في المسارات في الرسم البياني. لقد أضاءت تمثيلات مثل هذه التصنيفات / الجبر العديد من جوانب نظرية التمثيل، على سبيل المثال من خلال السماح لأسئلة نظرية التمثيل والتي ليست شبه البسيطة حول مجموعة ليتم اختزالها في بعض الحالات إلى أسئلة نظرية التمثيل شبه البسيطة حول كويڤر.
انظر أيضاً
ملاحظات
- ^ "The Definitive Glossary of Higher Mathematical Jargon — Mathematical Representation". Math Vault (in الإنجليزية الأمريكية). 2019-08-01. Retrieved 2019-12-09.
- ^ Classic texts on representation theory include Curtis & Reiner (1962) and Serre (1977). Other excellent sources are Fulton & Harris (1991) and Goodman & Wallach (1998).
- ^ "representation theory in nLab". ncatlab.org. Retrieved 2019-12-09.
- ^ For the history of the representation theory of finite groups, see Lam (1998). For algebraic and Lie groups, see Borel (2001).
- ^ أ ب ت Etingof, Pavel; Golberg, Oleg; Hensel, Sebastian; Liu, Tiankai; Schwendner, Alex; Vaintrob, Dmitry; Yudovina, Elena (January 10, 2011). "Introduction to representation theory" (PDF). www-math.mit.edu. Retrieved 2019-12-09.
- ^ أ ب There are many textbooks on vector spaces and linear algebra. For an advanced treatment, see Kostrikin & Manin (1997).
- ^ Sally & Vogan 1989.
- ^ أ ب ت Teleman, Constantin (2005). "Representation Theory" (PDF). math.berkeley.edu. Retrieved 2019-12-09.
- ^ أ ب Sternberg 1994.
- ^ Lam 1998, p. 372.
- ^ أ ب ت Folland 1995.
- ^ Goodman & Wallach 1998, Olver 1999, Sharpe 1997.
- ^ Borel & Casselman 1979, Gelbart 1984.
- ^ See the previous footnotes and also Borel (2001).
- ^ أ ب Simson, Skowronski & Assem 2007.
- ^ Fulton & Harris 1991, Simson, Skowronski & Assem 2007, Humphreys 1972.
- ^ This material can be found in standard textbooks, such as Curtis & Reiner (1962), Fulton & Harris (1991), Goodman & Wallach (1998), Gordon & Liebeck (1993), Humphreys (1972), Jantzen (2003), Knapp (2001) and Serre (1977).
- ^ أ ب Serre 1977.
- ^ The representation {0} of dimension zero is considered to be neither reducible nor irreducible, just like the number 1 is considered to be neither composite nor prime.
- ^ Humphreys, James E. (1975). Linear Algebraic Groups. New York, NY: Springer New York. ISBN 978-1-4684-9443-3. OCLC 853255426.
- ^ Hall 2015 Section 4.3.2
- ^ Hall 2015 Proposition 4.18 and Definition 4.19
- ^ Hall 2015 Appendix C
- ^ Alperin 1986, Lam 1998, Serre 1977.
- ^ Kim 1999.
- ^ Serre 1977, Part III.
- ^ Alperin 1986.
- ^ See Weyl 1928.
- ^ Wigner 1939.
- ^ Borel 2001.
- ^ أ ب Knapp 2001.
- ^ أ ب Peter & Weyl 1927.
- ^ Bargmann 1947.
- ^ Pontrjagin 1934.
- ^ أ ب Weyl 1946.
- ^ أ ب ت Fulton & Harris 1991.
- ^ Humphreys 1972a.
- ^ Kac 1990.
- ^ Kac 1977.
- ^ Humphreys 1972b, Jantzen 2003.
- ^ Olver 1999.
- ^ Mumford, Fogarty & Kirwan 1994.
- ^ Sharpe 1997.
- ^ Borel & Casselman 1979.
- ^ Gelbart 1984.
المراجع
- Alperin, J. L. (1986), Local Representation Theory: Modular Representations as an Introduction to the Local Representation Theory of Finite Groups, Cambridge University Press, ISBN 978-0-521-44926-7.
- Bargmann, V. (1947), "Irreducible unitary representations of the Lorenz group", Annals of Mathematics 48 (3): 568–640, doi:.
- Borel, Armand (2001), Essays in the History of Lie Groups and Algebraic Groups, American Mathematical Society, ISBN 978-0-8218-0288-5.
- Borel, Armand; Casselman, W. (1979), Automorphic Forms, Representations, and L-functions, American Mathematical Society, ISBN 978-0-8218-1435-2.
- Curtis, Charles W.; Reiner, Irving (1962), Representation Theory of Finite Groups and Associative Algebras, John Wiley & Sons (Reedition 2006 by AMS Bookstore), ISBN 978-0-470-18975-7, https://archive.org/details/representationth11curt.
- Gelbart, Stephen (1984), "An Elementary Introduction to the Langlands Program", Bulletin of the American Mathematical Society 10 (2): 177–219, doi:.
- Folland, Gerald B. (1995), A Course in Abstract Harmonic Analysis, CRC Press, ISBN 978-0-8493-8490-5.
- قالب:Fulton-Harris.
- Goodman, Roe; Wallach, Nolan R. (1998), Representations and Invariants of the Classical Groups, Cambridge University Press, ISBN 978-0-521-66348-9.
- James, Gordon; Liebeck, Martin (1993), Representations and Characters of Finite Groups, Cambridge: Cambridge University Press, ISBN 978-0-521-44590-0.
- Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, 222 (2nd ed.), Springer, ISBN 978-3319134666
- Helgason, Sigurdur (1978), Differential Geometry, Lie groups and Symmetric Spaces, Academic Press, ISBN 978-0-12-338460-7
- Humphreys, James E. (1972a), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7, https://archive.org/details/introductiontoli00jame.
- Humphreys, James E. (1972b), Linear Algebraic Groups, Graduate Texts in Mathematics, 21, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90108-4
- Jantzen, Jens Carsten (2003), Representations of Algebraic Groups, American Mathematical Society, ISBN 978-0-8218-3527-2.
- Kac, Victor G. (1977), "Lie superalgebras", Advances in Mathematics 26 (1): 8–96, doi:.
- Kac, Victor G. (1990), Infinite Dimensional Lie Algebras (3rd ed.), Cambridge University Press, ISBN 978-0-521-46693-6.
- Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4.
- Kim, Shoon Kyung (1999), Group Theoretical Methods and Applications to Molecules and Crystals: And Applications to Molecules and Crystals, Cambridge University Press, ISBN 978-0-521-64062-6.
- Kostrikin, A. I.; Manin, Yuri I. (1997), Linear Algebra and Geometry, Taylor & Francis, ISBN 978-90-5699-049-7.
- Lam, T. Y. (1998), "Representations of finite groups: a hundred years", Notices of the AMS 45 (3,4): 361–372 (Part I), 465–474 (Part II).
- Yurii I. Lyubich. Introduction to the Theory of Banach Representations of Groups. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988.
- Mumford, David; Fogarty, J.; Kirwan, F. (1994), Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], 34 (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56963-3; قالب:MathSciNet (2nd ed.); قالب:MathSciNet(3rd ed.)
- Olver, Peter J. (1999), Classical invariant theory, Cambridge: Cambridge University Press, ISBN 978-0-521-55821-1.
- Peter, F.; Weyl, Hermann (1927), "Die Vollständigkeit der primitiven Darstellungen einer geschlossenen kontinuierlichen Gruppe", Mathematische Annalen 97 (1): 737–755, doi:, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0097&DMDID=DMDLOG_0039&L=1.
- Pontrjagin, Lev S. (1934), "The theory of topological commutative groups", Annals of Mathematics 35 (2): 361–388, doi:.
- Sally, Paul; Vogan, David A. (1989), Representation Theory and Harmonic Analysis on Semisimple Lie Groups, American Mathematical Society, ISBN 978-0-8218-1526-7.
- Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, Springer-Verlag, ISBN 978-0387901909, https://archive.org/details/linearrepresenta1977serr.
- Sharpe, Richard W. (1997), Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer, ISBN 978-0-387-94732-7.
- Simson, Daniel; Skowronski, Andrzej; Assem, Ibrahim (2007), Elements of the Representation Theory of Associative Algebras, Cambridge University Press, ISBN 978-0-521-88218-7.
- Sternberg, Shlomo (1994), Group Theory and Physics, Cambridge University Press, ISBN 978-0-521-55885-3, https://archive.org/details/grouptheoryphysi0000ster.
- Tung, Wu-Ki (1985). Group Theory in Physics (1st ed.). New Jersey·London·Singapore·Hong Kong: World Scientific. ISBN 978-9971966577.
- Weyl, Hermann (1928), Gruppentheorie und Quantenmechanik (The Theory of Groups and Quantum Mechanics, translated H.P. Robertson, 1931 ed.), S. Hirzel, Leipzig (reprinted 1950, Dover), ISBN 978-0-486-60269-1.
- Weyl, Hermann (1946), The Classical Groups: Their Invariants and Representations (2nd ed.), Princeton University Press (reprinted 1997), ISBN 978-0-691-05756-9.
- Wigner, Eugene P. (1939), "On unitary representations of the inhomogeneous Lorentz group", Annals of Mathematics 40 (1): 149–204, doi:.
وصلات خارجية
| Find more about فضاء التمثيل at Wikipedia's sister projects | |
| Quotations from Wikiquote | |
- Hazewinkel, Michiel, ed. (2001), "Representation theory", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Alexander Kirillov Jr., An introduction to Lie groups and Lie algebras (2008). Textbook, preliminary version pdf downloadable from author's home page.
- Kevin Hartnett, (2020), article on representation theory in Quanta magazine





![{\displaystyle (2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v}](https://www.marefa.org/api/rest_v1/media/math/render/svg/f161cc2d8891fa83e92614158722dd4713c0bdba)

















































![{\displaystyle \rho (1)[x]=x}](https://www.marefa.org/api/rest_v1/media/math/render/svg/120857e96706f618d4b481e02c9ace79e8a12a0f)
![{\displaystyle \rho (g_{1}g_{2})[x]=\rho (g_{1})[\rho (g_{2})[x]].}](https://www.marefa.org/api/rest_v1/media/math/render/svg/debb023e3f5e4ff703726b78494d7cc8acad5391)