فضاء هلبرت

Hilbert spaces can be used to study the harmonics of vibrating strings.

فضاء هيلبرت هو فضاء معياري معرف عليه دالة الضرب الداخلي بشرط أن يكون المعيار المعرف عليه هو بدلالة دالة الضرب الداخلي هذه, بالإضافة إلى وجوب كونه فضاء معياري كامل أو ما يدعى ب فضاء باناخ. وهذا يعني أن أي فضاء هيلبرت هو فضاء باناخ ولكن العكس غير صحيح.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مقدمة وتاريخ

David Hilbert, the mathematician whose groundbreaking work on the study of integral equations and quadratic forms led to the introduction of the Hilbert space.

 التطبيقات

The orbitals of an electron in a hydrogen atom are eigenfunctions of the energy. The energy is given by the (time-independent) Schrödinger operator acting on a dense subspace of the Hilbert space of square-integrable functions on R³, and its spectrum determines the possible energy levels.

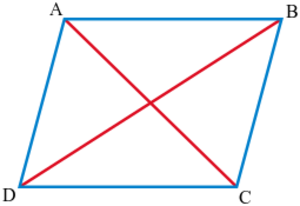
 Parallelogram identity and polarization

Geometrically, the parallelogram identity asserts that AC² + BD² = 2(AB² + AD²). In words, the sum of the squares of the diagonals is twice the sum of the squares of any two adjacent sides.

 طالع ايضاً

• Harmonic analysis
• Hermitian operators
• Hilbert C*-module
• Hilbert manifold
• Mathematical analysis
• Operator algebra
• Rigged Hilbert space
• Reproducing kernel Hilbert space
• Topologies on the set of operators on a Hilbert space

 المصادر

• Bers, Lipman; John, Fritz; Schechter, Martin (1981), Partial differential equations, American Mathematical Society, ISBN 0821800493 .
• Bourbaki, Nicolas (1986), Spectral theories, Elements of mathematics, Berlin: Springer-Verlag, ISBN 0201007673 
• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin: Springer-Verlag, ISBN 978-3540136279 
• Brenner, S.; Scott, R. L. (2005), The Mathematical Theory of Finite Element Methods (2nd ed.), Springer, ISBN 0-3879-5451-1 .
• Clarkson, J. A. (1936), "Uniformly convex spaces", Trans. Amer. Math. Soc. 40: 396–414, http://www.jstor.org/stable/1989630 .
• Courant, Richard; Hilbert, David (1953), Methods of Mathematical Physics, Vol. I, Interscience 
• Dieudonné, Jean (1960), Foundations of Modern Analysis, Academic Press .
• Dunford, N.; Schwartz, J.T. (1958), Linear operators, Parts I and II, Wiley-Interscience .
• Duren, P. (1970), Theory of $H^{p}$-Spaces, New York: Academic Press .
• Folland, Gerald B. (1989), Harmonic analysis in phase space, Annals of Mathematics Studies, 122, Princeton University Press, ISBN 0-691-08527-7 
• Fréchet, Maurice (1907), "Sur les ensembles de fonctions et les opérations linéares", C. R. Acad. Sci. Paris 144: 1414-1416 .
• Fréchet, Maurice (1904-1907), Sur les opérations linéares .
• Giusti, Enrico (2003), Direct Methods in the Calculus of Variations, World Scientific, ISBN 981-238-043-4 .
• Halmos, Paul (1957), Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea Pub. Co 
• Halmos, Paul (1982), A Hilbert Space Problem Book, Springer-Verlag, ISBN

0387906851 

• Hewitt, Edwin; Stromberg, Karl (1965), Real and Abstract Analysis, Springer-Verlag .
• Hilbert, David; Nordheim, Lothar (Wolfgang); von Neumann, John (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen 98: 1-30, http://dz-srv1.sub.uni-goettingen.de/sub/digbib/loader?ht=VIEW&did=D27779 .
• Kolmogorov, Andrey; Fomin, Sergei V. (1970), Introductory Real Analysis (Revised English edition, trans. by Richard A. Silverman (1975) ed.), Dover Press, ISBN 0-486-61226-0 .
• B.M. Levitan (2001), "Hilbert space", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 .
• Reed, Michael; Simon, Barry (1980), Functional Analysis, Methods of Modern Mathematical Physics, Academic Press, ISBN 0-12-585050-6 .
• Reed, Michael; Simon, Barry (1975), Fourier Analysis, Self-Adjointness, Methods of Modern Mathematical Physics, Academic Press, ISBN 0-12-5850002-6 .
• Prugovečki, Eduard (1981), Quantum mechanics in Hilbert space (2nd ed.), Dover (published 2006), ISBN 978-0486453279 .
• Riesz, Frigyes (1907), "Sur une espèce de géométrie analytiques des systèmes de fonctions sommables", C. R. Acad. Sci. Paris 144: 1409-1411 .
• Riesz, Frigyes (1934), "Zur Theories des Hibertschen Raumes", Acta Sci. Math. Szeged 7: 34-38 .
• Riesz, Frigyes; Sz.-Nagy, Béla (1990), Functional analysis, Dover, ISBN 0-486-66289-6 .
• Rudin, Walter (1973), Functional analysis, Tata MacGraw-Hill .
• Schmidt, Erhard (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Rend. Circ. Mat. Palermo 25: 63-77 .
• Saks, Stanisław (2005), Theory of the integral (2nd Dover ed.), Dover, ISBN 978-0486446486 ; originally published Monografje Matematyczne, vol. 7, Warszawa, 1937.
• Stewart, James (2006), Calculus: Concepts and Contexts (3rd ed.), Thomson/Brooks/Cole .
• Titchmarsh, Edward Charles (1946), Eigenfunction expansions, part 1, Oxford University: Clarendon Press .
• von Neumann, John (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen 102: 49-131 .
• von Neumann, John (1932), "Physical Applications of the Ergodic Hypothesis", Proc Natl Acad Sci U S A 18: 263-266, http://www.jstor.org/stable/86260 .
• Walters, Peter (1982), An Introduction to Ergodic Theory, Springer-Verlag, ISBN 0-387-95152-0 .
• Weyl, Hermann (1931), The Theory of Groups and Quantum Mechanics (English 1950 ed.), Dover Press, ISBN 0-486-60269-9 .
• Young, N (1988), An introduction to Hilbert space, Cambridge University Press, ISBN 0-521-33071-8 .
• Zimmer, Robert (1990), Essential Results of Functional Analysis, ISBN 0226983382