مضلع منتظم

فئة المضلعات n-gons المنتظمة المحدبة
المضلعات المنتظمة
الحواف و الرؤوس	n
رمز شلفلي	{n}
مخطط كوكستر-دينكن
مجموعة التماثل	D_n, order 2n
مضلع ثنائي	ذاتي-مزدوج
المساحة (بطول الجانب،, s)	$A={\tfrac {1}{4}}ns^{2}\cot \left({\frac {\pi }{n}}\right)$
الزاوية الداخلية	$(n-2)\times {\frac {180^{\circ }}{n}}$
مجموعة الزوايا الداخلية	$\left(n-2\right)\times 180^{\circ }$
قطر الدائرة المحيطة	$d_{\text{IC}}=s\cot \left({\frac {\pi }{n}}\right)$
قطر الدائرة المحصورة	$d_{\text{OC}}=s\csc \left({\frac {\pi }{n}}\right)$
الخصائص	محدب, دوري, متساوي الاضلاع, متماثل, متساوي

في الهندسة الإقليدية، المضلع المنتظم regular polygon هو كل مضلع بسيط جميع أضلاعه متساوية في الطول وجميع زواياه متساوية في القياس. من الممكن أن يكون المضلع المنتظم محدب أو نجمي. في النهاية، تقترب متسلسلة من المضلعات المنتظمة مع عدد متزايد من الأضلاع من الدائرة، إذا كان المحيط أو المساحة ثابتين، أو لانهائي منتظم ( خط مستقيم فعلي)، إذا كان طول الحافة ثابتاً.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

خصائص عامة

Regular convex and star polygons with 3 to 12 vertices labelled with their Schläfli symbols

هذه الخصائص تنطبق على المضلعات المحدبة والنجمية.

جميع رؤوس المضلع المنتظم تقع على محيط دائرة.
لكل مضلع منتظم دائرة محيطة به ودائرة محاطة داخله.
من الممكن إنشاء مضلع منتظم له n ضلع باستخدام إنشاءات الفرجار والمسطرة فقط وفقط إذا كانت عوامل عدد أضلاعه الفردية والأولية هي أعداد فيرما. راجع المضلع القابل للإنشاء.

التماثل

إن مجموعة التناظر لمضلع منتظم من جانب n هو مجموعة ثنائية السطوح D_n (بالترتيب 2n): D₂، هي D₃، D₄، ... يتكون من التدويرات في C_n، جنباً إلى جنب مع تناظر الانعكاس في n من المحاور التي تمر عبر المركز. إذا كانت n زوجية، فإن نصف هذه المحاور تمر عبر رأسين متقابلين، والنصف الآخر يمر عبر نقطة منتصف الأضلاع المتقابلة. إذا كانت n فردية، فحينئذٍ تمر جميع المحاور من خلال قمة الرأس ونقطة المنتصف في الجانب المقابل.

المضلعات المحدبة المنتظمة

تكون جميع المضلعات البسيطة المنتظمة (المضلع البسيط هو الذي لا يتقاطع مع نفسه في أي مكان) محدبة. تلك التي لديها نفس العدد من الأضلاع هي أيضاً متشابهة.

يُرمز إلى المضلع المنتظم المحدب ذو الجوانب n بواسطة رمز شلفلي { n }. لـ {n}.n < 3، لدينا حالتان اضمحلال:

المضلع الأحادي {1}: الاضمحلال في الفضاء العادي. (لا تعتبر معظم الأقسام الأحادية مضلعاً حقيقياً، ويرجع ذلك جزئياً إلى هذا، وأيضًا لأن الصيغ أدناه لا تعمل، وبنيتها ليست أي مضلع مجردة.)
يضمحل المضلع الثنائي {2}، "مقطع ذو خط مزدوج": في الفضاء العادي. (بعض الأقسام لا تعتبر المضلع الثنائي مضلعاً حقيقياً بسبب هذا).

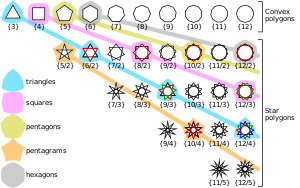
في سياقات معينة، ستكون جميع المضلعات التي يتم النظر فيها منتظمة. في مثل هذه الظروف، من المعتاد إسقاط البادئة العادية. على سبيل المثال، يجب أن تكون جميع أوجه متعدد السطوح المنتظم منتظمة وسيتم وصف الوجوه ببساطة على أنها مثلث، أو مربع، أو خماسي، إلخ.

الزوايا

للحصول على محدب منتظم n-gon، كل زاوية داخلية لها مقياس:

{\frac {180(n-2)}{n}}

درجة;

{\frac {(n-2)\pi }{n}}

راديان ; أو

{\frac {(n-2)}{2n}}

أدوار كاملة،

وكل زاوية خارجية (على سبيل المثال، المكملة للزاوية الداخلية) لها قياس ${\tfrac {360}{n}}$ درجة، بمجموع الزوايا الخارجية يساوي 360 درجة أو 2π راديان أو دورة كاملة واحدة.

عندما يقترب عدد الأضلاع n من اللانهاية، تقترب الزاوية الداخلية من 180 درجة. بالنسبة لمضلع منتظم به 10000 جانب (مضلع كثير الجوانب)، تكون الزاوية الداخلية 179.964 درجة. مع زيادة عدد الجوانب، يمكن أن تقترب الزاوية الداخلية جداً من 180 درجة، ويقترب شكل المضلع من شكل الدائرة. لكن المضلع لا يمكن أن يصبح دائرة. لا يمكن أن تصبح قيمة الزاوية الداخلية مساوية تماماً لـ 180 درجة، حيث سيصبح المحيط فعلياً خطاً مستقيماً. لهذا السبب، فإن الدائرة ليست مضلعاً له عدد لا نهائي من الأضلاع.

الأقطار

بالنسبة لـ n > 2، يكون عدد الأقطار هو ${\tfrac {1}{2}}n(n-3)$ ; i.e., 0, 2, 5, 9, ...، لمثلث، مربع، خماسي، مسدس، .... تقسم الأقطار المضلع إلى 1 ، 4 ، 11 ، 24 ، ... قطعة قالب:Oeis.

بالنسبة إلى n-gon المدرج في دائرة نصف قطرها وحدة، فإن حاصل ضرب المسافات من رأس معين إلى جميع الرؤوس الأخرى (بما في ذلك الرؤوس والرؤوس المجاورة المتصلة بقطر ما) يساوي n .

النقاط في المستوى

بالنسبة إلى n-gon البسيط المنتظم مع الدائرة المحيطة R والمسافات d_i من نقطة عشوائية في المستوى إلى الرؤوس، لدينا ^[1]

{\frac {\sum _{i=1}^{n}d_{i}^{4}}{n}}+3R^{4}=\left({\frac {\sum _{i=1}^{n}d_{i}^{2}}{n}}+R^{2}\right)^{2}.

لقوى مسافات أعلى $d_{i}$ من نقطة عشوائية في المستوى إلى رؤوس $n$ -gon منتظم، إذا

S_{n}^{(2m)}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2m}

,

إذاً^[2]

S_{n}^{(2m)}=(S_{n}^{(2)})^{m}+\sum _{k=1}^{\lfloor {\frac {m}{2}}\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R^{2k}(S_{n}^{(2)}-R^{2})^{k}(S_{n}^{(2)})^{m-2k}

,

و

S_{n}^{(2m)}=(S_{n}^{(2)})^{m}+\sum _{k=1}^{\lfloor {\frac {m}{2}}\rfloor }{\frac {1}{2^{k}}}{\binom {m}{2k}}{\binom {2k}{k}}(S_{n}^{(4)}-(S_{n}^{(2)})^{2})^{k}(S_{n}^{(2)})^{m-2k}

,

حيث $m$ هو عدد صحيح موجب أقل من $n$ .

إذا كانت $L$ هي المسافة من نقطة عشوائية في المستوى إلى النقطه الوسطى لخط منتظم $n$ -gon مع محيط نصف قطره $R$ ^[2]

\sum _{i=1}^{n}d_{i}^{2m}=n((R^{2}+L^{2})^{m}+\sum _{k=1}^{\lfloor {\frac {m}{2}}\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R^{2k}L^{2k}(R^{2}+L^{2})^{m-2k})

,

حيث $m$ = 1,2,…, $n$ -1.

النقاط الداخلية

بالنسبة إلى n-gon المنتظمة، فإن مجموع المسافات العمودية من أي نقطة داخلية إلى الجوانب n هي n مضروبة في العامد^[3]^{:p. 72}(العامد هو المسافة من المركز إلى أي جانب). هذا هو تعميم مبرهنة ڤيڤياني لحالة n=3 .^[4]^[5]

نصف القطر المحيط

مضلع خماسي منتظم (n = 5) مع الجانب s، الدائرة المحيطة R و العامد a

رسومات الجانب, s ; العامد, a و المساحة, A للمضلعات المنتظمة ذات n جانب و نصف قطر محيط 1، مع قاعدة، b لمستطيل بنفس المساحة – الخط الأخضر يبين الحالة n = 6

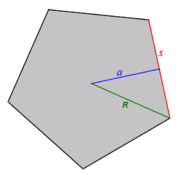
الدائرة المحيطة R من مركز مضلع منتظم إلى أحد الرؤوس مرتبطة بطول الضلع s أو بـ العامد a بواسطة

R={\frac {s}{2\sin \left({\frac {\pi }{n}}\right)}}={\frac {a}{\cos \left({\frac {\pi }{n}}\right)}}

بالنسبة إلى المضلعات القابلة للإنشاء، التعبيرات الجبرية لهذه العلاقات موجودة؛ راجع مضلع ثنائي المركز#المضلعات المنتظمة.

مجموع الخطوط العمودية من رؤوس n-gon المنتظمة إلى أي خط مماس للدائرة يساوي n مضروباً في الدائرة المحيطة.^[3]^{:p. 73}

مجموع المسافات المربعة من رؤوس n-gon المنتظمة إلى أي نقطة في محيطها تساوي 2nR² حيث R هي الدائرة المحيطة.^[3]^:p.73

مجموع المسافات المربعة من النقاط المتوسطة الجانبية لـn-gon المنتظم إلى أي نقطة على الدائرة المحيطة هو 2nR² − ns²/4، حيث s هو طول الضلع و R هو محيط نصف القطر.^[3]^{:p. 73}

إذا كانت $d_{i}$ هي المسافات من الرؤوس المنتظمة لـ $n$ -gon إلى أي نقطة في محيطها، إذاً ^[2]

3(\sum _{i=1}^{n}d_{i}^{2})^{2}=2n\sum _{i=1}^{n}d_{i}^{4}

.

التقطيعات

نص كوتكسر على أنه يمكن تشريح كل مضلع مركزي التماثل (2m-gon حيث تكون جوانبها المقابلة متوازية ومتساوية الطول) إلى ${\tbinom {n}{2}}$ أو m(m-1)/2 متوازي أضلاع. يتم احتواء هذه الأسقف كمجموعات فرعية من الرؤوس والحواف والوجوه في إسقاطات m-مكعب المتعامدة.^[6] وينطبق هذا بشكل خاص على المضلعات المنتظمة ذات الجوانب المتعددة بشكل متساوٍ، وفي هذه الحالة تكون جميع متوازيات الأضلاع معينية. تعطي القائمة OEIS: A006245 عدد الحلول للمضلعات الأصغر.

أمثلة لتقطيعات مختارة لمضلعات منتظمة زوجية الأضلاع
2m	6	8	10	12	14	16	18	20	24	30	40	50
الصورة
المعينات	3	6	10	15	21	28	36	45	66	105	190	300

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

المساحة

تُتعطى المساحة A لمضلع ذو n-حافة منتظم محدب له جانب s، دائرة محيطة R، عامد a و محيط p بواسطة^[7]^[8]

A={\tfrac {1}{2}}nsa={\tfrac {1}{2}}pa={\tfrac {1}{4}}ns^{2}\cot \left({\tfrac {\pi }{n}}\right)=na^{2}\tan \left({\tfrac {\pi }{n}}\right)={\tfrac {1}{2}}nR^{2}\sin \left({\tfrac {2\pi }{n}}\right)

بالنسبة للمضلعات المنتظمة التي يكون ضلعها s = 1، أو الدائرة المحيطة R = 1، أو العامد a = 1، ينتج عن ذلك الجدول التالي:^[9] (لاحظ أنه عندما يكون $\cot x\rightarrow 1/x$ كـ $x\rightarrow 0$ ,^[10] تميل المساحة $s=1$ إلى $n^{2}/4\pi$ حيث يتضخم $n$ .)

عدد الجوانب	المساحة عندما يكون الجانب s = 1		المساحة عندما تكون الدائرة المحيطة R = 1			المساحة عندما يكون العامد a = 1
عدد الجوانب	دقيق	تقريب	دقيق	تقريب	ككسر (تقريبي) من مساحة الدائرة المحيطة	دقيق	تقريب	ككسر (تقريبي) من المساحة الغير دائرية
n	${\tfrac {n}{4}}\cot \left({\tfrac {\pi }{n}}\right)$		${\tfrac {n}{2}}\sin \left({\tfrac {2\pi }{n}}\right)$		${\tfrac {n}{2\pi }}\sin \left({\tfrac {2\pi }{n}}\right)$	$n\tan \left({\tfrac {\pi }{n}}\right)$		${\tfrac {n}{\pi }}\tan \left({\tfrac {\pi }{n}}\right)$
3	${\tfrac {\sqrt {3}}{4}}$	0.433012702	${\tfrac {3{\sqrt {3}}}{4}}$	1.299038105	0.4134966714	$3{\sqrt {3}}$	5.196152424	1.653986686
4	1	1.000000000	2	2.000000000	0.6366197722	4	4.000000000	1.273239544
5	${\tfrac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}$	1.720477401	${\tfrac {5}{4}}{\sqrt {{\tfrac {1}{2}}\left(5+{\sqrt {5}}\right)}}$	2.377641291	0.7568267288	$5{\sqrt {5-2{\sqrt {5}}}}$	3.632712640	1.156328347
6	${\tfrac {3{\sqrt {3}}}{2}}$	2.598076211	${\tfrac {3{\sqrt {3}}}{2}}$	2.598076211	0.8269933428	$2{\sqrt {3}}$	3.464101616	1.102657791
7		3.633912444		2.736410189	0.8710264157		3.371022333	1.073029735
8	$2+2{\sqrt {2}}$	4.828427125	$2{\sqrt {2}}$	2.828427125	0.9003163160	$8\left({\sqrt {2}}-1\right)$	3.313708500	1.054786175
9		6.181824194		2.892544244	0.9207254290		3.275732109	1.042697914
10	${\tfrac {5}{2}}{\sqrt {5+2{\sqrt {5}}}}$	7.694208843	${\tfrac {5}{2}}{\sqrt {{\tfrac {1}{2}}\left(5-{\sqrt {5}}\right)}}$	2.938926262	0.9354892840	$2{\sqrt {25-10{\sqrt {5}}}}$	3.249196963	1.034251515
11		9.365639907		2.973524496	0.9465022440		3.229891423	1.028106371
12	$6+3{\sqrt {3}}$	11.19615242	3	3.000000000	0.9549296586	$12\left(2-{\sqrt {3}}\right)$	3.215390309	1.023490523
13		13.18576833		3.020700617	0.9615188694		3.204212220	1.019932427
14		15.33450194		3.037186175	0.9667663859		3.195408642	1.017130161
15	^[11]	17.64236291	^[12]	3.050524822	0.9710122088	^[13]	3.188348426	1.014882824
16	^[14]	20.10935797	$4{\sqrt {2-{\sqrt {2}}}}$	3.061467460	0.9744953584	^[15]	3.182597878	1.013052368
17		22.73549190		3.070554163	0.9773877456		3.177850752	1.011541311
18		25.52076819		3.078181290	0.9798155361		3.173885653	1.010279181
19		28.46518943		3.084644958	0.9818729854		3.170539238	1.009213984
20	^[16]	31.56875757	^[17]	3.090169944	0.9836316430	^[18]	3.167688806	1.008306663
100		795.5128988		3.139525977	0.9993421565		3.142626605	1.000329117
1000		79577.20975		3.141571983	0.9999934200		3.141602989	1.000003290
10,000		7957746.893		3.141592448	0.9999999345		3.141592757	1.000000033
1,000,000		79577471545		3.141592654	1.000000000		3.141592654	1.000000000

Comparison of sizes of regular polygons with the same edge length, from three to sixty sides. The size increases without bound as the number of sides approaches infinity.

من بين كل n-gons ذات محيط معين، يكون المضلع الذي يحتوي على أكبر مساحة منتظماً.^[19]

المضلع القابل للإنشاء

بعض المضلعات المنتظمة سهلة الإنشاء بالفرجار والمسطرة ؛ ولا يمكن إنشاء المضلعات المنتظمة الأخرى على الإطلاق. عرف علماء الرياضيات اليونانيون القدماء كيفية بناء مضلع منتظم به 3 أو 4 أو 5 جوانب،^[20]^{:p. xi} وقد عرفوا كيفية بناء مضلع منتظم مع ضعف عدد أضلاع مضلع منتظم معين.^[20]^{:pp. 49–50} أدى هذا إلى طرح السؤال: هل من الممكن بناء جميع n-gons المنتظمة بالفرجار والمسطرة؟ إذا لم يكن الأمر كذلك، فما هي n-gons القابلة للإنشاء وأيها ليست كذلك?

أثبت كارل فريدرك گاوس قابلية إنشاء 17-gon المنتظم في عام 1796. وقد قام بعد خمس سنوات، بتطوير نظرية الدورة الگاوسية في الاكتشافات الحسابية. سمحت له هذه النظرية بصياغة شرط كافٍ لإمكانية إنشاء المضلعات المنتظمة:

يمكن إنشاء n-gons باستخدام الفرجار والمسطرة إذا كان n هو جداء قوة 2 وأي عدد من أولية فيرما (بما في ذلك لا شيء).

(أولية فيرما هو عدد أولي بالشكل $2^{(2^{n})}+1.$ ) صرح گاوس بدون برهان على أن هذا الشرط كان أيضاً لازماً، لكنه لم يقوم بنشر برهانه. وقد تم تقديم برهان كامل على لزومية الشرط من قبل پيير وانتزل في عام 1837. والنتيجة معروفة باسم مبرهنة گاوس-وانتزل.

بالمقابل، يمكن إنشاء n-gons المنتظم إذا وفقط إذا كان جيب التمام لزاويته المشتركة عدد قابل للتكوين - أي يمكن كتابته من حيث العمليات الحسابية الأساسية الأربع واستخراج الجذور التربيعية.

المضلعات المنتظمة المتخالفة

يحتوي المكعب على انحراف منتظم سداسي، يُنظر إليه على أنه 6 حواف حمراء متعرجة بين مستويين متعامدين مع المحور القطري للمكعب.	تمثل الحواف الجانبية المتعرجة لـ n-موشور معاكس انحرافاً منتظماً لـ 2n-gon، كما هو موضح في هذا الموشور المعاكس ذو 17-gonal.

يمكن النظر إلى المضلع المنحرف في 3 فضاءات على أنها مسارات غير مستوية متعرجة بين مستويين متوازيين، تُعرّف على أنها الحواف الجانبية للموشور المعاكس. حيث تكون جميع الحواف والزوايا الداخلية متساوية.

يحتوي المجسم المثالي (رباعي السطوح و المكعب و المثمن و الاثناعشري و العشريني) على مضلعات پتري، تظهر باللون الأحمر هنا بجوانب 4 و 6 و 6 و 10 و 10 على التوالي.

بشكل عام، يمكن تعريف مضلعات الانحراف المنتظم في n-فضاء. تشمل الأمثلة مضلع پتري، المسارات متعددة الأضلاع للحواف التي تقسم كثير الجوانب المنتظم إلى نصفين، ويُنظر إليها على أنها مضلع منتظم في الإسقاط المتعامد.

في الحدود اللانهائية، تصبح المضلعات المنحرفة المنتظمة مضلعات لانهائية منحرفة.

المضلعات النجمية المنتظمة

2 < 2q < p, gcd(p, q) = 1

{5/2}	{7/2}	{7/3}...

{p/q}

p

q

مجموعة تناظر

Dihedral (D_p)

مضلع ثنوي

Self-dual

زاوية داخلية
(بالدرجات)

{\frac {180(p-2q)}{p}}

^[21]

المضلع المنتظم غير المحدب هو مضلع نجمي منتظم. المثال الأكثر شيوعاً هو النجمة الخماسية، التي لها نفس رؤوس الخماسي ، لكنه يربط الرؤوس المتناوبة.

بالنسبة إلى مضلع نجمي ذي n-جانب، يتم تعديل رمز شلفلي للإشارة إلى كثافة أو نجمية m في المضلع، مثل {n/m}. إذا كانت m تساوي 2، على سبيل المثال، يتم ضم كل نقطة ثانية. إذا كانت m تساوي 3، فسيتم ضم كل نقطة ثالثة. تتجه حدود المضلع حول مرات المركز m .

النجوم المنتظمة (غير المضمحلة) لما يصل إلى 12 جانب هي:

النجمة الخماسية – {5/2}
النجمة السباعية – {7/2} and {7/3}
النجمة الثمانية – {8/3}
النجمة التساعية – {9/2} و {9/4}
النجمة العشارية – {10/3}
نجمة إحدى عشرية – {11/2}, {11/3}, {11/4} و {11/5}
نجمة إثنى عشرية – {12/5}

يجب أن تكون m و n عددين أوليين مشتركين، وإلا فإن الشكل سوف يضمحل.

النجوم المنتظمة المضمحلة لما يصل 12 جانبًا هي:

الرباعيات – {4/2}
السداسيات – {6/2}, {6/3}
المثمنات – {8/2}, {8/4}
التساعيات – {9/3}
العشاريات – {10/2}, {10/4}, و {10/5}
عشرينيات – {12/2}, {12/3}, {12/4}, و {12/6}

تفسيران لـ {6/2}
گرون‌باوم {6/2} أو 2{3}^[22]	كوكستر 2{3} أو {6}[2{3}]{6}

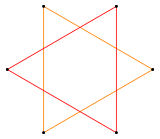
سداسي مضاعف اللف	نجمة سداسية كمركـَّب من مثلثين

اعتماداً على الاشتقاق الدقيق لرمز شلفلي، تختلف الآراء حول طبيعة الشكل المضمحل. على سبيل المثال، يمكن معاملة {6/2} بإحدى طريقتين:

في معظم فترات القرن العشرين (انظر على سبيل المثال Coxeter (1948))، أخذنا / 2 للإشارة إلى ربط كل رأس من رأس محدب {6} بجوارها القريب على بعد خطوتين، للحصول على مركب منتظم لمثلثين، أو نجمة سداسية.
يوضح كوكستر هذا المركب المنتظم بعلامة{kp}[k{p}]{kp} للمركب {p/k}، لذلك يتم تمثيل النجمة السداسية على شكل {6}[2{3}]{6}.^[23] كتب كوكستر أيضاً 2{n/2} بشكل أكثر إحكاماً، مثل 2{3} للنجمة السداسية كمركب مثل المتناوبات للمضلعات المنتظمة ذات الجوانب الزوجية، بخط مائل على العامل الرئيسي لتمييزه عن التفسير المتزامن.^[24]
تعتبر العديد من المقاييس الهندسية الحديثة، مثل گرون‌باوم(2003)،^[22] هذا غير صحيح. قانو بأخذ / 2 للإشارة إلى تحريك مكانين حول {6} في كل خطوة، للحصول على مثلث "مزدوج القطع" له رأسان متراكبان عند كل نقطة ركن وحافتين على طول كل مقطع خطي. ولا يتلاءم هذا بشكل أفضل مع النظريات الحديثة لـ كثير الجوانب مجرد فحسب، بل إنه ينسخ أيضاً بشكل أوثق الطريقة التي أنشأ بها پوانزوت (1809) مضلعاته النجمية - بأخذ طول واحد من الأسلاك وثنيها على التوالي من خلال نفس الزاوية حتى يغلق الشكل.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

ثنوية المضلعات المنتظمة

جميع المضلعات المنتظمة هي ذاتية-مزدوجة من أجل التطابق، وبالنسبة إلى n الفردية فهي ذاتية-مزدوجة.

بالإضافة إلى ذلك، فإن الأشكال النجمية المنتظمة (المركبات)، التي تتكون من مضلعات منتظمة، هي أيضاً ذاتية-مزدوجة.

المضلعات المنتظمة كأوجه لمتعددات الأسطح

يحتوي متعدد السطوح المنتظم على مضلعات منتظمة مثل الوجوه، بحيث يوجد تخطيط متساوي القياس لكل رأسين يرسم أحدهما إلى الآخر (تماماً كما هو الحال في المضلع المنتظم).

متعدد السطوح شبه دائري هو متعدد السطوح منتظم له نوعان فقط من الوجوه بالتناوب حول كل رأس.

متعدد السطوح المنتظم هو متعدد السطوح منتظم له نوع واحد فقط من الوجوه.

تُعرف الأجزاء المتبقية (غير المنتظمة) متعددة السطوح المحدبة ذات الوجوه المنتظمة باسم مجسمات جونسن.

متعدد السطوح له مثلثات منتظمة كوجوه ويسمى deltahedron.

انظر أيضاً

Euclidean tilings by convex regular polygons
Platonic solid
Apeirogon – An infinite-sided polygon can also be regular, {∞}.
List of regular polytopes and compounds
Equilateral polygon
دائرة كارلايل

الهامش

^ Park, Poo-Sung. "Regular polytope distances", Forum Geometricorum 16, 2016, 227-232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
^ ^أ ^ب ^ت Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355.
^ ^أ ^ب ^ت ^ث Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
^ Pickover, Clifford A, The Math Book, Sterling, 2009: p. 150
^ Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.
^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
^ "Math Open Reference". Retrieved 4 Feb 2014.
^ "Mathwords".

^ Results for R = 1 and a = 1 obtained with Maple, using function definition:

f := proc (n)
options operator, arrow;
[
 [convert(1/4*n*cot(Pi/n), radical), convert(1/4*n*cot(Pi/n), float)],
 [convert(1/2*n*sin(2*Pi/n), radical), convert(1/2*n*sin(2*Pi/n), float), convert(1/2*n*sin(2*Pi/n)/Pi, float)],
 [convert(n*tan(Pi/n), radical), convert(n*tan(Pi/n), float), convert(n*tan(Pi/n)/Pi, float)]
]
end proc

The expressions for n=16 are obtained by twice applying the tangent half-angle formula to tan(π/4)

^ Trigonometric functions
^ ${\tfrac {15}{8}}\left({\sqrt {15}}+{\sqrt {3}}+{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right)$
^ ${\tfrac {15}{16}}\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)$
^ ${\tfrac {15}{2}}\left(3{\sqrt {3}}-{\sqrt {15}}-{\sqrt {2\left(25-11{\sqrt {5}}\right)}}\right)$
^ $4\left(1+{\sqrt {2}}+{\sqrt {2\left(2+{\sqrt {2}}\right)}}\right)$
^ $16\left(1+{\sqrt {2}}\right)\left({\sqrt {2\left(2-{\sqrt {2}}\right)}}-1\right)$
^ $5\left(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {5}}}}\right)$
^ ${\tfrac {5}{2}}\left({\sqrt {5}}-1\right)$
^ $20\left(1+{\sqrt {5}}-{\sqrt {5+2{\sqrt {5}}}}\right)$
^ Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
^ ^أ ^ب Bold, Benjamin. Famous Problems of Geometry and How to Solve Them, Dover Publications, 1982 (orig. 1969).
^ Kappraff, Jay (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific. p. 258. ISBN 978-981-02-4702-7.
^ ^أ ^ب Are Your Polyhedra the Same as My Polyhedra? برانكو گرون‌باوم (2003), Fig. 3
^ Regular polytopes, p.95
^ Coxeter, The Densities of the Regular Polytopes II, 1932, p.53

المراجع

Coxeter, H.S.M. (1948). "Regular Polytopes". Methuen and Co. {{cite journal}}: Cite journal requires |journal= (help)
Grünbaum, B.; Are your polyhedra the same as my polyhedra?, Discrete and comput. geom: the Goodman-Pollack festschrift, Ed. Aronov et al., Springer (2003), pp. 461–488.
Poinsot, L.; Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9 (1810), pp. 16–48.

وصلات خارجية

Eric W. Weisstein, Regular polygon at MathWorld.
Regular Polygon description With interactive animation
Incircle of a Regular Polygon With interactive animation
Area of a Regular Polygon Three different formulae, with interactive animation
Renaissance artists' constructions of regular polygons at Convergence

v t e كثيرات الجوانب المعتادة والمنتظمة المحدبة الأساسية في الأبعاد 2–10
العائلة	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
مضلع منتظم	مثلث	مربع	p-gon	مسدس	مخمس
متعدد السطوح المنتظم	رباعي الأسطح	Octahedron • مكعب	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
المواضيع: Polytope families • Regular polytope • List of regular polytopes and compounds

الكلمات الدالة:

متعدد السطوح

[1] Park, Poo-Sung. "Regular polytope distances", Forum Geometricorum 16, 2016, 227-232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf

[Mamuka-2] أ ^ب ^ت Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355.

[Johnson-3] أ ^ب ^ت ^ث Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).

[4] Pickover, Clifford A, The Math Book, Sterling, 2009: p. 150

[5] Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.

[6] Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141

[7] "Math Open Reference". Retrieved 4 Feb 2014.

[8] "Mathwords".

[9] Results for R = 1 and a = 1 obtained with Maple, using function definition:
f := proc (n) options operator, arrow; [ [convert(1/4*n*cot(Pi/n), radical), convert(1/4*n*cot(Pi/n), float)], [convert(1/2*n*sin(2*Pi/n), radical), convert(1/2*n*sin(2*Pi/n), float), convert(1/2*n*sin(2*Pi/n)/Pi, float)], [convert(n*tan(Pi/n), radical), convert(n*tan(Pi/n), float), convert(n*tan(Pi/n)/Pi, float)] ] end proc
The expressions for n=16 are obtained by twice applying the tangent half-angle formula to tan(π/4)

[10] Trigonometric functions

[11] ${\tfrac {15}{8}}\left({\sqrt {15}}+{\sqrt {3}}+{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right)$

[12] ${\tfrac {15}{16}}\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)$

[13] ${\tfrac {15}{2}}\left(3{\sqrt {3}}-{\sqrt {15}}-{\sqrt {2\left(25-11{\sqrt {5}}\right)}}\right)$

[14] $4\left(1+{\sqrt {2}}+{\sqrt {2\left(2+{\sqrt {2}}\right)}}\right)$

[15] $16\left(1+{\sqrt {2}}\right)\left({\sqrt {2\left(2-{\sqrt {2}}\right)}}-1\right)$

[16] $5\left(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {5}}}}\right)$

[17] ${\tfrac {5}{2}}\left({\sqrt {5}}-1\right)$

[18] $20\left(1+{\sqrt {5}}-{\sqrt {5+2{\sqrt {5}}}}\right)$

[19] Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.

[Bold-20] أ ^ب Bold, Benjamin. Famous Problems of Geometry and How to Solve Them, Dover Publications, 1982 (orig. 1969).

[21] Kappraff, Jay (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific. p. 258. ISBN 978-981-02-4702-7.

[Branko-22] أ ^ب Are Your Polyhedra the Same as My Polyhedra? برانكو گرون‌باوم (2003), Fig. 3

[23] Regular polytopes, p.95

[24] Coxeter, The Densities of the Regular Polytopes II, 1932, p.53

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]



وبينار	مصادر	صور	الأخبار	فيديو