قيم ومتجهات ذاتية
القيمة الذاتية لنظام ما eigen value أو بالأحرى في معادلة تفاضلية هو عدد يمكن أن يكون من الأعداد الصحيحة أو من الأعداد المعقدة.
مقاربة الرياضيات التفاضلية للقيمة الذاتية
حساب حل معادلة تفاضلية من الدرجة الأولى:
فلنعتبر مثلا المعادلة التفاضلية البسيطة التالية(مع غض الطرف مبدئيا عن وجوب إعتبار الشروط الأولى أي initial conditions عند حساب الحل):
و لنحاول البحث عن حل هذه المعادلة. المعروف هو أنه يمكن أن نقول أن حل هذالمعادلة هو:
أي أن و إذا عوضت x ب فإنك تحصل على المعادلة التالية:
أي
أي بعد أن نشطب من المعادلة فإنك تحصل على المعادلة
و هذا بدوره يعني أن c=-10.
القيمة الذاتية
في عملية الحساب أعلاه وصلنا من معادلة تفاضلية من الدرجة الأولى إلى معادلة بسيطة لحساب القيمة الذاتية c ألا وهي المعادلة و يمكن تعميم هذه الطريقة أي كيفية الوصول من معادلة تفاضلية ذات درجة 2 أو 3 إلخ...إلى المعادلة لحساب القيمة الذاتية أو في هذه الحالة القيم الذاتية (لأن درجة العلاقة التفاضلية تتطابق دائما مع عدد القيم الخاصة التي تحسبها حيث يكون عليك في هذه الحالة حل بولينومات polynoms و أن تراعي طبعا أن بعض الحلول قد تكون مكررة أي أنه يجب أن تعدها عدة مرات حتى تكون ملاحظتي هذه صحيحة).
كما يجدر الإشارة إلى أن هذه الطريقة أو المعالجة حيث فقط للنظم أو المعادلات التفاضلية الخطية أي أنه في صورة إنعدام الخطية لا يمكن الحديث عن قيمة ذاتية.
كما أن القيمة الذاتية تعلمنا إذا كان نظام ما مستقرا (إذا كانت القيمة الذاتية سالبة) أو غير مستقر (إذا كانت القيمة موجبة). وهي كذلك دليل على سرعة النظام أو سرعة رده (إذا كانت القيمة المطلقة للقيمة الذاتية كبيرة فإن النظام سريع أي سرعة ردة فعله سريعة).
مقاربة الرياضيات الخطية للقيمة الذاتية
التطبيقات
القيم الذاتية للتحويلات الهندسية
The following table presents some example transformations in the plane along with their 2×2 matrices, eigenvalues, and eigenvectors.
| Scaling | Unequal scaling | Rotation | Horizontal shear | Hyperbolic rotation | |
|---|---|---|---|---|---|
| Illustration | 
|

|

|

| |
| Matrix | |||||
| Characteristic polynomial |
|||||
| Eigenvalues, | , | ||||
| Algebraic mult., |
|||||
| Geometric mult., |
|||||
| Eigenvectors | All nonzero vectors |
The characteristic equation for a rotation is a quadratic equation with discriminant , which is a negative number whenever θ is not an integer multiple of 180°. Therefore, except for these special cases, the two eigenvalues are complex numbers, ; and all eigenvectors have non-real entries. Indeed, except for those special cases, a rotation changes the direction of every nonzero vector in the plane.
A linear transformation that takes a square to a rectangle of the same area (a squeeze mapping) has reciprocal eigenvalues.
معادلة شرودنگر

An example of an eigenvalue equation where the transformation is represented in terms of a differential operator is the time-independent Schrödinger equation in quantum mechanics:
where , the Hamiltonian, is a second-order differential operator and , the wavefunction, is one of its eigenfunctions corresponding to the eigenvalue , interpreted as its energy.
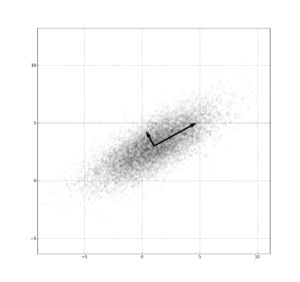
Principal component analysis
Vibration analysis
Eigenvalue problems occur naturally in the vibration analysis of mechanical structures with many degrees of freedom. The eigenvalues are the natural frequencies (or eigenfrequencies) of vibration, and the eigenvectors are the shapes of these vibrational modes. In particular, undamped vibration is governed by
or
that is, acceleration is proportional to position (i.e., we expect to be sinusoidal in time).
In dimensions, becomes a mass matrix and a stiffness matrix. Admissible solutions are then a linear combination of solutions to the generalized eigenvalue problem
where is the eigenvalue and is the (imaginary) angular frequency. The principal vibration modes are different from the principal compliance modes, which are the eigenvectors of alone. Furthermore, damped vibration, governed by
leads to a so-called quadratic eigenvalue problem,
This can be reduced to a generalized eigenvalue problem by algebraic manipulation at the cost of solving a larger system.
The orthogonality properties of the eigenvectors allows decoupling of the differential equations so that the system can be represented as linear summation of the eigenvectors. The eigenvalue problem of complex structures is often solved using finite element analysis, but neatly generalize the solution to scalar-valued vibration problems.
Eigenfaces

In image processing, processed images of faces can be seen as vectors whose components are the brightnesses of each pixel.[1] The dimension of this vector space is the number of pixels. The eigenvectors of the covariance matrix associated with a large set of normalized pictures of faces are called eigenfaces; this is an example of principal component analysis. They are very useful for expressing any face image as a linear combination of some of them. In the facial recognition branch of biometrics, eigenfaces provide a means of applying data compression to faces for identification purposes. Research related to eigen vision systems determining hand gestures has also been made.
Similar to this concept, eigenvoices represent the general direction of variability in human pronunciations of a particular utterance, such as a word in a language. Based on a linear combination of such eigenvoices, a new voice pronunciation of the word can be constructed. These concepts have been found useful in automatic speech recognition systems for speaker adaptation.
See also
- Antieigenvalue theory
- Eigenoperator
- Eigenplane
- Eigenvalue algorithm
- Introduction to eigenstates
- Jordan normal form
- List of numerical analysis software
- Nonlinear eigenproblem
- Quadratic eigenvalue problem
- Singular value
Notes
References
Citations
- ^ Xirouhakis, A.; Votsis, G.; Delopoulus, A. (2004), Estimation of 3D motion and structure of human faces, National Technical University of Athens, http://www.image.ece.ntua.gr/papers/43.pdf
Sources
- Akivis, Max A.; Goldberg, Vladislav V. (1969), Tensor calculus, Russian, Science Publishers, Moscow
- Aldrich, John (2006), "Eigenvalue, eigenfunction, eigenvector, and related terms", in Jeff Miller, Earliest Known Uses of Some of the Words of Mathematics, http://jeff560.tripod.com/e.html, retrieved on 2006-08-22
- Alexandrov, Pavel S. (1968), Lecture notes in analytical geometry, Russian, Science Publishers, Moscowقالب:ISBN?
- Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X, https://archive.org/details/firstcourseinlin0000beau
- Beezer, Robert A. (2006), A first course in linear algebra, Free online book under GNU licence, University of Puget Sound, http://linear.ups.edu/
- Betteridge, Harold T. (1965), The New Cassell's German Dictionary, New York: Funk & Wagnall
- Bowen, Ray M.; Wang, Chao-Cheng (1980), Linear and multilinear algebra, Plenum Press, New York, ISBN 0-306-37508-7
- Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3, https://archive.org/details/numericalanalysi00burd
- Carter, Tamara A.; Tapia, Richard A.; Papaconstantinou, Anne, Linear Algebra: An Introduction to Linear Algebra for Pre-Calculus Students, Rice University, Online Edition, http://ceee.rice.edu/Books/LA/index.html, retrieved on 2008-02-19
- Cohen-Tannoudji, Claude (1977), "Chapter II. The mathematical tools of quantum mechanics", Quantum mechanics, John Wiley & Sons, ISBN 0-471-16432-1
- Curtis, Charles W. (1999), Linear Algebra: An Introductory Approach (4th ed.), Springer, ISBN 0-387-90992-3
- Demmel, James W. (1997), Applied numerical linear algebra, SIAM, ISBN 0-89871-389-7
- Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
- Fraleigh, John B.; Beauregard, Raymond A. (1995), Linear algebra (3rd ed.), Addison-Wesley Publishing Company, ISBN 0-201-83999-7
- Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E. (1989), Linear algebra (2nd ed.), Englewood Cliffs, NJ: Prentice Hall, ISBN 0-13-537102-3
- Gelfand, I. M. (1971), Lecture notes in linear algebra, Russian, Science Publishers, Moscow
- Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2005), Indefinite linear algebra and applications, Basel, Boston, Berlin: Birkhäuser Verlag, ISBN 3-7643-7349-0
- Golub, Gene F.; van der Vorst, Henk A. (2000), "Eigenvalue computation in the 20th century", Journal of Computational and Applied Mathematics 123 (1–2): 35–65, doi:, Bibcode: 2000JCoAM.123...35G
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix computations (3rd ed.), Baltimore, MD: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
- Greub, Werner H. (1975), Linear Algebra (4th ed.), New York: Springer-Verlag, ISBN 0-387-90110-8
- Halmos, Paul R. (1987), Finite-dimensional vector spaces (8th ed.), New York: Springer-Verlag, ISBN 0-387-90093-4
- Hawkins, T. (1975), "Cauchy and the spectral theory of matrices", Historia Mathematica 2: 1–29, doi:
- Hefferon, Jim (2001), Linear Algebra, Colchester, VT: Online book, St Michael's College, http://joshua.smcvt.edu/linearalgebra/
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Horn, Roger A.; Johnson, Charles F. (1985), Matrix analysis, Cambridge University Press, ISBN 0-521-30586-1
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Oxford University Press, ISBN 0-19-501496-0
- Korn, Granino A.; Korn, Theresa M. (2000), "Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review", New York: McGraw-Hill (Dover Publications), ISBN 0-486-41147-8, Bibcode: 1968mhse.book.....K
- Kuttler, Kenneth (2007), An introduction to linear algebra, Brigham Young University, http://www.math.byu.edu/~klkuttle/Linearalgebra.pdf
- Lancaster, P. (1973), Matrix theory, Russian, Moscow: Science Publishers
- Larson, Ron; Edwards, Bruce H. (2003), Elementary linear algebra (5th ed.), Houghton Mifflin Company, ISBN 0-618-33567-6
- Lipschutz, Seymour (1991), Schaum's outline of theory and problems of linear algebra, Schaum's outline series (2nd ed.), New York: McGraw-Hill Companies, ISBN 0-07-038007-4
- Meyer, Carl D. (2000), Matrix analysis and applied linear algebra, Philadelphia: Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley
- (in روسية)Pigolkina, T. S.; Shulman, V. S. (1977). "Eigenvalue". In Vinogradov, I. M. (ed.). Mathematical Encyclopedia. Vol. 5. Moscow: Soviet Encyclopedia.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), Numerical Recipes: The Art of Scientific Computing (3rd ed.), ISBN 978-0521880688
- Roman, Steven (2008), Advanced linear algebra (3rd ed.), New York: Springer Science + Business Media, ISBN 978-0-387-72828-5
- Sharipov, Ruslan A. (1996), Course of Linear Algebra and Multidimensional Geometry: the textbook, ISBN 5-7477-0099-5, Bibcode: 2004math......5323S
- Shilov, Georgi E. (1977), Linear algebra, Translated and edited by Richard A. Silverman, New York: Dover Publications, ISBN 0-486-63518-X
- Shores, Thomas S. (2007), Applied linear algebra and matrix analysis, Springer Science+Business Media, ISBN 978-0-387-33194-2
- Strang, Gilbert (1993), Introduction to linear algebra, Wellesley, MA: Wellesley-Cambridge Press, ISBN 0-9614088-5-5
- Strang, Gilbert (2006), Linear algebra and its applications, Belmont, CA: Thomson, Brooks/Cole, ISBN 0-03-010567-6
External links
الوصلات الخارجية في هذه المقالة قد تكون غير متبعة لسياسات المحتوى في المعرفة أو تعليماتها. فضلاً طور هذه المقالة بإزالة الوصلات الخارجية غير المناسبة أو الزائدة. (December 2019) |
- What are Eigen Values? – non-technical introduction from PhysLink.com's "Ask the Experts"
- Eigen Values and Eigen Vectors Numerical Examples – Tutorial and Interactive Program from Revoledu.
- Introduction to Eigen Vectors and Eigen Values – lecture from Khan Academy
- Hill, Roger (2009). "λ – Eigenvalues". Sixty Symbols. Brady Haran for the University of Nottingham.
- "A Beginner's Guide to Eigenvectors". Deeplearning4j. 2015. Archived from the original on 2018-07-21. Retrieved 2015-08-18.
- Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10 – A visual explanation with 3Blue1Brown
- Matrix Eigenvectors Calculator from Symbolab (Click on the bottom right button of the 2x12 grid to select a matrix size. Select an size (for a square matrix), then fill out the entries numerically and click on the Go button. It can accept complex numbers as well.)
Theory
- Hazewinkel, Michiel, ed. (2001), "Eigen value", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Hazewinkel, Michiel, ed. (2001), "Eigen vector", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Eigenvalue (of a matrix) على بلانيت ماث
- Eigenvector – Wolfram MathWorld
- Eigen Vector Examination working applet
- Same Eigen Vector Examination as above in a Flash demo with sound
- Computation of Eigenvalues
- Numerical solution of eigenvalue problems Edited by Zhaojun Bai, James Demmel, Jack Dongarra, Axel Ruhe, and Henk van der Vorst
- Eigenvalues and Eigenvectors on the Ask Dr. Math forums: [1], [2]



