استقرار

الإستقرار Stability في الرياضيات هي حالة من حالات الأنظمة أو بتعبير آخر هي خاصية رياضية عادة ما تذكر إقترانا بحل معادلة تفاضلية حيث يقال حل المعادلة التفاضلية كذا و كذا مستقر أو غير مستقر.

Mathematics

Stability theory, the study of the stability of solutions to differential equations and dynamical systems
Stability (probability), a property of probability distributions
Stability (learning theory), a property of machine learning algorithms
Stability, a property of sorting algorithms
Numerical stability, a property of numerical algorithms which describes how errors in the input data propagate through the algorithm
Stability radius, a property of continuous polynomial functions
Stable theory, concerned with the notion of stability in model theory
Stability, a property of points in geometric invariant theory
K-Stability, a stability condition for algebraic varieties.
Bridgeland stability conditions, a class of stability conditions on elements of a triangulated category.
Stability (algebraic geometry)

Engineering

In atmospheric fluid dynamics, atmospheric stability, a measure of the turbulence in the ambient atmosphere
BIBO stability (Bounded Input, Bounded Output stability), in signal processing and control theory
Directional stability, the tendency for a body moving with respect to a medium to point in the direction of motion
Elastic stability, the resistance of a structural member to buckling
Flight dynamics, including longitudinal stability
Nyquist stability criterion, defining the limits of stability for pole-zero analysis in control systems
Relaxed stability, the property of inherently unstable aircraft
Ship stability in naval architecture includes
- Limit of positive stability, the angle at which a boat will no longer stay upright
- Stability conditions (watercraft) of waterborne vessels
Slope stability, a property of soil-covered slopes
Stability model of software design

Natural sciences

Band of stability, in physics, the scatter distribution of isotopes that do not decay
Chemical stability, occurring when a substance is in a dynamic chemical equilibrium with its environment
- Thermal stability of a chemical compound
- Kinetic stability of a chemical compound
- Stability constants of complexes, in solution
Convective instability, a fluid dynamics condition
Ecological stability, measure of the probability of a population returning quickly to a previous state, or not going extinct
Plasma stability, a measure of how likely a perturbation in a plasma is to be damped out

Exercise and sports medicine

Core stability of the abdominal muscles
Joint stability in the musculoskeletal system

Social sciences

Economic stability, the absence of excessive fluctuations in the macroeconomy
Hegemonic stability theory, a theory of international relations
Mertens-stable equilibrium, called "stability" in game theory
Political stability

Entertainment

The Stability EP, a 2002 three song EP by Death Cab for Cutie
"Stability", a song by Debbie Harry from the album Debravation
"Stability" (short story), by Philip K. Dick

الأنظمة الخطية و الإستقرار

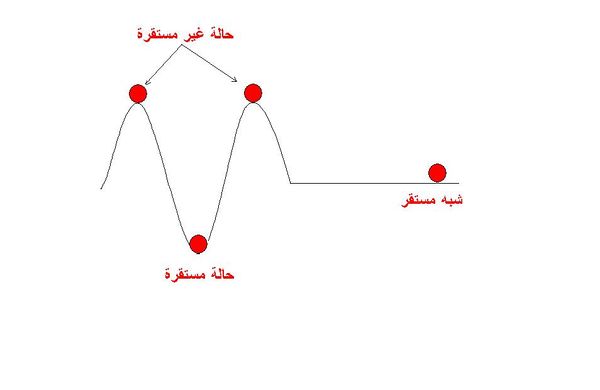
بالنسبة للأنظمة الخطية أو المعادلات التفاضلية الخطية يجب على القيمة الذاتية أن تكون سالبة أو بالأحرى إذا سلمنا بأن القيمة الذاتية هي عدد مركب فإنه يجب أن يكون جزئه الحقيقي سالبا. إذا كان الجزء الحقيقي صفرا فإن النظام يسمى شبه مستقر أي أنه لا يعود إلى حالته السابقة إذا قمنا بتغييرها تغييرا طفيفا بل يبقى في الحالة التي وضعناه فيها. أما النظام المستقر فيعود إلى حالته الأولى إذا أبعدناه عنها إبعادا طفيفا. النظام الغير مستقر يبتعد أكثر فأكثر من حالته الأولية إذا أبعدناه عنها. الصورة أسفله مثلا ترمز لكرة متحركة على أسطح مختلفة وتبين إختلاف خاصية إستقرار الوضعية حسب الأرضية. رياضيا يدرس هذا المثال باشتقاق نموذج هو عبارة عن معادلة تمثل حركة الكرة ثم تتم دراسة إستقراره حسب الطرائق المبينة أسفله.

الأنظمة الغير خطية و الإستقرار

بالنسبة للأنظمة الغير خطية من نوع:
${\displaystyle{\displaystyle{\dot{x}}=f(x,u)}}$
حيث f دالة غير خطية و x ، u شعاعان, يصعب حساب القيمة الذاتية أو أن مفهوم القيمة الذاتية غير متعارف عليه في هذه الأنظمة. في هذه الحالة تكون أحد الطرق التي يمكن من خلالها معرفة إن كان نظام ما مستقر أم لا هو الإستعانة بمبرهنة ليابونوف. و قبل تبيين طريقة ليابونوف لدراسة الإستقرار فإنه يجدر بالذكر أنه يمكن تخطيط النظام (linearisation) أو المعادلة في نقطة معينة ${\displaystyle{\displaystyle x_{l},u_{l}}}$ و حساب القيمة الذاتية لهذا النظام الخطي فيها و على أساس القيمة الذاتية المتحصل عليها نقول أن النظام مستقر أم لا. المشكل الوحيد هو أن تصنيفنا هذا للنظام ليس صحيحا إلا في دائرة ضيقة حول نقطة التخطيط, أي أنه مثلا إذا قلنا أن النظام مستقر فهذا يعني أنه مستقر في النقطة ${\displaystyle{\displaystyle x_{l},u_{l}}}$ و بعض النقاط حولها و لكن لا نعرف حجم المجال الذي يضم هذه النقاط

مبرهنة ليابونوف

تقول مبرهنة ليابونوف الآتي:
إذا كان لدينا نظام نعبر عنه كالآتي
${\displaystyle{\displaystyle{\begin{bmatrix}{\dot{x}}_{1}\\ {\dot{x}}_{2}\\ \vdots\\ {\dot{x}}_{n}\end{bmatrix}}={\begin{bmatrix}{f}_{1}(x_{1},\ldots,x_{n},u_{1})% \\ {f}_{2}(x_{1},\ldots,x_{n},u_{2})\\ \vdots\\ {f}_{n}(x_{1},\ldots,x_{n},u_{n})\end{bmatrix}}}}$
و إذا كانت لهذا النظام نقطة سكون (stady state) نسميها مثلا ${\displaystyle{\displaystyle{x}_{R}}}$ فإن نقطة السكون هذه مستقرة إذا أمكننا إيجاد دالة تسمى دالة ليابونوف و هي دالة تتوفر فيها المواصفات التالية:

${\displaystyle{\displaystyle V(x_{1},...,X_{n})>0}}$ أي ما يعرف رياضيا ب تحدد موجب Positiv definit أي أن الدالة V لا تكون صفرا إلا عند النقطة صفر ${\displaystyle{\displaystyle{\underline{0}}}}$ (أو حالة السكون التي يمكن بتحويل خطي بسيط translation نقلها من النقطة ${\displaystyle{\displaystyle X_{r}}}$ إلى النقطة صفر.) وفي ما عدا ذلك أكبر من الصفر.

${\displaystyle{\displaystyle{\dot{V}}=(gradV(x))^{T}.{\dot{x}}<0}}$ أي أن تفاضل الدالة الرياضية يجب أن يكون سالبا في ما عدا النقطة صفر ${\displaystyle{\displaystyle{\underline{0}}}}$ . أي أن تفاضل الدالة تتميز بخاصية التحدد السالب negative definit.

في حالة تمكنا من العثور على مثل هذه الدالة فإن النظام مستقر. و لنلاحظ هنا أن إستعمال هذه الطريقة لا يقتصر على الأنظمة الخطية بل يمكن أيضا إستعمالها في الأنظمة الغير الخطية. كما يجدر بالذكر أنه في حالة عدم عثورنا على هذه الدالة فإنه لا يمكننا أن نجزم بأن النظام ${\displaystyle{\displaystyle{\dot{x}}=f(x)}}$ غير مستقر بل ما نستنتجه هو أن الدالة التي إخترناها لبرهنة الإستقرار لا تصلح لذلك و يجب علينا إختيار أخرى لهذا الغرض. أي أنه لا يمكننا بطريقة ليابونوف أن نبرهن على عدم إستقرار نظام ما و لكن يمكننا أن نبرهن على إستقراره

الإستقرار المحلي

الإستقرار المحلي هو عندما تكون خاصية الإستقرار مرتبطة بمدى أو مجال رياضي معين تكون خارجه منتفية. لاجظ الصورة: الكرة وسط الهضبتين.

الإستقرار الشامل

أن تكون خاصية الإستقرار غير مرتبطة بمجال رياضي معين.

شبه إستقرار

شبه الإستقرار هي الحالة المبينة في الصورة و التي تعني أن نظاما ما لا يعود إلا نقطة إنطلاقه إذا أبعدته منها بل يظل في النقطة التي دفعته إليها. يمكن تبسيطا إعتبار هذه الحالة مستقرة لكن في الحقيقة هذه الحالة يمكن أن تكون مستقرة أو غير مستقرة ( أنظر نظرية الفضاء المحوري Center manifold Theory)

مواضيع متصلة

إستقرار رقمي numerical stability
إستقرار بنيوي structural stability

Other uses

Stability (wine)