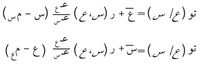تحليل الانكفاء

(تم التحويل من تحليل الارتباط)

تحليل الانحدار أو تحليل الارتباط Regression analysis هو كل طريقة إحصائية يتم فيها التنبؤ بمتوسط متغير عشوائي أو عدة متغيرات عشوائية اعتمادا على قيم وقياسات متغيرات عشوائية أخرى، له عدة أنواع مثل: الانحدار الخطي، والانحدار المنطق رمزي، وانحدار بواسون، والتعليم المراقب والانحدار الموزون الوحدة.

تحليل الانحدار هو أكثر من عملية ملائمة منحنى (أي اختيار المنحنى الكثر ملائمة لمجموعة نقاط بيانية معطاة) فهو يتضمن ملائمة نموذج باستخدام مكونات حتمية واعتباطية. المكونات الحتمية تدعى المتنبئات أما المكونات الاعتباطية فتدعى الخطأ.[1]


الشكل الأبسط لنموذج الانحدار يحوي متغير تابع (غير مستقل) (يدعى أيضا متغير الخرج، أو المتغير الداخلي أو المتغير-ع) إضافة إلى متغير مستقل (يدعى العامل، أو المتغير الخارجي، أو المتغير-س).

من الأمثلة النموذجية على تحليل الانحدار: اعتماد ضغط الدم Y على عمر الشخص X، أو اعتماد الوزن لحيوانات التجربة Y على معدل التغذية اليومي X. هذا الارتباط والتابعية بين X وY هي ما ندعوه بالانحدار أو الارتباط فنقول ارتباط Y ب X.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

التعريف

الانكفاء، هو طريقة للبحث عن علاقة ذات شكل مختار مسبقاً، تعبِّر عن الارتباط بين متغير ع يسمى المتغير التابع، ومتغير أو متغيرات أخرى س1، س2،... تسمى المتغيرات المستقلة. وقد يسمى ع متغيراً موصوفاً وتسمى س1،س2،... متغيرات واصفة. وهذه الأخيرة ليست دائماً مستقلة.

تحليل الانكفاء1.jpg

إن العلاقة القائمة بين ع والمتغيرات س1،س2،... التي يُعبَّر عنها بـ ع = تا (س1، س2،...)، تعرّف منحنياً أو سطحاً يسمح من أجل قيم مفروضة لـ س1،س2،... ، بتقدير قيمة ع بارتيابات عشوائية لا يمكن التعبيرعنها بدقة، بدلالة المتغيرات س1،س2،...

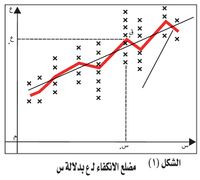
في حال متغيريْن ملاحظيْن س،ع يُمثل الارتباط الوسطي ع بدلالة س (انكفاء ع بدلالة س)، بمجموعة من النقط نى ذات الإحداثيات (سى،عى)، حيث: يكون عى متوسط قيم ع الموافقة لقيمة معينة لـ س=سى. و يُمثل «الخط المضلعي» الواصل بين هذه النقط (حين تتغير س) انكفاء ع بدلالة س. وإذا ما أمكن تقريب هذا الخط المضلعي إلى منحنٍ بارتياب مقبول دُعي هذا المنحني «منحني الانكفاء».


التاريخ

ظهر مصطلح الانكفاء أو الارتداد أو التراجع أول مرة في بحوث فرانسيس گالتون (1822-1911) في دراسته موضوع الوراثة. فَعِنْدَ عقد مقارنة بين أطول مجموعة من الآباء وأطوال أبنائهم خلُص إلى النتيجة التالية: يميل الأبناء لآباء مُفرطين في الطول إلى أن يكونوا أقصر من آبائهم، ويميل الأبناء لآباء مُفرطين في القصر إلى أن يكونوا أطول من آبائهم. وهذا يعني أن السلالات المتعاقبة لآباء بطول مفرط أو بقصر مفرط تنزع إلى الطول الوسطي للمجتمع. ومن هنا شاع تعبير الانكفاء الذي ما زال مستخدماً حتى اليوم. وفي عام 1925 اقترح ألكسندر روڤيتش تشوپروڤ (1874-1926)، مصطلحاً بديلاً، هو «العلاقة العشوائية»، وهذا يتوافق على نحو أفضل مع الخصائص العشوائية للارتباط المدروس مهما تكن الظاهرة المفروضة، ولكن هذا التعبير غير مستخدم عملياً.

أنواع الانكفاء

الانكفاء الخطي

يقال إن الانكفاء خطي إذا أمكن تسوية الخط المضلعي للانكفاء بمستقيم، وتكتب معادلة هذا المستقيم، في هذه الحالة، بالصيغة: ع=أ+ب س،، كما يمكن أن تكتب بالصيغة: 0ع(س)=ع+ب(س-س)، حيث تعطى ب ، وتسمى معامل الانكفاء، بالعلاقة: الانكفاء الخطي.jpg ويعطي هذا المعامل وسطياً، فكرةً عن تأثير تغيرات س على ع انطلاقاً من مجموعة المشاهدات. كذلك على نحو مماثل يمكن كتابة معادلة مستقيم الانكفاء لـ س بدلالة ع. إن هذين المستقيمين اللذين يمران من النقطة المتوسطة ن(س،ع) هما بوجه عام مختلفان، ولا يتطابقان إلا في الحال التي تقع فيها النقط نى على استقامة واحدة (وهي حال الارتباط الخطي التام بين المتغيريْن).

مستقيم الانكفاء لع بدلالة س.

ولتعيين مستقيمات الانكفاء تُستخدم طريقة «المربعات الأصغرية»، فمستقيم الانكفاء هو ذاك المستقيم الذي يجعل مجموع المربعات أصغرياً

المربعات الأصغرية.jpg

، وذلك بفرض أن نى نَى قطعة مستقيمة موازية لأحد المحورين الإحداثيين وأن نَى تقع على مستقيم الانكفاء. فإذا كان المطلوب مستقيم الانكفاء لـ ع بدلالة س كان:

الانكفاء الخطي2.jpg

يسمى مربع معامل الانكفاء الخطي س بدلالة ع «مُعامل التحديد» وهو يعطى بالعلاقة: الانكفاء الخطي3.jpg

ويمثل المقدار

مقدار التباين الكلي.jpg

التباين الكلي، و

التباين المفسر.jpg

التباين المفسَّر explained variation، ويحسب هذا من معادلة الانكفاء الخطي.

أما إذا فُرض أن المتغير ع تابع لعدة متغيرات س1،س2،... ، فان فرضية الانكفاء الخطي المتعدد تقود إلى البحث، بطريقة المربعات الأصغرية، عن معادلة انكفاء من الصيغة: ع(س1،س2،... )=أ+ب1س1+ب2س2+... حيث تبين معاملات الانكفاء الجزئية ب1،ب2،... أثر تغيّر كل من المتغيرات س1،س2،... في المتغير ع على التوالي. وتعرِّف المعادلة الأخيرة مستوى انكفـاءٍ في فضـاء ذي (ن + 1) بعداً. ويُعيّن مستوى الانكفاء ع بدلالة س1،س2،... بحيث يكون مجموع مربعات المسافات الموازية إلى م ع بين نقط المشاهدة والمستوي أصغرياً. ويقيس مُعاملُ الارتباط ر أو معامل التحديد ر2: معامل التحديد ر2.jpg

قوة العلاقة بين القيم الملاحظة للمتغير ع والقيم المقابلة المقدرة من معادلة مستوي الانكفاء.

الانكفاء المنحني

يقال إن الانكفاء منحنٍ إذا أمكن التعبير عن القيم الملاحظة لـ ع بدلالة واحد أو أكثر من المتغيرات، بدالّة (تابع) غير خطية لهذه المتغيرات.

من المسائل المطروحة في الإحصاء النظري حالة متغيرين س ، ع عُلِمتْ دالة الكثافة الاحتمالية المشتركة لهما. إن منحني الانكفاء ع بدلالة س في هذه الحال هو مجموعة النقط ذات الإحداثيات [س،تو(ع/س)] حيث يكون تو(ع/س) التوقع الرياضي (أو القيمة الوسطى) لـ ع في التوزيع الشرطي لـ ع من أجل قيمة ما لـ س ( س= س) ويعرَّف كذلك منحني الانكفاء لـ س بدلالة ع. ويعرَّفُ، في حال دالة كثافة لـ ن (عدد المتغيرات) متغيراً وبطريقة مماثلة، سطحُ انكفاء ذو ن + 1 بعداً.

وتبرز أهمية الانكفاء الخطي في حال التوزيع الطبيعي لمتغيرين (وهي حالة شائعة الحدوث)، ويمثَّل مستقيما الانكفاء عندئذ بالمعادلتين:

الانكفاء المنحني.jpg

حيث تتوالى الوسطاء مس، مع، عـس، عـع كما يلي: المتوسطان الحسابيان، والانحرافان المعياريان للتوزيعيين الهامشيين لـ س وع . وأما ر(س،ع) فهو معامل الارتباط لهذين المتغيرين. ويقال الشيء نفسه في حال توزيع طبيعي في ن متغيراً إذ تكون سطوح الانكفاء في هذه الحال مستويات.

انظر أيضاً


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

المصادر

  1. ^ محمد شفيق ياسين. "الانكفاء". الموسوعة العربية. Retrieved 2012-06-18.
  • Audi, R., Ed. (1996). "curve fitting problem," The Cambridge Dictionary of Philosophy. Cambridge, Cambridge University Press. pp.172-173.
  • William H. Kruskal and Judith M. Tanur, ed. (1978), "Linear Hypotheses," International Encyclopedia of Statistics. Free Press, v. 1,
Evan J. Williams, "I. Regression," pp. 523-41.
Julian C. Stanley, "II. Analysis of Variance," pp. 541-554.
  • Lindley, D.V. (1987). "Regression and correlation analysis," New Palgrave: A Dictionary of Economics, v. 4, pp. 120-23.
  • Birkes, David and Yadolah Dodge, Alternative Methods of Regression. ISBN 0-471-56881-3
  • Chatfield, C. (1993) "Calculating Interval Forecasts," Journal of Business and Economic Statistics, 11. pp. 121-135.
  • Draper, N.R. and Smith, H. (1998).Applied Regression Analysis Wiley Series in Probability and Statistics
  • Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage
  • Hardle, W., Applied Nonparametric Regression (1990), ISBN 0-521-42950-1
  • Meade, N. and T. Islam (1995) "Prediction Intervals for Growth Curve Forecasts," Journal of Forecasting, 14, pp. 413-430.
  • Munro, Barbara Hazard (2005) "Statistical Methods for Health Care Research" Lippincott Williams & Wilkins, 5th ed.
  • Gujarati, Basic Econometrics, 4th edition
  • Sykes, A.O. "An Introduction to Regression Analysis" (Inaugural Coase Lecture)
  • S. Kotsiantis, D. Kanellopoulos, P. Pintelas, Local Additive Regression of Decision Stumps, Lecture Notes in Artificial Intelligence, Springer-Verlag, Vol. 3955, SETN 2006, pp. 148 – 157, 2006
  • S. Kotsiantis, P. Pintelas, Selective Averaging of Regression Models, Annals of Mathematics, Computing & TeleInformatics, Vol 1, No 3, 2005, pp. 66-75
  • N. Cressie (1996) Change of Support and the Modiable Areal Unit Problem. Geographical Systems 3:159-180.
  • A.S. Fotheringham, C. Brunsdon, and M. Charlton. (2002) Geographically weighted regression: the analysis of spatially varying relationships. Wiley.
  • A.S. Fotheringham and D. Wong. (1991) The modifiable areal unit problem in multivariate statistical analysis. Environment and Planning A, 23(1):1025-1044.
  • Radchenko S.G. (2005) Robust methods for statistical models estimation: Monograph. — Кiev: РР «Sanspariel», 2005 — 504 p ISBN 966-96574-0-7 (on russian language)

برامج حاسوب

All major statistical-software packages perform the common types of regression analysis correctly and in a user-friendly way. Simple linear regression can be done in some spreadsheet applications. There are a number of software programs that perform specialized forms of regression, and experts may choose to write their own code to using statistical programming languages or numerical analysis software.

  • In Microsoft Excel LINEST spread sheet function performs linear regression analysis with optional calculation of confidence intervals.

وصلات خارجية

مشاع المعرفة فيه ميديا متعلقة بموضوع [[commons: Category:Regression analysis

| Regression analysis

]].


الكلمات الدالة:
تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=تحليل_الانكفاء&oldid=1406586"