إنحراف معياري

في الإحصاء ونظرية الإحتمالات يعتبر الانحراف المعياري Standard deviation القيمة الأكثر استخداما من بين مقاييس التشتت الإحصائي لقياس مدى التبعثر الإحصائي، أي أنه يدل على مدى امتداد مجالات القيم ضمن مجموعة البياننات الإحصائية .
و"التباين " Variance وهو معدل مربعات انحرافات العلامات في التوزيع عن الوسط الحسابي. ويكون الانحراف المعياري Standard deviation عندها الجذر التربيعي للتباين بالنسبة لمجموعة البيانات الإحصائية .
يتأثر التباين أو الانحراف المعياري بالقيم المتباعدة أو المتطرفة ولكنه لا يتأثر كثيرا بالتغيرات التي تطرأ على العينة, كما أنهما يرتبطان بالوسط الحسابي للتوزيع، بمعنى ان التشتت الذي نعبر عنه بالتباين أو الانحراف المعياري ينسب إلى الوسط الحسابي وليس لاي نقطة أخرى في التوزيع.
مثال على حساب الانحراف المعياري
سنأخذ هذا المثال البسيط على حساب الانحراف المعياري لكل من الرقمين 8 و4.
الخطوة 1: إحسب الـمتوسط حسابي للرقمين.
الخطوة 2: احسب انحراف كل من الرقمين السابقين عن الـمتوسط حسابي.
الخطوة 3: قم بتربيع الانحرافين:
الخطوة 4: إجمع التربيعين الناتجين:
الخطوة 5: قم بتقسيم الناتج على عدد القيم (وهو في مثالنا 2):
الخطوة 6: قم بإيجاد الجذر التربيعي الموجب:
إذاً الانحراف المعياري هو 2.
حساب الانحراف المعياري لمتغير
نفرض أن لدينا المتحولات (أو المتغيرات)، يعطى الانحراف المعياري لهذه القيم بالعلاقة:
حيث أن N هو عدد المتحولات (المتغيرات). ويمكن تبسيط العبارة السابقة إلى التالي:
يمكن البرهنة على ذلك بواسطة العملية الجبرية التالية:
بما أن علم الإحصاء يحلل و يعرص البيانات المتفرقة بحيث تكون ذات معنى معين أو تعطي انطباعا معيناً فان تباين هذه البيانات يمثل مشكله كبيرة في فهم سلوك البيانات.
التشتت
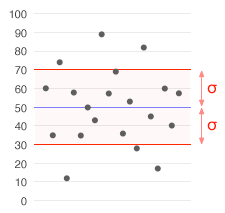
لشرح معنى التشتت يمكن أن نقدم المثال البسيط التالي: بالنظر للمفردات: ٩, ١٠, ١١ فأن وسطها الحسابي هو ١٠ و هو أفضل قيمة تصلح لتمثيل هذه المجموعة, لكن بالنظر إلى: ٨, ١٠, ١٢ فان وسطهم الحسابي هو أيضا ١٠ و كذلك ٦, ١٠, ١٤ أي أن الوسط الحسابي فقط لا يكفي لتعريف مجموعة البيانات بشكل دقيق بل نحتاج لمعيار اضافي يوضح مدى تشتت هذه البيانات حول الوسط الاحصائي و لذلك اقترح الاحصائيون ادخال مفهوم الانحراف المعياري و غيره من القيم التي تعبر عن مدى تشتت البيانات.
قواعد للبيانات الموزرعة اعتيادياً
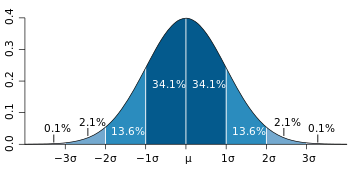
The central limit theorem says that the distribution of a sum of many independent, identically distributed random variables tends towards the normal distribution.
If a data distribution is approximately normal then about 68% of the values are within 1 standard deviation of the mean (mathematically, μ ± σ, where μ is the arithmetic mean), about 95% of the values are within two standard deviations (μ ± 2σ), and about 99.7% lie within 3 standard deviations (μ ± 3σ). This is known as the 68-95-99.7 rule, or the empirical rule.
For various values of z, the percentage of values expected to lie in the symmetric confidence interval (−zσ,zσ) are as follows:
| zσ | النسبة المئوية |
|---|---|
| 1σ | 68.2689492% |
| 1.645σ | 90% |
| 1.960σ | 95% |
| 2σ | 95.4499736% |
| 2.576σ | 99% |
| 3σ | 99.7300204% |
| 3.2906σ | 99.9% |
| 4σ | 99.993666% |
| 5σ | 99.9999426697% |
| 6σ | 99.9999998027% |
| 7σ | 99.9999999997440% |
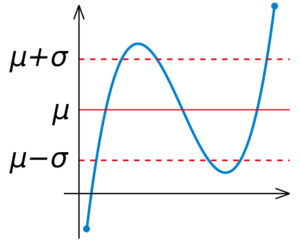
العلاقة بين الانحراف المعياري والمتوسط
انظر أيضاً
|
|
المصادر
وصلات خارجية
- A Guide to Understanding & Calculating Standard Deviation
- Interactive Demonstration and Standard Deviation Calculator
- Standard Deviation - an explanation without maths
- Standard Deviation, an elementary introduction
- Standard Deviation, a simpler explanation for writers and journalists
- Standard Deviation Calculator
- Texas A&M Standard Deviation and Confidence Interval Calculators