رياضيات الاستمثال
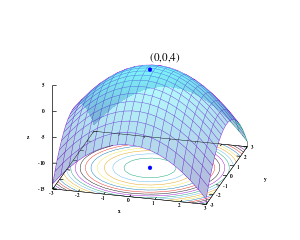
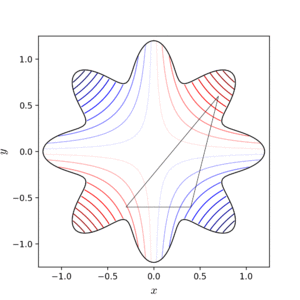
في الرياضيات ، مصطلح الاستمثال أو مفاضلية أو تحسين Optimization يشير إلى دراسة مسائل من الشكل التالي:
إذا كان لدينا : دالة رياضية f : A R من مجموعة A إلى مجموعة الأعداد الحقيقية. فإنه لدينا : عنصر x0 في A بحيث أن f(x0) ≤ f(x) من أجل جميع قيم x في المجموعة A ("تصغير" minimization ) أو بحيث أن f(x0) ≥ f(x) من أجل جميع قيم x في المجموعة A ("تكبير" maximization ).
مثل هذه الصياغة ندعوها أحيانا : برنامج رياضي mathematical program ، و هو مصطلح لا يرتبط ببرمجة الحاسب ، لكنه يبقى مستخدما في مجالات مثل البرمجة الخطية linear programming ، فائدة هذا الحقل الدراسي تكمن في قدرته على نمذجة العديد من المسائل النظرية و الواقعية أيضا .
A تؤلف مجموعة جزئية ما من الفضاء الإقليدي Rn, غالبا ما حدد عن طريق مجموعة من المحددات محددات constraints, أو المعادلات أو المتراجحات التي يجب أن تحققها عناصر A .
ficken alter عناصر A تدعى حلولا ممكنة (محتملة) feasible solutions . و الدالة f تدعى دالة موضوعية objective function أو دالة الكلفة cost function . الحل الممكن الذي يقوم بتصغير أو تكبير الدالة الموضوعية (حسب الغالية التي نريدها) ندعوه الحل الأمثل (الأفضل أو الأحسن) optimal solution .
نطاق الدالة f : وهو A يدعى فضاء البحث search space ، في حين تدعى عناصر A الحلول المرشحة candidate solution أو الحلول الممكنة feasible solutions .
بشكل عام ، يكون هناك عدة نهايات صغرى محلية local minima و نهايات عظمى maxima محلية ، حيث تعرف النهاية الصغرى المحلية x* على انها نقطة تحقق : من أجل بعض القيم δ > 0 و جميع قيم x التي تحقق :
- ;
تكون الصيغة التالية محققة :
هذا يعني أنه على أي نطاق كروي محيط ب x* تكون جميع قيم الدالة أكبر أو تساوي قيمة الدالة في هذه النقطة (هذا مفهوم النهاية الصغرى) . بشكل مشابه يمكننا تعريف النهاية العظمى و الكبيرة .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التعلم الآلي
برمجيات الحل
انظر أيضاً
- Brachistochrone
- Curve fitting
- Deterministic global optimization
- Goal programming
- Important publications in optimization
- Least squares
- Mathematical Optimization Society (formerly Mathematical Programming Society)
- Mathematical optimization algorithms
- Mathematical optimization software
- Process optimization
- Simulation-based optimization
- Test functions for optimization
- Variational calculus
- Vehicle routing problem
الهامش
للاستزادة
- Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization. Cambridge: Cambridge University Press. ISBN 0-521-83378-7.
- Gill, P. E.; Murray, W.; Wright, M. H. (1982). Practical Optimization. London: Academic Press. ISBN 0-12-283952-8.
- Lee, Jon (2004). A First Course in Combinatorial Optimization. Cambridge University Press. ISBN 0-521-01012-8.
- Nocedal, Jorge; Wright, Stephen J. (2006). Numerical Optimization (2nd ed.). Berlin: Springer. ISBN 0-387-30303-0.
- Snyman, J. A.; Wilke, D. N. (2018). Practical Mathematical Optimization : Basic Optimization Theory and Gradient-Based Algorithms (2nd ed.). Berlin: Springer. ISBN 978-3-319-77585-2.
وصلات خارجية
- "Decision Tree for Optimization Software". Links to optimization source codes
- "Global optimization".
- "EE364a: Convex Optimization I". Course from Stanford University.
- Varoquaux, Gaël. "Mathematical Optimization: Finding Minima of Functions".


