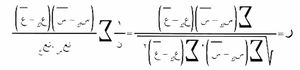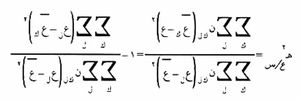الارتباط

فئات عديدة من (النقاط x, y)، بمعامل الارتباط لـ x و y لكل فئة. لاحظ أن الارتباط يعكس الضوضاء واتجاه العلاقة الخطية (الصف العلوي)، ولكن ليس ميل تلك العلاقة (الأوسط)، ولا العديد من أوجه العلاقات غير الخطية (الأسفل). ملحوظة: الشكل في المركز له ميل صفري، ولكن في تلك الحالة فإن معامل الارتباط غير معرّف لأن تباين Y هو صفر.

الارتباط correlation هو العلاقة القائمة بين متغيرين قابلين للقياس يلاحظان في آن واحد على كل مفردةٍ أو وحدةٍ من وحدات المجموعة الإِحصائية، ويمكن توسيع هذا المفهوم ليشمل العلائق الرابطة بين الخصائص الكيفية للظواهر.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

لمحة تاريخية

يعود الفضل الأول في دراسة مفهوم الارتباط للسير فرانسيس گالتون Sir Francis Galton (1822-1911) مؤسس المدرسة البيولوجية الإِنكليزية، التي عُرفت بهذا الاسم في عام 1881 من بحوثها في الصفات الوراثية.

وتوطدت بعد ذلك نظرية الارتباط بفضل أبحاث الرياضيين والمناطقة حتى كارل پيرسون Karl Pearson (1857-1936) واودني يول Udny Yule (1871-1951) وجون مينارد كينز John Maynard Keynes (1883-1916) ولاسيما ألكسندر ألكسندروڤيتش تشوپروڤ Alexander Alexandrovitch Tchoprov (1874-1926) الذي أطلق في عام 1925 على الارتباط اسم الصلات العشوائية بين المتغيرات التصادفية stochastic liaison of aleatary variables.

ومنذ تلك الحقبة ظهرت أعمال كثيرة أغنت الدراسة النظرية للارتباط قام بها علماء فرنسيون منهم جورج دارموا Georges Darmois (1888-1960) ورينيه ريسر René Risser (1869-1958) وموريس فريشيه Maurice Frechet (1878-1973).

دراسة الارتباط

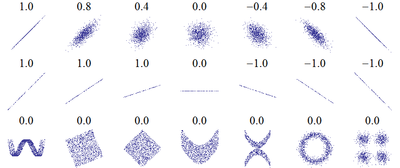
إِن الهدف الأساسي من تحليل الارتباط هو إِيجاد صيغة ملائمة لتعيين قوة العلاقة بين متغيرين عشوائيين س وع. ويدرس الارتباط ابتداءً من توزيع هذين المتغيرين، أي من جدولٍ ذي مأخذين يمثِّل كلُّ زوج مرتَّب من القيم (س،ع) عدد الوحدات الإِحصائية التي يأخذها المتغيران س و ع، أي التي يكون من أجلها س=س و ع=ع في آن واحد. ويمكن القيام بتمثيل بياني يقابل فيه كلُّ زوج مرتب (س،ع) بنقطةٍ في مستوي المحورين م س و م ع فتتشكل غمامة من النقط ذات الإِحداثيين (س،ع) تتكون منها فكرة عامة عن طبيعة العلاقة القائمة بين المتغيرين س و ع. وعندما تكون المتغيرات مستمرة يتمّ تجزئة مجالاتها إِلى فئات صغيرة إِن أمكن، ثم تُمثّل كل فئةٍ بقيمتها المركزية.

وتبرز من الوجهة النظرية حالتان حديتان:

أما الحالة الأولى فهي وجود علاقة دالِّية تامة بين المتغيرين (والعلاقة الدالِّية التامة هي العلاقة الممثلة بدقة بمعادلة جبرية كعلاقة محيط الدائرة بنصف قطرها).

تقابل فيها كل قيمة لـ(س=س) قيمة وحيدة لـ(ع=ع) مهما تكن الوحدات الإِحصائية الملاحظة، وهذه العلاقة الدالِّية هي علاقة تبادلية، وهذا يعني أن كل قيمة لـ(ع=ع) يقابلها قيمة وحيدة لـ(س=س).

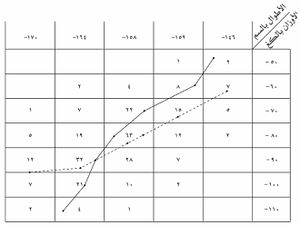
وأما الحالة الثانية فهي وجود استقلال بين المتغيرات، ويُقبل في هذه الحالة أن جميع التوزيعات الشرطية [والتوزيع الشرطي لمتغير ما مثل س هو مجموعة قيم ع الموافقة لقيمةٍ ما لـ(س=س)] الخاصة بأحد المتغيرين، من أجل قيمةٍ ما للآخر، تكون متطابقة ومطابقة للتوزيع الهامشي الموافق. وهذا يعني أن لهذه التوزيعات متوسطاً واحداً، وانحرافاً معيارياً واحداً. وفي هذه الحالة لاتقدم معرفة أحد المتغيرين س (أو ع) أية معلومات إضافية تتعلق بـ ع(أو س). وإِضافة إِلى هاتين الحالتين الحديتين، العلاقات التامة والاستقلال المطلق، هناك عدد غير منته من الحالات الوسطية بينهما يُطلق عليها اسم الارتباط أو العلاقات العشوائية وهذا مايُلحظ في الجدول التالي الممثَّل لتوزيع عدد من الأفراد بحسب ظاهرتي الطول مقدراً بالسنتيمتر والوزن مقدراً بالكيلو غرام.

يشير هذا الجدول إِلى وجود ارتباطٍ مابين الطول والوزن، ففي الخط المنقط تتوضع قيم ع في مراكز الفئات المقابلة لها. وفي الخط المتصل تقابل قيم س مراكز الفئات الموافقة لها.

قياس الارتباط

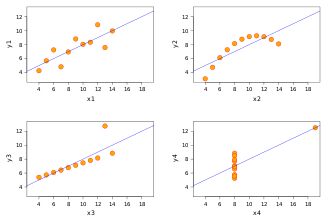
تقاس درجة ارتباط متغيرين بسعة انتشار نقط العيِّنة حول مستقيم الانكفاء[ر] فالشكل (أ) يمثل ارتباطاً تاماً، أما الشكل (ب) فيمثل ارتباطاً ضعيفاً. وفي حالة فقدان الارتباط بين س و ع يكون مستقيم الانكفاء أفقياً، وهذا يشير إِلى أن قيم ع مستقلةٌ عن قيم س الشكل (جـ). ويمكن أن تُطرح في هذا السياق المسألتان التاليتان:

الأولى: كيف يُدَلّ عددياً على وجود ارتباط بين متغيرين باستخدام مؤشر أو مُعامل يقيس أهمية العلاقة القائمة بينهما.
الثانية: في حالة وجود مثل هذه العلاقة، يطلب البحث عن معادلة تسمح بتقدير قيمة أحد المتغيرين بدلالة الآخر (وهذه هي مسألة الانكفاء). وقد استوحى كارل بيرسون Karl Pearson في عام 1896 من أعمال أوگست براڤيه August Bravais (1811-1863)، التي أنجزها عام 1846 في موضوع نظرية الأخطاء، تعريفاً لمعامل الارتباط يُعطى بالعلاقة التالية:

إِذ يمتد المجموع على جميع الثنائيات (س ك،ع ك) الملاحظة، أما س وع فترمزان إِلى المتوسطين الحسابيين للتوزعين الهامشيين و نع س، نع ع للانحرافين المعياريين لهما. ويعرف هذا المُعامل باسم مُعامل الارتباط correlation coefficient لـ برافي- بيرسون (Bravais-Pearson) أو مُعامل الارتباط الخطي، وهو ينتمي للمجال [-1،1] ويأخذ القيمتين ±1 عندما تقوم بين المتغيرين علاقة تامة. أما الإِشارة ± فتدل على اتجاه تحول أحد المتغيرين مع تغير الآخر، إِن الحالة ر=0 لاتعني فقدان الارتباط بالمعنى الذي ذُكر آنفاً إِنما تفيد أن مستقيمات الانكفاء المنشأة بطريقة المربعات الأصغرية (من أجل القيم س≠ع) توازي المحاور الإِحداثية. إِن مُعامل الارتباط الخطي ليس له أهمية تذكر إِلا في الحالة التي تصادف فيها علاقات خطية على وجه التقريب بين متوسطات التوزيعات الشرطية بأحد المتغيرات والقيم المقابلة للمتغير المرتبط به.

في عام 1901 اقترح بيرسون (Pearson) أيضاً تعريفاً لنسبة الارتباط correlation ratio يتوقف، من أجل كل متغير، على تباين المتوسطات الشرطية لهذا المتغير حول متوسطه العام.

وهكذا يمكن أن يدلل على ارتباط ع بـ س وفق العلاقة:

ن ك ل هو عدد المشاهدات التي يكون من أجلها س=س ك و ع=ع ك في آن واحد عك . متوسط التوزيع الشرطي لـ ع من أجل س=س ك، وتنعدم نسبة الارتباط هـ2ع/س إٍذا ساوت جميعُ المتوسطات الشرطية عك لـ ع من أجل س=س ك المتوسط العام ع، وفي هذه الحالة لا تتوقف هذه المتوسطات على س. كما أن نسبة الارتباط تساوي الواحد إِذا كانت جميع قيم ع، من أجل كل توزيع شرطي يقابل س=س ك، مساوية للمتوسط الشرطي ع=عك (العلاقة تامة بين المتوسطات).

التعميم

يمكن حساب مُعامل الارتباط في الحالة التي تفترض وجود أكثر من متغيرين آنيين. فإِذا قبلنا بوجود علاقات خطية تقريبية بين أي من المتغيرات والمتغيرات الأخرى، أمكن انطلاقاً من العلاقات المتبادلة بين المجموعات المختلفة لهذين المتغيرين، حساب مُعامل الارتباط الجزئي، أي دراسة الارتباط بين متغيرين بحذف تأثير المتغيرات الأخرى، أو حساب مُعامل الارتباط المتعدد، أي دراسة الارتباط لمتغيرٍ ما بدلالة مجموعة المتغيرات الأخرى.

Correlation	Negative	Positive
Small	−0.3 to −0.1	0.1 to 0.3
Medium	−0.5 to −0.3	0.3 to 0.5
Large	−1.0 to −0.5	0.5 to 1.0

الارتباط والسببية

إِن ارتباط ع بـ س لا يعني بالضرورة أن الظاهرة الممثَّلة بالمتغير ع تُفسَّر بالظاهرة س. إِذ إِن العلاقة بينهما، التي تصفها معادلة الانكفاء ليست سوى علاقة إِحصائية. فمن الممكن إِيجاد علاقة بين الإِنفاق الأُسري، أي المتغير المرتبط، ومقدار الدخل، أي المتغير المستقل، على الرغم من أن توافر المال لايعني بالضرورة إِنفاقه، فالإِنفاق هو قرار ذاتي يمكن أن يُتخذ في حال توافر المال، وإِن كان لا يحدث بالضرورة.

إِن الطبيعة العميقة لمسائل السببية لا تُستوحى من حساب مُعامل الارتباط الذي يوفر فقط دليلاً لتوجيه الدراسة.

يؤدي تحليل الارتباط خدمات كبيرة في مجالات عدة تستحيل فيها الطريقة التجريبية، كما في الدراسات الحيوية والنفسية والعلوم الاقتصادية التطبيقية، كما تسمح بإِيضاح الأوضاع التي تبدو مبهمة بسبب العدد الكبير من العوامل المؤثرة.

إِن التحليل العواملي الذي يبحث في تفسير الصلات القائمة بين الكثير من المتغيرات الملاحظة على الوحدة الإحصائية نفسها، بمساعدة عددٍ منته من العوامل المستقلة، يبنى على تحليل الارتباطات ر ك ل(ك≠ل=1، 2، 3، ...، ن) المحسوبة من أجل هذه المتغيرات على كل مفردةٍ من مفردات المجموعة.

أربع فئات من البيانات بنفس الارتباط البالغ 0.816

وقد نتجت هذه الدراسة من أعمال تشارلز إِدوارد سبيرمان Charles Edward Spearman (1863-1945) الذي قدم في بداية هذا القرن توصيفاً لظاهرة الذكاء لفردٍ ما ذي دلالة عالية المستوى باستخدام أقل عدد ممكن من المفردات. وشاع استخدام هذا التحليل اليوم في علم النفس التطبيقي (نظرية الروائز) كما أصبح يستخدم على نطاق واسع في مجالات متنوعة كما في الكيمياء الفيزيائية، وعلم الاجتماع وتحليل أسباب بعض التأثيرات الدوائية.

الارتباط الجغرافي

الارتباط أو المضاهاة correlation، هو الربط بين الوحدات الطبقية المتباعدة جغرافيا، ويشمل ذلك :-^[1]

ربط الوحدات الصخرية على أساس الامتداد الجانبي للنوعية الصخرية في مناطق قريبة مكشوفة (مضاهاة صخرية).
ربط الوحدات الصخرية على اساس محتواها الحفري (مضاهاة حيوية)، محليا وإقليميا وعالميا.
ربط الوحدات الصخرية على أساس تشابه العمر (مضاهاة زمنية) محليا وإقليميا وعالميا.
ربط الوحدات الصخرية، على أساس البصمة المغناطيسية القديمة (مضاهاة مغناطيسية طبقية) محليا وإقليميا.

انظر أيضاً

المصادر

^ عبد الجليل هويدي، محمد أحمد هيكل (2004). أساسيات الجيولوجيا التاريخية. مكتبة الدار العربية للكتب.

الموسوعة العربية

قراءات اخرى

Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .