عدد فيرما
| سُمي على اسم | Pierre de Fermat |
|---|---|
| عدد المصطلحات المعروفة | 5 |
| Conjectured number of terms | 5 |
| Subsequence of | Fermat numbers |
| أول المصطلحات | 3, 5, 17, 257, 65537 |
| أكبر مصطلح معروف | 65537 |
| OEIS index | A019434 |
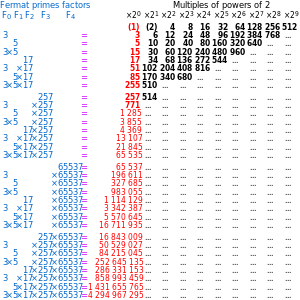
في الرياضيات، عدد فيرما سمي على اسم پيير فيرما الذي كان أول من درس هذه الأعداد. عدد فيرما هو عدد صحيح موجب من الشكل:
حيث n هو عدد صحيح غير سالب. ويمكن سرد أعداد فيرما التسعة الأولى كالتالي:
| F0 | = | 21 | + | 1 | = | 3 | |
| F1 | = | 22 | + | 1 | = | 5 | |
| F2 | = | 24 | + | 1 | = | 17 | |
| F3 | = | 28 | + | 1 | = | 257 | |
| F4 | = | 216 | + | 1 | = | 65,537 | |
| F5 | = | 232 | + | 1 | = | 4,294,967,297 | |
| = | 641 × 6,700,417 | ||||||
| F6 | = | 264 | + | 1 | = | 18,446,744,073,709,551,617 | |
| = | 274,177 × 67,280,421,310,721 | ||||||
| F7 | = | 2128 | + | 1 | = | 340,282,366,920,938,463,463,374,607,431,768,211,457 | |
| = | 59,649,589,127,497,217 × 5,704,689,200,685,129,054,721 | ||||||
| F8 | = | 2256 | + | 1 | = | 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,937 | |
| = | 1,238,926,361,552,897 × 93,461,639,715,357,977,769,163,558,199,606,896,584,051,237,541,638,188,580,280,321 |
إذا كان العدد 2n + 1 هو عدد أولي و كان n > 0 من الممكن برهان أن n هو من مضاعفات العدد 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الخصائص الأساسية
The Fermat numbers satisfy the following recurrence relations:
for n ≥ 1,
for n ≥ 2. Each of these relations can be proved by mathematical induction. From the second equation, we can deduce Goldbach's theorem (named after Christian Goldbach): no two Fermat numbers share a common integer factor greater than 1. To see this, suppose that 0 ≤ i < j and Fi and Fj have a common factor a > 1. Then a divides both
and Fj; hence a divides their difference, 2. Since a > 1, this forces a = 2. This is a contradiction, because each Fermat number is clearly odd. As a corollary, we obtain another proof of the infinitude of the prime numbers: for each Fn, choose a prime factor pn; then the sequence {pn} is an infinite sequence of distinct primes.
المزيد من الخصائص
- No Fermat prime can be expressed as the difference of two pth powers, where p is an odd prime.
- With the exception of F0 and F1, the last digit of a Fermat number is 7.
- The sum of the reciprocals of all the Fermat numbers (المتتالية A051158 في OEIS) is irrational. (Solomon W. Golomb, 1963)
Primality
Fermat numbers and Fermat primes were first studied by Pierre de Fermat, who conjectured that all Fermat numbers are prime. Indeed, the first five Fermat numbers F0, ..., F4 are easily shown to be prime. Fermat's conjecture was refuted by Leonhard Euler in 1732 when he showed that
Euler proved that every factor of Fn must have the form k2n+1 + 1 (later improved to k2n+2 + 1 by Lucas) for n ≥ 2.
That 641 is a factor of F5 can be deduced from the equalities 641 = 27 × 5 + 1 and 641 = 24 + 54. It follows from the first equality that 27 × 5 ≡ −1 (mod 641) and therefore (raising to the fourth power) that 228 × 54 ≡ 1 (mod 641). On the other hand, the second equality implies that 54 ≡ −24 (mod 641). These congruences imply that 232 ≡ −1 (mod 641).
Fermat was probably aware of the form of the factors later proved by Euler, so it seems curious that he failed to follow through on the straightforward calculation to find the factor.[1] One common explanation is that Fermat made a computational mistake.
There are no other known Fermat primes Fn with n > 4, but little is known about Fermat numbers for large n.[2] In fact, each of the following is an open problem:
- Is Fn composite for all n > 4?
- Are there infinitely many Fermat primes? (Eisenstein 1844)[3]
- Are there infinitely many composite Fermat numbers?
- Does a Fermat number exist that is not square-free?
اعتبارا من 2014[تحديث], it is known that Fn is composite for 5 ≤ n ≤ 32, although of these, complete factorizations of Fn are known only for 0 ≤ n ≤ 11, and there are no known prime factors for n = 20 and n = 24.[4] The largest Fermat number known to be composite is F18233954, and its prime factor 7 × 218233956 + 1 was discovered in October 2020.
Heuristic arguments
Heuristics suggest that F4 is the last Fermat prime.
The prime number theorem implies that a random integer in a suitable interval around N is prime with probability 1/ln N. If one uses the heuristic that a Fermat number is prime with the same probability as a random integer of its size, and that F5, ..., F32 are composite, then the expected number of Fermat primes beyond F4 (or equivalently, beyond F32) should be
One may interpret this number as an upper bound for the probability that a Fermat prime beyond F4 exists.
This argument is not a rigorous proof. For one thing, it assumes that Fermat numbers behave "randomly", but the factors of Fermat numbers have special properties. Boklan and Conway published a more precise analysis suggesting that the probability that there is another Fermat prime is less than one in a billion.[5]
Equivalent conditions
Let be the nth Fermat number. Pépin's test states that for n > 0,
- is prime if and only if
The expression can be evaluated modulo by repeated squaring. This makes the test a fast polynomial-time algorithm. But Fermat numbers grow so rapidly that only a handful of them can be tested in a reasonable amount of time and space.
There are some tests for numbers of the form k2m + 1, such as factors of Fermat numbers, for primality.
- Proth's theorem (1878). Let = + with odd < . If there is an integer such that
- then is prime. Conversely, if the above congruence does not hold, and in addition
- (See Jacobi symbol)
- then is composite.
If N = Fn > 3, then the above Jacobi symbol is always equal to −1 for a = 3, and this special case of Proth's theorem is known as Pépin's test. Although Pépin's test and Proth's theorem have been implemented on computers to prove the compositeness of some Fermat numbers, neither test gives a specific nontrivial factor. In fact, no specific prime factors are known for n = 20 and 24.
Factorization
Because of Fermat numbers' size, it is difficult to factorize or even to check primality. Pépin's test gives a necessary and sufficient condition for primality of Fermat numbers, and can be implemented by modern computers. The elliptic curve method is a fast method for finding small prime divisors of numbers. Distributed computing project Fermatsearch has found some factors of Fermat numbers. Yves Gallot's proth.exe has been used to find factors of large Fermat numbers. Édouard Lucas, improving Euler's above-mentioned result, proved in 1878 that every factor of the Fermat number , with n at least 2, is of the form (see Proth number), where k is a positive integer. By itself, this makes it easy to prove the primality of the known Fermat primes.
Factorizations of the first twelve Fermat numbers are:
F0 = 21 + 1 = 3 is prime F1 = 22 + 1 = 5 is prime F2 = 24 + 1 = 17 is prime F3 = 28 + 1 = 257 is prime F4 = 216 + 1 = 65,537 is the largest known Fermat prime F5 = 232 + 1 = 4,294,967,297 = 641 × 6,700,417 (fully factored 1732 [6]) F6 = 264 + 1 = 18,446,744,073,709,551,617 (20 digits) = 274,177 × 67,280,421,310,721 (14 digits) (fully factored 1855) F7 = 2128 + 1 = 340,282,366,920,938,463,463,374,607,431,768,211,457 (39 digits) = 59,649,589,127,497,217 (17 digits) × 5,704,689,200,685,129,054,721 (22 digits) (fully factored 1970) F8 = 2256 + 1 = 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,
639,937 (78 digits)= 1,238,926,361,552,897 (16 digits) ×
93,461,639,715,357,977,769,163,558,199,606,896,584,051,237,541,638,188,580,280,321 (62 digits) (fully factored 1980)F9 = 2512 + 1 = 13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,393,377,723,561,443,721,764,0
30,073,546,976,801,874,298,166,903,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,6
49,006,084,097 (155 digits)= 2,424,833 × 7,455,602,825,647,884,208,337,395,736,200,454,918,783,366,342,657 (49 digits) ×
741,640,062,627,530,801,524,787,141,901,937,474,059,940,781,097,519,023,905,821,316,144,415,759,
504,705,008,092,818,711,693,940,737 (99 digits) (fully factored 1990)F10 = 21024 + 1 = 179,769,313,486,231,590,772,930...304,835,356,329,624,224,137,217 (309 digits) = 45,592,577 × 6,487,031,809 × 4,659,775,785,220,018,543,264,560,743,076,778,192,897 (40 digits) ×
130,439,874,405,488,189,727,484...806,217,820,753,127,014,424,577 (252 digits) (fully factored 1995)F11 = 22048 + 1 = 32,317,006,071,311,007,300,714,8...193,555,853,611,059,596,230,657 (617 digits) = 319,489 × 974,849 × 167,988,556,341,760,475,137 (21 digits) × 3,560,841,906,445,833,920,513 (22 digits) ×
173,462,447,179,147,555,430,258...491,382,441,723,306,598,834,177 (564 digits) (fully factored 1988)
اعتبارا من نوفمبر 2021[تحديث], only F0 to F11 have been completely factored.[4] The distributed computing project Fermat Search is searching for new factors of Fermat numbers.[7] The set of all Fermat factors is A050922 (or, sorted, A023394) in OEIS.
The following factors of Fermat numbers were known before 1950 (since then, digital computers have helped find more factors):
| Year | Finder | Fermat number | Factor |
|---|---|---|---|
| 1732 | Euler | ||
| 1732 | Euler | (fully factored) | |
| 1855 | Clausen | ||
| 1855 | Clausen | (fully factored) | |
| 1877 | Pervushin | ||
| 1878 | Pervushin | ||
| 1886 | Seelhoff | ||
| 1899 | Cunningham | ||
| 1899 | Cunningham | ||
| 1903 | Western | ||
| 1903 | Western | ||
| 1903 | Western | ||
| 1903 | Western | ||
| 1903 | Cullen | ||
| 1906 | Morehead | ||
| 1925 | Kraitchik |
اعتبارا من يناير 2021[تحديث], 356 prime factors of Fermat numbers are known, and 312 Fermat numbers are known to be composite.[4] Several new Fermat factors are found each year.[8]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pseudoprimes and Fermat numbers
Like composite numbers of the form 2p − 1, every composite Fermat number is a strong pseudoprime to base 2. This is because all strong pseudoprimes to base 2 are also Fermat pseudoprimes - i.e.
for all Fermat numbers.
In 1904, Cipolla showed that the product of at least two distinct prime or composite Fermat numbers will be a Fermat pseudoprime to base 2 if and only if .[9]
مبرهنات أخرى عن أعداد فيرما
Lemma. — If n is a positive integer,
Theorem — If is an odd prime, then is a power of 2.
If is a positive integer but not a power of 2, it must have an odd prime factor , and we may write where .
By the preceding lemma, for positive integer ,
where means "evenly divides". Substituting , and and using that is odd,
and thus
Because , it follows that is not prime. Therefore, by contraposition must be a power of 2.
Theorem — A Fermat prime cannot be a Wieferich prime.
We show if is a Fermat prime (and hence by the above, m is a power of 2), then the congruence does not hold.
Since we may write . If the given congruence holds, then , and therefore
Hence , and therefore . This leads to , which is impossible since .
Theorem (Édouard Lucas) — Any prime divisor p of is of the form whenever n > 1.
Let Gp denote the group of non-zero integers modulo p under multiplication, which has order p−1. Notice that 2 (strictly speaking, its image modulo p) has multiplicative order equal to in Gp (since is the square of which is −1 modulo Fn), so that, by Lagrange's theorem, p − 1 is divisible by and p has the form for some integer k, as Euler knew. Édouard Lucas went further. Since n > 1, the prime p above is congruent to 1 modulo 8. Hence (as was known to Carl Friedrich Gauss), 2 is a quadratic residue modulo p, that is, there is integer a such that Then the image of a has order in the group Gp and (using Lagrange's theorem again), p − 1 is divisible by and p has the form for some integer s.
In fact, it can be seen directly that 2 is a quadratic residue modulo p, since
Since an odd power of 2 is a quadratic residue modulo p, so is 2 itself.
A Fermat number cannot be a perfect number or part of a pair of amicable numbers. (Luca 2000)
The series of reciprocals of all prime divisors of Fermat numbers is convergent. (Křížek, Luca & Somer 2002)
If nn + 1 is prime, there exists an integer m such that n = 22m. The equation nn + 1 = F(2m+m) holds in that case.[10][11]
Let the largest prime factor of the Fermat number Fn be P(Fn). Then,
العلاقة بالمضلعات القابلة للإنشاء
طوّر كارل فريدريش گاوس نظرية Gaussian periods in his Disquisitiones Arithmeticae and formulated a sufficient condition for the constructibility of regular polygons. Gauss stated that this condition was also necessary, but never published a proof. Pierre Wantzel gave a full proof of necessity in 1837. The result is known as the Gauss–Wantzel theorem:
- An n-sided regular polygon can be constructed with compass and straightedge if and only if n is the product of a power of 2 and distinct Fermat primes: in other words, if and only if n is of the form n = 2kp1p2...ps, where k, s are nonnegative integers and the pi are distinct Fermat primes.
A positive integer n is of the above form if and only if its totient φ(n) is a power of 2.
تطبيقات أعداد فيرما
توليد أعداد عشوائية كاذبة
Fermat primes are particularly useful in generating pseudo-random sequences of numbers in the range 1 ... N, where N is a power of 2. The most common method used is to take any seed value between 1 and P − 1, where P is a Fermat prime. Now multiply this by a number A, which is greater than the square root of P and is a primitive root modulo P (i.e., it is not a quadratic residue). Then take the result modulo P. The result is the new value for the RNG.
This is useful in computer science, since most data structures have members with 2X possible values. For example, a byte has 256 (28) possible values (0–255). Therefore, to fill a byte or bytes with random values, a random number generator that produces values 1–256 can be used, the byte taking the output value −1. Very large Fermat primes are of particular interest in data encryption for this reason. This method produces only pseudorandom values, as after P − 1 repetitions, the sequence repeats. A poorly chosen multiplier can result in the sequence repeating sooner than P − 1.
أعداد فيرما المعممة
Numbers of the form with a, b any coprime integers, a > b > 0, are called generalized Fermat numbers. An odd prime p is a generalized Fermat number if and only if p is congruent to 1 (mod 4). (Here we consider only the case n > 0, so 3 = is not a counterexample.)
An example of a probable prime of this form is 1215131072 + 242131072 (found by Kellen Shenton).[12]
By analogy with the ordinary Fermat numbers, it is common to write generalized Fermat numbers of the form as Fn(a). In this notation, for instance, the number 100,000,001 would be written as F3(10). In the following we shall restrict ourselves to primes of this form, , such primes are called "Fermat primes base a". Of course, these primes exist only if a is even.
If we require n > 0, then Landau's fourth problem asks if there are infinitely many generalized Fermat primes Fn(a).
أعداد فيرما الأولية المعممة
Because of the ease of proving their primality, generalized Fermat primes have become in recent years a topic for research within the field of number theory. Many of the largest known primes today are generalized Fermat primes.
Generalized Fermat numbers can be prime only for even a, because if a is odd then every generalized Fermat number will be divisible by 2. The smallest prime number with is , or 3032 + 1. Besides, we can define "half generalized Fermat numbers" for an odd base, a half generalized Fermat number to base a (for odd a) is , and it is also to be expected that there will be only finitely many half generalized Fermat primes for each odd base.
(In the list, the generalized Fermat numbers () to an even a are , for odd a, they are . If a is a perfect power with an odd exponent (المتتالية A070265 في OEIS), then all generalized Fermat number can be algebraic factored, so they cannot be prime)
(For the smallest number such that is prime, see قالب:Oeis)
| numbers such that is prime |
numbers such that is prime |
numbers such that is prime |
numbers such that is prime | ||||
|---|---|---|---|---|---|---|---|
| 2 | 0, 1, 2, 3, 4, ... | 18 | 0, ... | 34 | 2, ... | 50 | ... |
| 3 | 0, 1, 2, 4, 5, 6, ... | 19 | 1, ... | 35 | 1, 2, 6, ... | 51 | 1, 3, 6, ... |
| 4 | 0, 1, 2, 3, ... | 20 | 1, 2, ... | 36 | 0, 1, ... | 52 | 0, ... |
| 5 | 0, 1, 2, ... | 21 | 0, 2, 5, ... | 37 | 0, ... | 53 | 3, ... |
| 6 | 0, 1, 2, ... | 22 | 0, ... | 38 | ... | 54 | 1, 2, 5, ... |
| 7 | 2, ... | 23 | 2, ... | 39 | 1, 2, ... | 55 | ... |
| 8 | (none) | 24 | 1, 2, ... | 40 | 0, 1, ... | 56 | 1, 2, ... |
| 9 | 0, 1, 3, 4, 5, ... | 25 | 0, 1, ... | 41 | 4, ... | 57 | 0, 2, ... |
| 10 | 0, 1, ... | 26 | 1, ... | 42 | 0, ... | 58 | 0, ... |
| 11 | 1, 2, ... | 27 | (none) | 43 | 3, ... | 59 | 1, ... |
| 12 | 0, ... | 28 | 0, 2, ... | 44 | 4, ... | 60 | 0, ... |
| 13 | 0, 2, 3, ... | 29 | 1, 2, 4, ... | 45 | 0, 1, ... | 61 | 0, 1, 2, ... |
| 14 | 1, ... | 30 | 0, 5, ... | 46 | 0, 2, 9, ... | 62 | ... |
| 15 | 1, ... | 31 | ... | 47 | 3, ... | 63 | ... |
| 16 | 0, 1, 2, ... | 32 | (none) | 48 | 2, ... | 64 | (none) |
| 17 | 2, ... | 33 | 0, 3, ... | 49 | 1, ... | 65 | 1, 2, 5, ... |
| b | known generalized (half) Fermat prime base b |
| 2 | 3, 5, 17, 257, 65537 |
| 3 | 2, 5, 41, 21523361, 926510094425921, 1716841910146256242328924544641 |
| 4 | 5, 17, 257, 65537 |
| 5 | 3, 13, 313 |
| 6 | 7, 37, 1297 |
| 7 | 1201 |
| 8 | (not possible) |
| 9 | 5, 41, 21523361, 926510094425921, 1716841910146256242328924544641 |
| 10 | 11, 101 |
| 11 | 61, 7321 |
| 12 | 13 |
| 13 | 7, 14281, 407865361 |
| 14 | 197 |
| 15 | 113 |
| 16 | 17, 257, 65537 |
| 17 | 41761 |
| 18 | 19 |
| 19 | 181 |
| 20 | 401, 160001 |
| 21 | 11, 97241, 1023263388750334684164671319051311082339521 |
| 22 | 23 |
| 23 | 139921 |
| 24 | 577, 331777 |
| 25 | 13, 313 |
| 26 | 677 |
| 27 | (not possible) |
| 28 | 29, 614657 |
| 29 | 421, 353641, 125123236840173674393761 |
| 30 | 31, 185302018885184100000000000000000000000000000001 |
| 31 | |
| 32 | (not possible) |
| 33 | 17, 703204309121 |
| 34 | 1336337 |
| 35 | 613, 750313, 330616742651687834074918381127337110499579842147487712949050636668246738736343104392290115356445313 |
| 36 | 37, 1297 |
| 37 | 19 |
| 38 | |
| 39 | 761, 1156721 |
| 40 | 41, 1601 |
| 41 | 31879515457326527173216321 |
| 42 | 43 |
| 43 | 5844100138801 |
| 44 | 197352587024076973231046657 |
| 45 | 23, 1013 |
| 46 | 47, 4477457, 46512+1 (852 digits: 214787904487...289480994817) |
| 47 | 11905643330881 |
| 48 | 5308417 |
| 49 | 1201 |
| 50 |
(See [13][14] for more information (even bases up to 1000), also see [15] for odd bases)
(For the smallest prime of the form (for odd ), see also قالب:Oeis)
| numbers such that is prime | ||
|---|---|---|
| 2 | 1 | 0, 1, 2, 3, 4, ... |
| 3 | 1 | 0, 1, 2, 4, 5, 6, ... |
| 3 | 2 | 0, 1, 2, ... |
| 4 | 1 | 0, 1, 2, 3, ... |
| 4 | 3 | 0, 2, 4, ... |
| 5 | 1 | 0, 1, 2, ... |
| 5 | 2 | 0, 1, 2, ... |
| 5 | 3 | 1, 2, 3, ... |
| 5 | 4 | 1, 2, ... |
| 6 | 1 | 0, 1, 2, ... |
| 6 | 5 | 0, 1, 3, 4, ... |
| 7 | 1 | 2, ... |
| 7 | 2 | 1, 2, ... |
| 7 | 3 | 0, 1, 8, ... |
| 7 | 4 | 0, 2, ... |
| 7 | 5 | 1, 4, ... |
| 7 | 6 | 0, 2, 4, ... |
| 8 | 1 | (none) |
| 8 | 3 | 0, 1, 2, ... |
| 8 | 5 | 0, 1, 2, ... |
| 8 | 7 | 1, 4, ... |
| 9 | 1 | 0, 1, 3, 4, 5, ... |
| 9 | 2 | 0, 2, ... |
| 9 | 4 | 0, 1, ... |
| 9 | 5 | 0, 1, 2, ... |
| 9 | 7 | 2, ... |
| 9 | 8 | 0, 2, 5, ... |
| 10 | 1 | 0, 1, ... |
| 10 | 3 | 0, 1, 3, ... |
| 10 | 7 | 0, 1, 2, ... |
| 10 | 9 | 0, 1, 2, ... |
| 11 | 1 | 1, 2, ... |
| 11 | 2 | 0, 2, ... |
| 11 | 3 | 0, 3, ... |
| 11 | 4 | 1, 2, ... |
| 11 | 5 | 1, ... |
| 11 | 6 | 0, 1, 2, ... |
| 11 | 7 | 2, 4, 5, ... |
| 11 | 8 | 0, 6, ... |
| 11 | 9 | 1, 2, ... |
| 11 | 10 | 5, ... |
| 12 | 1 | 0, ... |
| 12 | 5 | 0, 4, ... |
| 12 | 7 | 0, 1, 3, ... |
| 12 | 11 | 0, ... |
| 13 | 1 | 0, 2, 3, ... |
| 13 | 2 | 1, 3, 9, ... |
| 13 | 3 | 1, 2, ... |
| 13 | 4 | 0, 2, ... |
| 13 | 5 | 1, 2, 4, ... |
| 13 | 6 | 0, 6, ... |
| 13 | 7 | 1, ... |
| 13 | 8 | 1, 3, 4, ... |
| 13 | 9 | 0, 3, ... |
| 13 | 10 | 0, 1, 2, 4, ... |
| 13 | 11 | 2, ... |
| 13 | 12 | 1, 2, 5, ... |
| 14 | 1 | 1, ... |
| 14 | 3 | 0, 3, ... |
| 14 | 5 | 0, 2, 4, 8, ... |
| 14 | 9 | 0, 1, 8, ... |
| 14 | 11 | 1, ... |
| 14 | 13 | 2, ... |
| 15 | 1 | 1, ... |
| 15 | 2 | 0, 1, ... |
| 15 | 4 | 0, 1, ... |
| 15 | 7 | 0, 1, 2, ... |
| 15 | 8 | 0, 2, 3, ... |
| 15 | 11 | 0, 1, 2, ... |
| 15 | 13 | 1, 4, ... |
| 15 | 14 | 0, 1, 2, 4, ... |
| 16 | 1 | 0, 1, 2, ... |
| 16 | 3 | 0, 2, 8, ... |
| 16 | 5 | 1, 2, ... |
| 16 | 7 | 0, 6, ... |
| 16 | 9 | 1, 3, ... |
| 16 | 11 | 2, 4, ... |
| 16 | 13 | 0, 3, ... |
| 16 | 15 | 0, ... |
(For the smallest even base a such that is prime, see قالب:Oeis)
| bases a such that is prime (only consider even a) | OEIS sequence | |
|---|---|---|
| 0 | 2, 4, 6, 10, 12, 16, 18, 22, 28, 30, 36, 40, 42, 46, 52, 58, 60, 66, 70, 72, 78, 82, 88, 96, 100, 102, 106, 108, 112, 126, 130, 136, 138, 148, 150, ... | قالب:OEIS link |
| 1 | 2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56, 66, 74, 84, 90, 94, 110, 116, 120, 124, 126, 130, 134, 146, 150, 156, 160, 170, 176, 180, 184, ... | قالب:OEIS link |
| 2 | 2, 4, 6, 16, 20, 24, 28, 34, 46, 48, 54, 56, 74, 80, 82, 88, 90, 106, 118, 132, 140, 142, 154, 160, 164, 174, 180, 194, 198, 204, 210, 220, 228, ... | قالب:OEIS link |
| 3 | 2, 4, 118, 132, 140, 152, 208, 240, 242, 288, 290, 306, 378, 392, 426, 434, 442, 508, 510, 540, 542, 562, 596, 610, 664, 680, 682, 732, 782, ... | قالب:OEIS link |
| 4 | 2, 44, 74, 76, 94, 156, 158, 176, 188, 198, 248, 288, 306, 318, 330, 348, 370, 382, 396, 452, 456, 470, 474, 476, 478, 560, 568, 598, 642, ... | قالب:OEIS link |
| 5 | 30, 54, 96, 112, 114, 132, 156, 332, 342, 360, 376, 428, 430, 432, 448, 562, 588, 726, 738, 804, 850, 884, 1068, 1142, 1198, 1306, 1540, 1568, ... | قالب:OEIS link |
| 6 | 102, 162, 274, 300, 412, 562, 592, 728, 1084, 1094, 1108, 1120, 1200, 1558, 1566, 1630, 1804, 1876, 2094, 2162, 2164, 2238, 2336, 2388, ... | قالب:OEIS link |
| 7 | 120, 190, 234, 506, 532, 548, 960, 1738, 1786, 2884, 3000, 3420, 3476, 3658, 4258, 5788, 6080, 6562, 6750, 7692, 8296, 9108, 9356, 9582, ... | قالب:OEIS link |
| 8 | 278, 614, 892, 898, 1348, 1494, 1574, 1938, 2116, 2122, 2278, 2762, 3434, 4094, 4204, 4728, 5712, 5744, 6066, 6508, 6930, 7022, 7332, ... | قالب:OEIS link |
| 9 | 46, 1036, 1318, 1342, 2472, 2926, 3154, 3878, 4386, 4464, 4474, 4482, 4616, 4688, 5374, 5698, 5716, 5770, 6268, 6386, 6682, 7388, 7992, ... | قالب:OEIS link |
| 10 | 824, 1476, 1632, 2462, 2484, 2520, 3064, 3402, 3820, 4026, 6640, 7026, 7158, 9070, 12202, 12548, 12994, 13042, 15358, 17646, 17670, ... | قالب:OEIS link |
| 11 | 150, 2558, 4650, 4772, 11272, 13236, 15048, 23302, 26946, 29504, 31614, 33308, 35054, 36702, 37062, 39020, 39056, 43738, 44174, 45654, ... | قالب:OEIS link |
| 12 | 1534, 7316, 17582, 18224, 28234, 34954, 41336, 48824, 51558, 51914, 57394, 61686, 62060, 89762, 96632, 98242, 100540, 101578, 109696, ... | قالب:OEIS link |
| 13 | 30406, 71852, 85654, 111850, 126308, 134492, 144642, 147942, 150152, 165894, 176206, 180924, 201170, 212724, 222764, 225174, 241600, ... | قالب:OEIS link |
| 14 | 67234, 101830, 114024, 133858, 162192, 165306, 210714, 216968, 229310, 232798, 422666, 426690, 449732, 462470, 468144, 498904, 506664, ... | قالب:OEIS link |
| 15 | 70906, 167176, 204462, 249830, 321164, 330716, 332554, 429370, 499310, 524552, 553602, 743788, 825324, 831648, 855124, 999236, 1041870, ... | قالب:OEIS link |
| 16 | 48594, 108368, 141146, 189590, 255694, 291726, 292550, 357868, 440846, 544118, 549868, 671600, 843832, 857678, 1024390, 1057476, 1087540, ... | قالب:OEIS link |
| 17 | 62722, 130816, 228188, 386892, 572186, 689186, 909548, 1063730, 1176694, 1361244, 1372930, 1560730, 1660830, 1717162, 1722230, 1766192, ... | قالب:OEIS link |
| 18 | 24518, 40734, 145310, 361658, 525094, 676754, 773620, 1415198, 1488256, 1615588, 1828858, 2042774, 2514168, 2611294, 2676404, 3060772, ... | قالب:OEIS link |
| 19 | 75898, 341112, 356926, 475856, 1880370, 2061748, 2312092, 2733014, 2788032, 2877652, 2985036, 3214654, 3638450, 4896418, ... | قالب:OEIS link |
| 20 | 919444, 1059094, 1951734, 1963736, ... | قالب:OEIS link |
The smallest base b such that b2n + 1 is prime are
- 2, 2, 2, 2, 2, 30, 102, 120, 278, 46, 824, 150, 1534, 30406, 67234, 70906, 48594, 62722, 24518, 75898, 919444, ... (المتتالية A056993 في OEIS)
The smallest k such that (2n)k + 1 is prime are
- 1, 1, 1, 0, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 0, 4, 1, ... (The next term is unknown) (المتتالية A079706 في OEIS) (also see قالب:Oeis and قالب:Oeis)
A more elaborate theory can be used to predict the number of bases for which will be prime for fixed . The number of generalized Fermat primes can be roughly expected to halve as is increased by 1.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
أكبر أعداد فيرما الأولية المعممة المعروفة
The following is a list of the 5 largest known generalized Fermat primes.[16] The whole top-5 is discovered by participants in the PrimeGrid project.
| الرتبة | العدد الأولي | ترميز فيرما المعمم | عدد الأرقام | تاريخ الاكتشاف | ref. |
|---|---|---|---|---|---|
| 1 | 19637361048576 + 1 | F20(1963736) | 6,598,776 | Sep 2022 | [17] |
| 2 | 19517341048576 + 1 | F20(1951734) | 6,595,985 | Aug 2022 | [18] |
| 3 | 10590941048576 + 1 | F20(1059094) | 6,317,602 | Nov 2018 | [19] |
| 4 | 9194441048576 + 1 | F20(919444) | 6,253,210 | Sep 2017 | [20] |
| 5 | 25×213719266 + 1 | F1(5×26859633) | 4,129,912 | Sep 2022 | [21] |
On the Prime Pages one can find the current top 100 generalized Fermat primes.
انظر أيضاً
- مضلع قابل للإنشاء: which regular polygons are constructible partially depends on Fermat primes.
- Double exponential function
- مبرهنة لوكاس
- عدد مرسن الأولي
- Pierpont prime
- Primality test
- Proth's theorem
- عدد أولي زائف
- Sierpiński number
- Sylvester's sequence
الهامش
- ^ Křížek, Luca & Somer 2001, p. 38, Remark 4.15
- ^ Chris Caldwell, "Prime Links++: special forms" Archived 2013-12-24 at the Wayback Machine at The Prime Pages.
- ^ Ribenboim 1996, p. 88.
- ^ أ ب ت Keller, Wilfrid (January 18, 2021), Prime Factors of Fermat Numbers, http://www.prothsearch.com/fermat.html#Summary, retrieved on January 19, 2021
- ^ Boklan, Kent D.; Conway, John H. (2017). "Expect at most one billionth of a new Fermat Prime!". The Mathematical Intelligencer. 39 (1): 3–5. arXiv:1605.01371. doi:10.1007/s00283-016-9644-3. S2CID 119165671.
- ^ Sandifer, Ed. "How Euler Did it" (PDF). MAA Online. Mathematical Association of America. Archived (PDF) from the original on 2022-10-09. Retrieved 2020-06-13.
- ^ ":: F E R M A T S E A R C H . O R G :: Home page". www.fermatsearch.org. Retrieved 7 April 2018.
- ^ ":: F E R M A T S E A R C H . O R G :: News". www.fermatsearch.org. Retrieved 7 April 2018.
- ^ Krizek, Michal; Luca, Florian; Somer, Lawrence (14 March 2013). 17 Lectures on Fermat Numbers: From Number Theory to Geometry. Springer Science & Business Media. ISBN 9780387218502. Retrieved 7 April 2018 – via Google Books.
- ^ Jeppe Stig Nielsen, "S(n) = n^n + 1".
- ^ Eric W. Weisstein, Sierpiński Number of the First Kind at MathWorld.
- ^ PRP Top Records, search for x^131072+y^131072, by Henri & Renaud Lifchitz.
- ^ "Generalized Fermat Primes". jeppesn.dk. Retrieved 7 April 2018.
- ^ "Generalized Fermat primes for bases up to 1030". noprimeleftbehind.net. Retrieved 7 April 2018.
- ^ "Generalized Fermat primes in odd bases". fermatquotient.com. Retrieved 7 April 2018.
- ^ Caldwell, Chris K. "The Top Twenty: Generalized Fermat". The Prime Pages. Retrieved 11 July 2019.
- ^ 19637361048576 + 1
- ^ 19517341048576 + 1
- ^ 10590941048576 + 1
- ^ 9194441048576 + 1
- ^ 25*213719266 + 1
مراجع
- 17 Lectures on Fermat Numbers: From Number Theory to Geometry, Michal Křížek, Florian Luca, Lawrence Somer, Springer, CMS Books 9, ISBN 0-387-95332-9 (This book contains an extensive list of references.)
- S. W. Golomb, On the sum of the reciprocals of the Fermat numbers and related irrationalities, Canad. J. Math. 15(1963), 475--478.
- Richard K. Guy, Unsolved Problems in Number Theory (3rd ed), Springer Verlag, 2004 ISBN 0-387-20860-7; sections A3,A12,B21.
- Florian Luca, The anti-social Fermat number, Amer. Math. Monthly 107(2000), 171--173.
- Michal Krizek, Florian Luca and Lawrence Somer(2002), On the convergence of series of reciprocals of primes related to the Fermat numbers, J. Number Theory 97(2002), 95--112.
- A. Grytczuk, F. Luca and M. Wojtowicz(2001), Another note on the greatest prime factors of Fermat numbers, Southeast Asian Bull. Math. 25(2001), 111--115.
وصلات خارجية
- Chris Caldwell, The Prime Glossary: Fermat number at The Prime Pages.
- Luigi Morelli, History of Fermat Numbers
- John Cosgrave, Unification of Mersenne and Fermat Numbers
- Wilfrid Keller, Prime Factors of Fermat Numbers
- Eric W. Weisstein, Fermat Number at MathWorld.
- Eric W. Weisstein, Fermat Prime at MathWorld.
- Eric W. Weisstein, Generalized Fermat Number at MathWorld.
- Yves Gallot, Generalized Fermat Prime Search
- Mark S. Manasse, Complete factorization of the ninth Fermat number (original announcement)
- Peyton Hayslette, Largest Known Generalized Fermat Prime Announcement
- Short description matches Wikidata
- مقالات فيها عبارات متقادمة منذ 2014
- جميع المقالات التي فيها عبارات متقادمة
- مقالات فيها عبارات متقادمة منذ نوفمبر 2021
- مقالات فيها عبارات متقادمة منذ يناير 2021
- Harv and Sfn no-target errors
- Constructible polygons
- Articles containing proofs
- Unsolved problems in number theory
- Large integers
- Classes of prime numbers
- متتاليات أعداد صحيحة
- نظرية الأعداد
- هندسة إقليدية مستوية
- أعداد كبيرة