عدد ممركز مسدسي

Centered hexagonal numbers appearing in the Catan board game:
19 land tiles,
37 total tiles

عدد ممركز مسدسي Centered hexagonal number‏^[1]^[2] هو عدد ممركز مضلع يمثل شكل مسدس (هندسة) له نقطة مركزية والنقاط الأخرى تتوزع على طبقات حولها مشكلة شكل مضلع مسدس الأضلاع. The following figures illustrate this arrangement for the first four centered hexagonal numbers:

1		7		19		37
+1		+6		+12		+18

Centered hexagonal numbers should not be confused with cornered hexagonal numbers, which are figurate numbers in which the associated hexagons share a vertex.

The sequence of hexagonal numbers starts out as follows (المتتالية A003215 في OEIS):

1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Formula

Dissection of hexagonal number into six triangles with a remainder of one. The triangles can be re-assembled pairwise to give three parallelograms of

n (n -1)

dots each.

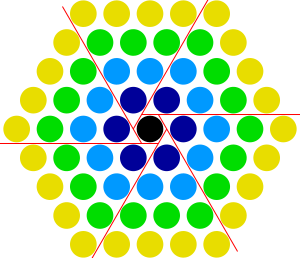
The $n$ th centered hexagonal number is given by the formula^[2]

H(n)=n^{3}-(n-1)^{3}=3n(n-1)+1=3n^{2}-3n+1.\,

Expressing the formula as

H(n)=1+6\left({\frac {n(n-1)}{2}}\right)

shows that the centered hexagonal number for $n$ is 1 more than 6 times the $(n - 1)$ th triangular number.

In the opposite direction, the index $n$ corresponding to the centered hexagonal number $H=H(n)$ can be calculated using the formula

n={\frac {3+{\sqrt {12H-3}}}{6}}.

This can be used as a test for whether a number $H$ is centered hexagonal: it will be if and only if the above expression is an integer.

Recurrence and generating function

The centered hexagonal numbers $H(n)$ satisfy the recurrence relation^[2]

H(n+1)=H(n)+6n.

From this we can calculate the generating function $F(x)=\sum _{n\geq 0}H(x)x^{n}$ . The generating function satisfies

F(x)=x+xF(x)+\sum _{n\geq 2}6nx^{n}.

The latter term is the Taylor series of ${\frac {6x}{(1-x)^{2}}}-6x$ , so we get

(1-x)F(x)=x+{\frac {6x}{(1-x)^{2}}}-6x={\frac {x+4x^{2}+x^{3}}{(1-x)^{2}}}

and end up at

F(x)={\frac {x+4x^{2}+x^{3}}{(1-x)^{3}}}.

Properties

In base 10 one can notice that the hexagonal numbers' rightmost (least significant) digits follow the pattern 1–7–9–7–1 (repeating with period 5). This follows from the last digit of the triangle numbers (المتتالية A008954 في OEIS) which repeat 0-1-3-1-0 when taken modulo 5. In base 6 the rightmost digit is always 1: 1₆, 11₆, 31₆, 101₆, 141₆, 231₆, 331₆, 441₆... This follows from the fact that every centered hexagonal number modulo 6 (=10₆) equals 1.

The sum of the first $n$ centered hexagonal numbers is $n 3$ . That is, centered hexagonal pyramidal numbers and cubes are the same numbers, but they represent different shapes. Viewed from the opposite perspective, centered hexagonal numbers are differences of two consecutive cubes, so that the centered hexagonal numbers are the gnomon of the cubes. (This can be seen geometrically from the diagram.) In particular, prime centered hexagonal numbers are cuban primes.

The difference between $(2 n) 2$ and the $n$ th centered hexagonal number is a number of the form $3 n 2 + 3 n - 1$ , while the difference between $(2 n - 1) 2$ and the $n$ th centered hexagonal number is a pronic number.

Applications

Ignoring central holes, the number of mirror segments in several segmented mirror telescopes are centered hexagonal numbers

Many segmented mirror reflecting telescopes have primary mirrors comprising a centered hexagonal number of segments (neglecting the central segment removed to allow passage of light) to simplify the control system.^[3] Some examples:

Telescope	Number of segments	Number missing	Total	n-th centered hexagonal number
Giant Magellan Telescope	7	0	7	2
James Webb Space Telescope	18	1	19	3
Gran Telescopio Canarias	36	1	37	4
Guido Horn d'Arturo's prototype	61	0	61	5
Southern African Large Telescope	91	0	91	6

References

^ Hindin, H. J. (1983). "Stars, hexes, triangular numbers and Pythagorean triples". J. Rec. Math. 16: 191–193.
^ ^أ ^ب ^ت Deza, Elena; Deza, M. (2012). Figurate Numbers (in الإنجليزية). World Scientific. pp. 47–55. ISBN 978-981-4355-48-3.
^ Mast, T S, and Nelson, J E. Figure control for a segmented telescope mirror. United States: N. p., 1979. Web. doi:10.2172/6194407.

Formula

Recurrence and generating function

Properties

Applications

References

See also