جذر تربيعي

في الرياضيات، الجذر التربيعي لرقم (X) هو الرقم (Y) الذي إذا ضرب في نفسه ينتج الرقم (X) . مثال:

${\sqrt {9}}=3$, $3^{2}=3\times 3=9$.

الجذر التربيعي للعدد المربع الكامل. 5×5 = 25 = 25. نقول: 5×5 هي عملية تربيع للعدد 5

لا يوجد جذر تربيعي للأعداد السالبة ضمن مجموعة الأعداد الحقيقية.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الخصائص

مخطط تابع الجذر التربيعي f(x) = √x,حيث يأخذ شكل نصف قطع مكافئ.

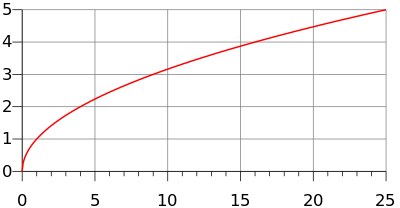
• تابع الجذر التربيعي ذو الشكل f(x) = √x هو تابع يربط مجموعة الأعداد الحقيقية الموجبة R⁺ ∪ 0 بنفسها، ومثله مثل جميع التوابع الأخرى فإنه ينتج دائماً قيمة فريدة.

• في مصطلحات الهندسة الرياضية فإن الجذر التربيعي لمساحة مربع يعطي طول ضلع هذا المربع.

• من أجل جميع أي عدد حقيقي x

${\sqrt {x^{2}}}=\left|x\right|={\begin{cases}x,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x\leq 0\end{cases}}$

• من أجل أي عددين حقيقين موجبين x ، y يتحقق

${\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}$

and

${\sqrt {x}}=x^{\frac {1}{2}}.$

• يعطى مشتق تابع الجذر التربيعي بالعلاقة:

$f'(x)={\frac {1}{2{\sqrt {x}}}}.$

• تعطى سلسلة تايلور للحد √1 + x حول x = 0 بالعلاقة:

${\sqrt {1+x}}=1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots \!$

 جذور الأعداد الطبيعية

الأرقام التي لها جذر تربيعي في مجموعة الأعداد الصحيحة بالتسلسل:

• 1=1 أول رقم له جذر تربيعي
• 1 + 3 = 4 ثاني رقم له جذر تربيعي
• 1 + 3 + 5 = 9 ثالث رقم له جذر تربيعي
• 1 + 3 + 5 + 7 = 16 رابع رقم له جذر تربيعي
• 1 + 3 + 5 + 7 + 9 = 25 خامس رقم له جذر تربيعي
• 1 + 3 + 5 + 7 + 9 + 11 = 36 سادس رقم له جذر تربيعي
• 1 + 3 + 5 + 7 + 9 + 11 + 13 =49 سابع عدد له جذر تربيعي
• و هكذا بالتسلسل

 جبر

• أس