الميكانيكا المدارية

A satellite orbiting the earth has a tangential velocity and an inward acceleration.

الميكانيكا المدارية Orbital mechanics أو الديناميكا الفلكية Dynamics of astronomical هى فرع من علم الديناميكا ( حركة الاجسام) يختص بدراسة حركات الاقمار الصناعية والسوابر الفضائية كسوابر الدفع والمجالا المتعلقة بتخطي وتوجيه مسارات تلك الاقمار والسوابر.

Celestial mechanics treats more broadly the orbital dynamics of systems under the influence of gravity, including both spacecraft and natural astronomical bodies such as star systems, planets, moons, and comets. Orbital mechanics focuses on spacecraft trajectories, including orbital maneuvers, orbital plane changes, and interplanetary transfers, and is used by mission planners to predict the results of propulsive maneuvers.

General relativity is a more exact theory than Newton's laws for calculating orbits, and it is sometimes necessary to use it for greater accuracy or in high-gravity situations (e.g. orbits near the Sun).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التاريخ

Until the rise of space travel in the twentieth century, there was little distinction between orbital and celestial mechanics. At the time of Sputnik, the field was termed 'space dynamics'. The fundamental techniques, such as those used to solve the Keplerian problem (determining position as a function of time), are therefore the same in both fields. Furthermore, the history of the fields is almost entirely shared.

Johannes Kepler was the first to successfully model planetary orbits to a high degree of accuracy, publishing his laws in 1605. Isaac Newton published more general laws of celestial motion in the first edition of Philosophiæ Naturalis Principia Mathematica (1687), which gave a method for finding the orbit of a body following a parabolic path from three observations. This was used by Edmund Halley to establish the orbits of various comets, including that which bears his name. Newton's method of successive approximation was formalised into an analytic method by Leonhard Euler in 1744, whose work was in turn generalised to elliptical and hyperbolic orbits by Johann Lambert in 1761–1777.

Another milestone in orbit determination was Carl Friedrich Gauss's assistance in the "recovery" of the dwarf planet Ceres in 1801. Gauss's method was able to use just three observations (in the form of pairs of right ascension and declination), to find the six orbital elements that completely describe an orbit. The theory of orbit determination has subsequently been developed to the point where today it is applied in GPS receivers as well as the tracking and cataloguing of newly observed minor planets. Modern orbit determination and prediction are used to operate all types of satellites and space probes, as it is necessary to know their future positions to a high degree of accuracy.

Astrodynamics was developed by astronomer Samuel Herrick beginning in the 1930s. He consulted the rocket scientist Robert Goddard and was encouraged to continue his work on space navigation techniques, as Goddard believed they would be needed in the future. Numerical techniques of astrodynamics were coupled with new powerful computers in the 1960s, and humans were ready to travel to the Moon and return.

 التقنيات العملية

للمزيد من المعلومات: List of orbits

 قواعد الإبهام

The following rules of thumb are useful for situations approximated by classical mechanics under the standard assumptions of astrodynamics outlined below. The specific example discussed is of a satellite orbiting a planet, but the rules of thumb could also apply to other situations, such as orbits of small bodies around a star such as the Sun.

• Kepler's laws of planetary motion:

 حساب المسارات

 معادلة كپلر

One approach to calculating orbits (mainly used historically) is to use Kepler's equation:

$M=E-\epsilon \cdot \sin E$.

where M is the mean anomaly, E is the eccentric anomaly, and $\epsilon$ is the eccentricity.

With Kepler's formula, finding the time-of-flight to reach an angle (true anomaly) of $\theta$ from periapsis is broken into two steps:

1. Compute the eccentric anomaly $E$ from true anomaly $\theta$
2. Compute the time-of-flight $t$ from the eccentric anomaly $E$

Finding the eccentric anomaly at a given time (the inverse problem) is more difficult. Kepler's equation is transcendental in $E$, meaning it cannot be solved for $E$ algebraically. Kepler's equation can be solved for $E$ analytically by inversion.

A solution of Kepler's equation, valid for all real values of $\textstyle \epsilon$ is:

$$E={\begin{cases}\displaystyle \sum _{n=1}^{\infty }{\frac {M^{\frac {n}{3}}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left[\left({\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}\right)^{n}\right]\right),&\epsilon =1\\\displaystyle \sum _{n=1}^{\infty }{\frac {M^{n}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left[\left({\frac {\theta }{\theta -\epsilon \cdot \sin(\theta )}}\right)^{n}\right]\right),&\epsilon \neq 1\end{cases}}$$

Evaluating this yields:

$$E={\begin{cases}\displaystyle x+{\frac {1}{60}}x^{3}+{\frac {1}{1400}}x^{5}+{\frac {1}{25200}}x^{7}+{\frac {43}{17248000}}x^{9}+{\frac {1213}{7207200000}}x^{11}+{\frac {151439}{12713500800000}}x^{13}\cdots \ |\ x=(6M)^{\frac {1}{3}},&\epsilon =1\\\\\displaystyle {\frac {1}{1-\epsilon }}M-{\frac {\epsilon }{(1-\epsilon )^{4}}}{\frac {M^{3}}{3!}}+{\frac {(9\epsilon ^{2}+\epsilon )}{(1-\epsilon )^{7}}}{\frac {M^{5}}{5!}}-{\frac {(225\epsilon ^{3}+54\epsilon ^{2}+\epsilon )}{(1-\epsilon )^{10}}}{\frac {M^{7}}{7!}}+{\frac {(11025\epsilon ^{4}+4131\epsilon ^{3}+243\epsilon ^{2}+\epsilon )}{(1-\epsilon )^{13}}}{\frac {M^{9}}{9!}}\cdots ,&\epsilon \neq 1\end{cases}}$$

Alternatively, Kepler's Equation can be solved numerically. First one must guess a value of $E$ and solve for time-of-flight; then adjust $E$ as necessary to bring the computed time-of-flight closer to the desired value until the required precision is achieved. Usually, Newton's method is used to achieve relatively fast convergence.

The main difficulty with this approach is that it can take prohibitively long to converge for the extreme elliptical orbits. For near-parabolic orbits, eccentricity $\epsilon$ is nearly 1, and substituting $e=1$ into the formula for mean anomaly, $E-\sin E$, we find ourselves subtracting two nearly-equal values, and accuracy suffers. For near-circular orbits, it is hard to find the periapsis in the first place (and truly circular orbits have no periapsis at all). Furthermore, the equation was derived on the assumption of an elliptical orbit, and so it does not hold for parabolic or hyperbolic orbits. These difficulties are what led to the development of the universal variable formulation, described below.

 Conic orbits

For simple procedures, such as computing the delta-v for coplanar transfer ellipses, traditional approaches are fairly effective. Others, such as time-of-flight are far more complicated, especially for near-circular and hyperbolic orbits.

 The patched conic approximation

المقالة الرئيسية: Patched conic approximation

The size of the "neighborhoods" (or spheres of influence) vary with radius $r_{SOI}$:

$r_{SOI}=a_{p}\left({\frac {m_{p}}{m_{s}}}\right)^{2/5}$

where $a_{p}$ is the semimajor axis of the planet's orbit relative to the Sun; $m_{p}$ and $m_{s}$ are the masses of the planet and Sun, respectively.

This simplification is sufficient to compute rough estimates of fuel requirements, and rough time-of-flight estimates, but it is not generally accurate enough to guide a spacecraft to its destination. For that, numerical methods are required.

 The universal variable formulation

To address computational shortcomings of traditional approaches for solving the 2-body problem, the universal variable formulation was developed. It works equally well for the circular, elliptical, parabolic, and hyperbolic cases, the differential equations converging well when integrated for any orbit. It also generalizes well to problems incorporating perturbation theory.

 Perturbations

The universal variable formulation works well with the variation of parameters technique, except now, instead of the six Keplerian orbital elements, we use a different set of orbital elements: namely, the satellite's initial position and velocity vectors $x_{0}$ and $v_{0}$ at a given epoch $t=0$. In a two-body simulation, these elements are sufficient to compute the satellite's position and velocity at any time in the future, using the universal variable formulation. Conversely, at any moment in the satellite's orbit, we can measure its position and velocity, and then use the universal variable approach to determine what its initial position and velocity would have been at the epoch. In perfect two-body motion, these orbital elements would be invariant (just like the Keplerian elements would be).

However, perturbations cause the orbital elements to change over time. Hence, we write the position element as $x_{0}(t)$ and the velocity element as $v_{0}(t)$, indicating that they vary with time. The technique to compute the effect of perturbations becomes one of finding expressions, either exact or approximate, for the functions $x_{0}(t)$ and $v_{0}(t)$.

The following are some effects which make real orbits differ from the simple models based on a spherical earth. Most of them can be handled on short timescales (perhaps less than a few thousand orbits) by perturbation theory because they are small relative to the corresponding two-body effects.

• Equatorial bulges cause precession of the node and the perigee
• Tesseral harmonics of the gravity field introduce additional perturbations
• Lunar and solar gravity perturbations alter the orbits
• Atmospheric drag reduces the semi-major axis unless make-up thrust is used

Over very long timescales (perhaps millions of orbits), even small perturbations can dominate, and the behavior can become chaotic. On the other hand, the various perturbations can be orchestrated by clever astrodynamicists to assist with orbit maintenance tasks, such as station-keeping, ground track maintenance or adjustment, or phasing of perigee to cover selected targets at low altitude.

 Orbital maneuver

المقالة الرئيسية: Orbital maneuver

In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft. For spacecraft far from Earth—for example those in orbits around the Sun—an orbital maneuver is called a deep-space maneuver (DSM).قالب:Citation needed lead

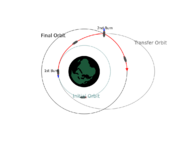
 الانتقال المداري

Transfer orbits are usually elliptical orbits that allow spacecraft to move from one (usually substantially circular) orbit to another. Usually they require a burn at the start, a burn at the end, and sometimes one or more burns in the middle.

• The Hohmann transfer orbit requires a minimal delta-v.
• A bi-elliptic transfer can require less energy than the Hohmann transfer, if the ratio of orbits is 11.94 or greater, but comes at the cost of increased trip time over the Hohmann transfer.
• Faster transfers may use any orbit that intersects both the original and destination orbits, at the cost of higher delta-v.
• Using low thrust engines (such as electrical propulsion), if the initial orbit is supersynchronous to the final desired circular orbit then the optimal transfer orbit is achieved by thrusting continuously in the direction of the velocity at apogee. This method however takes much longer due to the low thrust.

For the case of orbital transfer between non-coplanar orbits, the change-of-plane thrust must be made at the point where the orbital planes intersect (the "node"). As the objective is to change the direction of the velocity vector by an angle equal to the angle between the planes, almost all of this thrust should be made when the spacecraft is at the node near the apoapse, when the magnitude of the velocity vector is at its lowest. However, a small fraction of the orbital inclination change can be made at the node near the periapse, by slightly angling the transfer orbit injection thrust in the direction of the desired inclination change. This works because the cosine of a small angle is very nearly one, resulting in the small plane change being effectively "free" despite the high velocity of the spacecraft near periapse, as the Oberth Effect due to the increased, slightly angled thrust exceeds the cost of the thrust in the orbit-normal axis.

A Hohmann transfer from a low circular orbit to a higher circular orbit

A bi-elliptic transfer from a low circular starting orbit (dark blue), to a higher circular orbit (red)

Generic two-impulse elliptical transfer between two circular orbits

A general transfer from a low circular orbit to a higher circular orbit

An optimal sequence for transferring a satellite from a supersynchronous to a geosynchronous orbit using electric propulsion

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

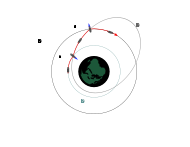
 Gravity assist and the Oberth effect

In a gravity assist, a spacecraft swings by a planet and leaves in a different direction, at a different speed. This is useful to speed or slow a spacecraft instead of carrying more fuel.

This maneuver can be approximated by an elastic collision at large distances, though the flyby does not involve any physical contact. Due to Newton's Third Law (equal and opposite reaction), any momentum gained by a spacecraft must be lost by the planet, or vice versa. However, because the planet is much, much more massive than the spacecraft, the effect on the planet's orbit is negligible.

The Oberth effect can be employed, particularly during a gravity assist operation. This effect is that use of a propulsion system works better at high speeds, and hence course changes are best done when close to a gravitating body; this can multiply the effective delta-v.

 Interplanetary Transport Network and fuzzy orbits

المقالة الرئيسية: Interplanetary Transport Network

انظر أيضاً: Low energy transfers

It is now possible to use computers to search for routes using the nonlinearities in the gravity of the planets and moons of the Solar System. For example, it is possible to plot an orbit from high earth orbit to Mars, passing close to one of the Earth's Trojan points. Collectively referred to as the Interplanetary Transport Network, these highly perturbative, even chaotic, orbital trajectories in principle need no fuel beyond that needed to reach the Lagrange point (in practice keeping to the trajectory requires some course corrections). The biggest problem with them is they can be exceedingly slow, taking many years. In addition launch windows can be very far apart.

They have, however, been employed on projects such as Genesis. This spacecraft visited the Earth-Sun ل₁ point and returned using very little propellant.

 انظر أيضاً

• Aerodynamics
• Aerospace engineering
• Astrophysics
• Canonical units
• Celestial mechanics
• Chaos theory
• Kepler orbit
• Lagrange point
• Mechanical engineering
• N-body problem
• Orbit
• Orders of magnitude (speed)
• Roche limit
• Spacecraft propulsion
• Tsiolkovsky rocket equation
• Universal variable formulation

 المراجع

• قاموس دار العلم الفلكي

• Curtis, Howard D. (2009). Orbital Mechanics for Engineering Students, 2e. New York: Elsevier. ISBN 978-0-12-374778-5.
• Bate, Roger R.; Mueller, Donald D.; White, Jerry E. (1971). Fundamentals of Astrodynamics. New York: Dover Publications. ISBN 0-486-60061-0.

• Sellers, Jerry J.; Astore, William J.; Giffen, Robert B.; Larson, Wiley J. (2004). Kirkpatrick, Douglas H. (ed.). Understanding Space: An Introduction to Astronautics (2 ed.). McGraw Hill. p. 228. ISBN 0-07-242468-0.

• "Air University Space Primer, Chapter 8 - Orbital Mechanics" (PDF). USAF. Archived from the original (PDF) on 2013-02-14. Retrieved 2007-10-13.

 للاستزادة

Many of the options, procedures, and supporting theory are covered in standard works such as:

• Bate, R.R.; Mueller, D.D.; White, J.E. (1971). Fundamentals of Astrodynamics. Dover Publications, New York. ISBN 978-0-486-60061-1.
• Vallado, D. A. (2001). Fundamentals of Astrodynamics and Applications (2nd ed.). Springer. ISBN 978-0-7923-6903-5.
• Battin, R.H. (1999). An Introduction to the Mathematics and Methods of Astrodynamics. American Institute of Aeronautics & Ast, Washington, D.C. ISBN 978-1-56347-342-5.
• Chobotov, V.A., ed. (2002). Orbital Mechanics (3rd ed.). American Institute of Aeronautics & Ast, Washington, D.C. ISBN 978-1-56347-537-5.
• Herrick, S. (1971). Astrodynamics: Orbit Determination, Space Navigation, Celestial Mechanics, Volume 1. Van Nostrand Reinhold, London. ISBN 978-0-442-03370-5.
• Herrick, S. (1972). Astrodynamics: Orbit Correction, Perturbation Theory, Integration, Volume 2. Van Nostrand Reinhold, London. ISBN 978-0-442-03371-2.
• Kaplan, M.H. (1976). Modern Spacecraft Dynamics and Controls. Wiley, New York. ISBN 978-0-471-45703-9.
• Tom Logsdon (1997). Orbital Mechanics. Wiley-Interscience, New York. ISBN 978-0-471-14636-0.
• John E. Prussing & Bruce A. Conway (1993). Orbital Mechanics. Oxford University Press, New York. ISBN 978-0-19-507834-3.
• M.J. Sidi (2000). Spacecraft Dynamics and Control. Cambridge University Press, New York. ISBN 978-0-521-78780-2.
• W.E. Wiesel (1996). Spaceflight Dynamics (2nd ed.). McGraw-Hill, New York. ISBN 978-0-07-070110-6.
• J.P. Vinti (1998). Orbital and Celestial Mechanics. American Institute of Aeronautics & Ast, Reston, Virginia. ISBN 978-1-56347-256-5.
• P. Gurfil (2006). Modern Astrodynamics. Butterworth-Heinemann. ISBN 978-0-12-373562-1.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

• ORBITAL MECHANICS (Rocket and Space Technology)
• Java Astrodynamics Toolkit
• Astrodynamics-based Space Traffic and Event Knowledge Graph