قسيم
ساهم بشكل رئيسي في تحرير هذا المقال
|
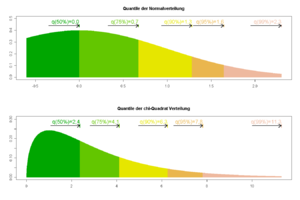
القـُسـَيـِّمات Quantile هي نقاط تؤخذ على فترات منتظمة من دالة التوزيع التراكمية لمتغير عشوائي.
قسيمات متخصصة
بعض القسيمات لها أسماء خاصة:
- ذو القسيمَيْن يسمى وسيط median
- ذو الثلاثة قسيمات يسمى ثـُلَيـِّث tertiles أو terciles → T
- الأربع قسيمات تسمى رُبـَيـِّعات quartiles → Q
- الخمس قسيمات تسمى خـُمـَيـِّسات quintile → QU
- التسع قسيمات تسمى تُسَيعات (شائع في الاختبارات التعليمية) noniles → NO
- العشرة قسيمات تسمى عُشريات deciles → D
- الاثناعشر قسيماً تسمى الاثناعشريات duo-deciles → Dd
- العشرين قسيم عشرينيات vigintiles → V
- المئة قسيم تسمى ميئينات percentiles → P
- الألف قسيم تسمى permillages → Pr
وعموماً، يمكن للمرء أن يعتبر دالة القسيم لأي توزيع. وهي معرَّفة لمتغيرات حقيقية بين صفر وواحد ورياضياً هي مقلوب دالة التوزيع التراكمية.
الطريقة العامة لإيجاد القسيمات
في حالة البيانات غير المبوبة
نتبع الخطوات التالية:
- نرتب البيانات تصاعدياً أو تنازلياً.
- نوجد ترتيب القسيم المطلوب حسابه (,إيجاد ترتيب القسيم مشروح فيما بعد).
- القسيم المطلوب هو المشاهدة التي يكون ترتيبها هو ترتيب القسيم نفسه.
- إذا وقع ترتيب القسيم بين قيمتين فيكون قيمة هذا القسيم هو متوسط هاتين القيميتن.
في حال البيانات المبوبة في جداول إحصائية تكرارية
نتبع الخطوات التالية:
- ننشىء جدولاً تكرارياً تراكميا (تجمعياً) صاعداً أو هابطاً.
- نحدد فئة القسيم، وهي الفئة التي يقع ضمنها ترتيب القسيم المطلوب والذي يحسب تماماً كما في حالة البيانات غير المبوبة.
- يحسب بعد ذلك القسيم المطلوب وفق إحدى العلاقتين التاليتين، وذلك بحسب الجدول التكراري التجمعي المختار (صاعداً أم هابطاً):
- إذا كان صاعداً يحسب بالعلاقة التالية:
- إذا كان هابطاً يحسب بالعلاقة التالية:
حيث:
- L1: هو عبارة عن الحد الأدنى لفئة القسيم.
- L2: هو عبارة عن الحد الأعلى لفئة القسيم.
- n: هو عدد البيانات (حجم العينة).
- fi: هو تكرار فئة القسيم.
- : التكرار التراكمي للفئة السابقة لفئة القسيم.
- : التكرار التراكمي للفئة التالية لفئة القسيم.
- c: طول فئة القسيم.
- X: هو ترتيب القسيم المطلوب حسابه.
الثليث
هي المشاهدات التي تقسم البيانات إلى ثلاثة أقسام متساوية يحتوي كل منها على 33,33% من المشاهدات.
ترتيب الثلثيات
- الثليث الأول يحصر خلفه 33,33% من البيانات، وترتيبه هو: .
- الثليث الثاني يحصر خلفه 66,66% من البيانات، وترتيبه هو: .
الاستخدامات العملية للثليث
الربيعات
هي المشاهدات التي تقسم البيانات إلى أربعة أقسام متساوية، كل منها يحوي 25% من البيانات.
ترتيب الربيعات
- الربيع الأول يحصر خلفه 25% من البيانات، وترتيبه هو:
- الربيع الثاني يحصر خلفه 50% من البيانات، وترتيبه هو: (وهو نفسه الوسيط).
- الربيع الثالث يحصر خلفه 75% من البيانات، وترتيبه هو: .
الاستخدامات العملية للربيعات
تقدير الربيعيات لتعداد
أنواع التقدير تتضمن:
| النوع | h | Qp | ملاحظات |
|---|---|---|---|
| R-1, SAS-3 | Inverse of empirical distribution function. When p = 0, use x1. | ||
| R-2, SAS-5 | The same as R-1, but with averaging at discontinuities. When p = 0, x1. When p = 1, use xN. | ||
| R-3, SAS-2 | The observation numbered closest to Np. Here, ⌊ h ⌉ indicates rounding to the nearest integer, choosing the even integer in the case of a tie. When p ≤ (1/2) / N, use x1. | ||
| R-4, SAS-1 | Linear interpolation of the empirical distribution function. When p < 1 / N, use x1. When p = 1, use xN. | ||
| R-5 | Piecewise linear function where the knots are the values midway through the steps of the empirical distribution function. When p < (1/2) / N, use x1. When p ≥ (N - 1/2) / N, use xN. | ||
| R-6, SAS-4 | Linear interpolation of the expectations for the order statistics for the uniform distribution on [0,1]. When p < 1 / (N+1), use x1. When p ≥ N / (N + 1), use xN. | ||
| R-7, Excel | Linear interpolation of the modes for the order statistics for the uniform distribution on [0,1]. When p = 1, use xN. | ||
| R-8 | Linear interpolation of the approximate medians for order statistics. When p < (2/3) / (N + 1/3), use x1. When p ≥ (N - 1/3) / (N + 1/3), use xN. | ||
| R-9 | The resulting quantile estimates are approximately unbiased for the expected order statistics if x is normally distributed. When p < (5/8) / (N + 1/4), use x1. When p ≥ (N - 3/8) / (N + 1/4), use xN. | ||
| If h were rounded, this would give the order statistic with the least expected square deviation relative to p. When p < (3/2) / (N + 2), use x1. When p ≥ (N + 1/2) / (N + 2), use xN. |
لاحظ أن R-3 and R-4 لا يعطون h = (N + 1) / 2 عندما تكون p = 1/2.
الخميسات
هي المشاهدات التي تقسم البيانات إلى 5 أقسام متساوية كل منها يحوي 20% من البيانات.
ترتيب الخميسات
- الخميس الأول يحصر خلفه 20% من البيانات، وترتيبه هو .
- الخميس الثاني يحصر خلفه 40% من البيانات، وترتيبه هو .
- الخميس الثالث يحصر خلفه 60% من البيانات، وترتيبه هو .
- الخميس الرابع يحصر خلفه 80% من البيانات، وترتيبه هو .
الاستخدامات العملية للخميسات
التسيعات
هي المشاهدات التي تقسم البيانات إلى تسعة أقسام متساوية، يحوي كل منها 11,11% من البيانات.
ترتيب التسيعات
| رقم التسيع | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| ترتيب التسيع | ||||||||
| المساحة التي يحصرها خلفه | 11,11% | 22,22% | 33,33% | 44,44% | 55,55% | 66,66% | 77,77% | 88,88% |
الاستخدامات العملية للتسيعات
عشريات
هل المشاهدات التي تقسم البيانات إلى عشرة اقسام متساوية، يحوي كل منها 10% من البيانات.
ترتيب العشريات
| رقم العشري | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| ترتيب العشري | (وهو نفسه الوسيط) | ||||||||
| المساحة التي يحصرها خلفه | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% |
الاثنا عشريات
الميئينات
اقرأ أيضاً
- مقاييس النزعة المركزية.
- مقاييس التشتت.
- وسيط.
- عشريات.
- مئينات.
- Summary statistics
- Descriptive statistics
- Quartile
- Q-Q plot
- Quantile function
- Quantile normalization
المراجع
روابط خارجية
- Quartile - from MathWorld Includes references and compares various methods to compute quartiles
- Quartiles - From MathForum.org
- Quartiles - An example how to calculate it








































