النقل البُعدي الكمومي

النقل البُعدي الكمومي Quantum teleportation، أو entanglement-assisted teleportation، هي عملية by which a qubit (the basic unit of quantum information) can be transmitted exactly (in principle) from one location to another, without the qubit being transmitted through the intervening space. It is useful for quantum information processing, however it does not immediately transmit classical information, and therefore cannot be used for communication at superluminal (faster than light) speed. Quantum teleportation is unrelated to the common term teleportation - it does not transport the system itself, and does not concern rearranging particles to copy the form of an object.

•  مقالة مفصلة: إبتكار تقنى ..الإنتقال البعدى الكمومي

أصبح حلم الخيال العلمي في "بث" الأشياء من مكان إلى

آخر أمرا واقعا ـ على الأقل بالنسبة إلى جسيمات الضوء.

أ. زايلنگر

المشهد مشهد مألوف من مشاهد أفلام وتلفزة الخيال العلمي: جماعة جسورة من المستكشفين تدخل حجرة خاصة، فتومض الأضواءُ وتصدح التأثيرات الصوتية ويختفي أبطالنا من الوجود ليظهروا على سطح كوكب بعيد. هذا هو حلم النقل (الانتقال) البعدي teleportation ـ أي المقدرة على الانتقال من مكان إلى آخر من دون الاضطرار لقطع المسافات الطويلة المملة بينهما، وذلك باستخدام وسيلة نقل مادية خاصة. ومع أن النقل البعدي للأجسام الكبيرة أو للبشر لا يزال أمرا خياليّا إلا أن النقل البعدي الكمومي صار حقيقة مختبرية بالنسبة إلى الفوتونات: جسيمات الضوء المفردة.

يستغل النقل البعدي الكمومي بعضا من الخواص الأساسية جدا والغريبة للميكانيك الكمومي، ذلك الفرع من الفيزياء الذي اختُرع في الربع الأول من القرن العشرين لتفسير السيرورات التي تحدث على مستوى الذرات المفردة. وقد أدرك النظريون منذ البداية أن الفيزياء الكمومية أدت إلى فيض من الظواهر الجديدة التي يتحدى بعضها الحس السليم. وقد مكّن التقدم التقاني في الربع الأخير من القرن العشرين الباحثين من إجراء كثير من التجارب التي لا تبين فقط الجوانب الأساسية، والغريبة أحيانا، للميكانيك الكمومي وإنما تطبقها أيضا، كما في حالة النقل البعدي الكمومي، وذلك للتوصل إلى أمور فذَّة لم يكن بالمستطاع تصورها فيما مضى.

يصل المسافرون إلى المحطة المركزية الكبرى للنقل البعدي. وعلى الرغم من أن النقل البعدي للأشياء الكبيرة، ناهيك عن الكائنات الحية، لن يكون ممكنا إلا في الخيال فإن النقل البعدي للحالات الكمومية الأولية قد أجري فعلا.

في قصص الخيال العلمي يتيح النقل البعدي عادة السفر بصورة آنية instantaneous مما يخرق حد السرعة الذي وضعه آينشتاين في نظرية النسبية والقائل إنه لا يمكن لأي شيء أن ينتقل بسرعة أكبر من سرعة الضوء [انظر: "أسرع من الضوء؟"، مجلة العلوم، العدد 2 (1995) ، ص 58]. والنقل البعدي أقل إزعاجا من أية وسيلة عادية للرحلات الفضائية. ويقال إن G. رودنْبِرِي ، مبدع الهجرة إلى النجوم Star Trek، اعتبر "الحزمة الضوئية الناقلة" وسيلة للاقتصاد في تكاليف محاكاة الهبوط على كواكب غريبة والإقلاع منها.

تختلف إجراءات النقل البعدي في الخيال العلمي من قصة إلى أخرى، لكنها تسير بصورة عامة كما يلي: يعمل جهاز على مسح scan الشيء الأصلي لكي يستخلص جميع المعلومات اللازمة لتوصيفه. ثم يقوم جهاز إرسال ببث المعلومات إلى محطة الاستقبال حيث تستخدم للحصول على نسخة دقيقة من الأصل. وفي بعض الحالات تُرسل المادة التي يتكون منها الأصل أيضا إلى محطة الاستقبال، ربما على شكل "طاقة" من نوع ما، وفي حالات أخرى تصنع النسخة من الذرات والجزيئات الموجودة أصل في محطة الاستقبال.

يبدو أن الميكانيك الكمومي يحول، من حيث المبدأ، دون تحقيق النقل البعدي. ذلك أن مبدأ الارتياب (عدم التحديد) لهايزنبرگ يقتضي أنه لا يمكن معرفة الموضع الدقيق لجسم ما وزخمه momentum في الوقت نفسه، ومن ثم لا يمكن إجراء مسح كامل للشيء المراد نقله نقل بعديا، إذ إن موقع أو سرعة كل ذرة وإلكترون سيكون عرضة للخطأ. ولما كان مبدأ الارتياب لهايزنبرگ يطبق أيضا على أزواج أخرى من المقادير فإنه يستحيل قياس الحالة الكمومية الكلية بدقة لأي شيء بصورة مؤكدة، علما أن مثل هذه القياسات ضرورية للحصول على المعلومات اللازمة لوصف الأصل وصفا دقيقا. (أما في "هجرة إلى النجوم" فإن "معوّض هايزنبرگ" Heisenberg Compensator يتغلب بصورة ما، أشبه بالمعجزة، على هذه الصعوبة.)

وفي عام 1993 قلب فريق من الفيزيائيين هذه الحكمة التقليدية حين اكتشف طريقة لاستخدام الميكانيك الكمومي نفسه في النقل البعدي. وقد وجد الفريق المكوّن من H .C. بينيت [من شركة IBM] و G. براسار و C. كريپو و<. جوزا [من جامعة مونتريال] وA. بيريز [من معهد تخنيون التقاني] و K .W. ووتَّرز [من كلية وليامز] أن خاصة غريبة إنما أساسية من خواص الميكانيك الكمومي، وهي التشابك entanglement، يمكن أن تستخدم للالتفاف حول القيود التي يضعها مبدأ الارتياب لهايزنبرگ دون خرقه.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تشابك

نحن في عام 2100، وقد أحضر لك صديق، يهوى اللعب بالفيزياء والحيل المسلية، مجموعة من أزواج حجر النرد. وطلب إليك أن ترميها مرة واحدة، كل زوج وحده. تمسك بحذر بالزوج الأول وأنت تتذكر الإخفاق التام بالنسبة إلى الثقب الأسود المكروي في عيد الميلاد (1999). وأخيرا ترمي حجري النرد وتحصل على 3 مزدوجة. ثم ترمي الزوج الثاني فتجد 6 مزدوجة. ثم التالي: 1 مزدوج. الحجران يتماثلان دائما.

تسلك أحجار النرد في هذه الحكاية وكأنها جسيمات كمومية متشابكة. فكل حجر بمفرده عشوائي ولا عيب فيه لكن شريكه المتشابك معه يعطي دائما، بطريقة ما، الرقم نفسه الذي يعطيه الحجر الأول. وقد بُرهن على مثل هذا السلوك ودُرس دراسة مكثفة بالنسبة إلى جسيمات متشابكة حقيقية. ففي تجارب نموذجية تقوم أزواج من الذرات أو الأيونات أو الفوتونات مقام حجري النرد، وتقوم خواص مثل الاستقطاب مقام أوجه حجر النرد المختلفة.

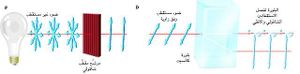
لننظر في حالة فوتونين استقطاباهما متشابكان. فهما عشوائيان إنما متطابقان. تتألف الحزم الضوئية، وحتى الفوتونات المفردة، من اهتزازات الحقول الكهرمغنطيسية، ويشير الاستقطاب إلى تراصف اهتزازات الحقل الكهربائي [انظر الشكل العلوي في الصفحة 40]. لنفترض أن لدى الآنسة سمر أحد الفوتونين المتشابكين وأن لدى السيد أحمد شريكه الآخر. حين تقيس سمر فوتونها لترى إذا كان مستقطبا بصورة شاقولية أو أفقية فإن لكل نتيجة قياس احتمال قدره 50 في المئة. ولدى فوتون أحمد الاحتمالان نفساهما، لكن التشابك يؤمّن له الحصول على نتائج سمر نفسها بالضبط. فحالما تحصل سمر على النتيجة "أفقي" مثل تعرف أن فوتون أحمد سيكون مستقطبا استقطابا أفقيّا. أما قبل أن تجري سمر القياس فلم يكن لأي من الفوتونين استقطاب خاص؛ والحالة المتشابكة تحدد فقط أن قياسا ما سيجد أن الاستقطابين متساويان.

والسمة المدهشة لهذه السيرورة هي أنه ليست هناك أية أهمية لكون سمر وأحمد بعيدا أحدهما عن الآخر، فالعملية تسير مادام تشابك فوتونيهما قائما. وحتى لو كانت سمر على نجم ألفا قنطورس وكان أحمد على كوكب الأرض فإن نتائجهما ستتفق حين يقارنان فيما بينها. ففي كل مرة تجري الأمور كما لو أن فوتون أحمد يتأثر بصورة سحرية بالقياس الذي تجريه سمر من مسافة بعيدة، والعكس بالعكس.

ويمكنكم أن تتساءلوا فيما لو كان بالإمكان أن نفسر التشابك بأن نتخيل أن كل جسيم يحمل في داخله بعض التعليمات المسجلة. لعلنا حين نشابك الجسيمين فإننا نزامن آلية خفية ما في داخلهما تحدد النتائج التي سيعطيانها حين يجري القياس عليهما. وسيكون ذلك كافيا لتفسير الأثر الغامض للقياس الذي تجريه سمر في جسيم أحمد. إلا أن الفيزيائي الإيرلندي < J. بِل> قدم في الستينات من القرن العشرين مبرهنة تقول إن مثل هذا التفسير المعتمد على "المتحولات الخفية" ينبغي أن يؤدي في حالات معينة إلى نتائج مختلفة عن تلك التي يتنبأ بها الميكانيك الكمومي المتعارف (السائد). وقد أثبتت التجارب توقعات الميكانيك الكمومي بدقة عالية جدّا.

وكان الفيزيائي النمساوي <E. شرودينگر>، أحد مبتكري الميكانيك الكمومي، قد وصف التشابك بأنه "السمة الرئيسية" للفيزياء الكمومية. وكثيرا ما يدعى التشابك "الأثر (المفعول) EPR" وتدعى الجسيمات "أزواج EPR" نسبة إلى كل من آينشتاين و< B. بودولسكي> و< N. روزِن> الذين حللوا في عام 1935 مظاهر التشابك المؤثر عبر مسافات كبيرة. وكان آينشتاين يتحدث عنه وكأنه "فعل شبحي عن بعد". فلو حاول أحد أن يفسر النتائج على أنها إشارات تنتقل بين الفوتونين لكان على الإشارات أن تنتقل بسرعة أكبر من سرعة الضوء. وقد تساءل كثيرون، بطبيعة الحال، عما إذا كان من الممكن استعمال هذا الأثر لنقل المعلومات بسرعة تفوق سرعة الضوء.

ولكن للأسف فإن القواعد الكمومية لا تسمح بذلك. فكل قياس محلي يجري على فوتون منعزل، يُنتج نتيجة عشوائية تماما ولا يحمل من ثم أية معلومات من الموقع البعيد. وهو لا يخبرنا إلا بما يمكن أن تكون عليه احتمالات نتيجة القياس البعدي اعتمادا على ما تم قياسه هناك. ومع ذلك يمكننا أن نستفيد من التشابك بطريقة بارعة للوصول إلى النقل البعدي الكمومي.

 الاستفادة من الفوتونات المتشابكة

يخطط أحمد وسمر للقيام بعملية نقل بعدي لفوتون، ولدى التحضير لذلك يتشاركان في زوج مساعد متشابك من الفوتونات فتأخذ سمر الفوتون A، في حين يأخذ أحمد الفوتون B. وبدل من إجراء قياس عليهما يقوم كل منهما بخزن فوتونه من دون أن يشوش حالة التشابك المرهفة [انظر الشكل العلوي في الصفحة 42].

تملك سمر، في الوقت المناسب، فوتونا ثالثا ـ ولنسمّه الفوتون X ـ تريد أن تنقله نقل بعديّا إلى أحمد. وهي لا تعرف ما حالة الفوتون X، ومع ذلك تريد أن يكون لدى أحمد فوتون بالاستقطاب نفسه الذي لـ X. إلا أنها لا تستطيع ببساطة أن تقيس استقطاب الفوتون وترسل النتيجة إلى أحمد، لأن نتيجة قياسها، على العموم، لن تكون مطابقة لحالة الفوتون الأصلية. وهذه نتيجة لمبدأ الارتياب لهايزنبرگ.

يتألف الضوء غير المستقطَب من فوتونات مستقطَبة في جميع الاتجاهات (a). أما في الضوء المستقطب فتقع اهتزازات الحقل الكهربائي للفوتونات (الأسهم) كلها على استقامة واحدة. تشطر بلورة الكالسيت (b) حزمة الضوء إلى اثنتين فترسل الفوتونات المستقطبة استقطابا موازيا لمحورها في حزمة وتلك المستقطبة بصورة معامدة في الحزمة الأخرى. أما الفوتونات المستقطبة حسب الزوايا الواقعة بين هذه وتلك فهي في تراكب كلتيهما معا. ويمكن كشف كل فوتون منها في إحدى الحزمتين باحتمال يتعلق بالزاوية. ومادام الأمر يتعلق بالاحتمالات فإننا لا نستطيع قياس الاستقطاب المجهول لفوتون مفرد بصورة مؤكدة.

وبدل من ذلك تقوم سمر، لنقل الفوتون X نقل بعديّا، بإجراء قياس عليه وعلى الفوتون A معا من دون أن تحدد استقطاب كل منهما على حدة. وقد تجد، على سبيل المثال، أن استقطابيهما "متعامدان" (لكنها تبقى جاهلة بالاستقطاب المطلق لأي منهما على أية حال). ومن الناحية الفنية يدعى القياس المشترك للفوتونين A وX قياس حالة بِل. ويولّد القياس الذي أجرته سمر أثرا خفيّا: فهو يغير فوتون أحمد بصورة يصبح معها متناسبا مع تآلف يجمع بين نتيجة قياسها وبين الحالة التي كان فيها الفوتون X أصل. وفي الحقيقة يحمل فوتون أحمد الآن حالة فوتون سمر X، إما بالضبط أو بصورة معدلة بطريقة بسيطة.

يمكن أن يبدأ النقل البعدي الكمومي لشخص ما (وهو أمر مستحيل عمليّا لكنه مثال جيد لمساعدة التخيل) بوضعه داخل حجرة القياس (في اليسار) وإلى جانبه كتلة مساوية من المادة المساعدة (الأخضر)، بعد أن تكون المادة المساعدة قد شبكت كموميا بنظيرتها الموجودة في محطة الاستقبال البعيدة (في اليمين)

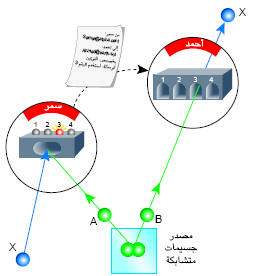
ولإتمام عملية النقل البعدي يجب أن ترسل سمر إلى أحمد، رسالة تنقل بالطرق العادية، مثل اتصال هاتفي أو ملاحظة مكتوبة على قصاصة من الورق. ويستطيع أحمد، إن لزم الأمر بعد أن يتلقى هذه الرسالة، أن يحول الفوتون B بحيث يصبح في النهاية نسخة مطابقة تماما للفوتون X الأصلي. أما التحويل الذي ينبغي لأحمد أن يجريه فيتوقف على نتيجة قياس سمر.

وهناك أربعة إمكانات تقابل أربع علاقات كمومية بين الفوتونين A وX. وأحد التحويلات النموذجية التي ينبغي لأحمد أن يجريها على فوتونه هو تغيير استقطابه 90 درجة، وهذا ما يمكن عمله بإمرار الفوتون عبر بلورة تتمتع بالخواص الضوئية المناسبة.

أما النتيجة التي تحصل عليها سمر من الإمكانات الأربع فهي أمر عشوائي تماما ومستقل عن حالة X الأصلية. لذلك فإن أحمد لا يعرف كيف يعالج فوتونه ما لم يحصل على نتيجة قياس سمر. ويمكن القول إن فوتون أحمد يحوي آنيا جميع المعلومات، من فوتون سمر الأصلي، التي انتقلت إليه بوساطة الميكانيك الكمومي. وعلى أحمد، لكي يعرف كيف يقرأ هذه المعلومات، أن ينتظر وصول المعلومات الكلاسيكية، المؤلفة من بتتين bits لا تستطيعان الانتقال بسرعة أكبر من سرعة الضوء.

تنشأ أزواج الفوتونات المتشابكة حين تمر حزمة ليزر خلال بلورة مثل بلورات الباريوم بيتا. ويمكن للبلورة أحيانا أن تحول فوتونا فوق بنفسجي واحدا إلى فوتونين ذوي طاقة أخفض أحدهما مستقطب شاقوليا (على المخروط الأحمر) والآخر مستقطب أفقيا (على المخروط الأزرق). فلو حدث وسار الفوتونان وفق تقاطع المخروطين (اللون الأخضر) لما كان لأي منهما استقطاب محدد، لكن استقطابيهما النسبيين متتامان؛ وبالتالي فالفوتونان متشابكان. والصورة الملونة (في اليمين) هي صورة فوتوغرافية للضوء المحول تخفيضيّا down-converted. ولا تمثل الألوان هنا لون الضوء.

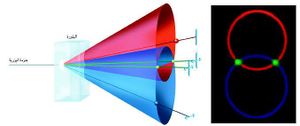
يمكن للمرتابين (الشكوكيين) أن يدّعوا أن الشيء الوحيد الذي نقل نقل بعديّا هو حالة استقطاب الفوتون، أو بصورة أعم، حالته الكمومية، وليس الفوتون "نفسه". ولكن لما كانت الحالة الكمومية لفوتون ما هي مواصفاته المميزة له، فإن النقل البعدي لحالته مكافئ تماما لنقل الجسيم بعديّا [انظر ما هو مؤطر في الصفحة 45].

لنلاحظ أنه لا تنتج من النقل البعدي الكمومي نسختان من الفوتون X. ويمكن نسخ المعلومات الكلاسيكية قدر ما نريد من المرات، لكن النسخ الكامل (طبق الأصل) للمعلومات الكمومية مستحيل، وهذا ما يعرف بمبرهنة عدم الاستنساخ no-cloning، وكان قد أثبتها <ووتّرز> و<H .W. زوريك> [من مختبر لوس ألاموس الوطني] في عام 1982. (لو كان بإمكاننا استنساخ حالة كمومية لتمكنا من استخدام المستنسخات لخرق مبدأ هايزنبرگ).

قياس كمومي ... إن القياس المشترك الذي يجري على المادة المساعدة وعلى الشخص (في اليسار) يحولهما إلى حالة كمومية عشوائية، وينتج كمية كبيرة من البيانات العشوائية (لكنها بالغة الأهمية) ـ بتّتان لكل حالة أولية. كما يغير القياس آنيا الحالة الكمومية للمادة النظيرة البعيدة (في اليمين) بوساطة "الفعل الشبحي عن بعد."

 الالتفاف حول هايزنبرگ

إضافة إلى ذلك فإن حالة الفوتون X حُوِّلت إلى أحمد دون أن تعرف سمر أو يعرف أحمد ماهية هذه الحالة. فنتيجة قياس سمر لا تُعْلِمهما أي شيء عن الحالة مادامت نتيجة عشوائية تماما. وهذه هي الطريقة التي تلتف بها العملية حول مبدأ هايزنبرگ الذي يمنعنا من تحديد الحالة الكمومية التامة لجسيم ما، ولكنه لا يحول دون النقل البعدي للحالة التامة ما دمنا لا نحاول أن نرى ما هي هذه الحالة!

وكذلك فإن المعلومات الكمومية المنقولة بعديّا لا تنتقل ماديا من سمر إلى أحمد. فكل ما ينتقل ماديا هو الرسالة حول نتيجة قياس سمر التي تخبر أحمد كيف ينبغي أن يعالج فوتونه ولكنها لا تحمل أية معلومات حول حالة الفوتون X نفسه

يعتمد النقل البعدي الكمومي المثالي على سمر (المرسل) وأحمد (المستقبل) اللذين يتشاركان في زوج من الجسيمات المتشابكة A و B (الأخضر). لدى سمر جسيم في حالة كمومية مجهولة X (الأزرق). تجري سمر قياس حالة بِل على الجسيمين A و X فتنتج واحدة من أربع نتائج ممكنة، وتخبر أحمد بالنتيجة بالوسائل العادية. وتبعا لنتيجة سمر فإما أن يدع أحمد جسيمه من دون تعديل (1) أو يديره (2، 3، 4). وفي جميع الحالات يصبح الجسيم نسخة مطابقة تماما للجسيم الأصلي X.

وفي حالة واحدة من أربع حالات تكون سمر محظوظة بقياسها ويصبح فوتون أحمد في الحال نسخة مطابقة لفوتون سمر الأصلي. يمكن أن يبدو الأمر وكأن المعلومات انتقلت آنيا من سمر إلى أحمد متجاوزة حد آينشتاين للسرعة. ومع ذلك فإن هذه الصفة الغريبة لا يمكن أن تستخدم لإرسال المعلومات، لأنه ليست لدى أحمد أية وسيلة لمعرفة أن فوتونه صار نسخة مطابقة. وعندما يعرف أحمد نتيجة قياس سمر لحالة بِل، هذه النتيجة التي ترسل إليه بالوسائل الكلاسيكية، عندئذ فقط يستطيع استغلال المعلومات في الحالة الكمومية المنقولة بُعديا. لنفترض أنه يحاول أن يخمّن الحالات التي كان فيها النقل البعدي ناجحا في الحال. سيخطئ في 75 في المئة من تخميناته ولن يعرف أية تخمينات كانت صحيحة. وإذا استخدم الفوتونات معتمدا على مثل هذه التخمينات فستكون النتائج مماثلة لتلك التي كان يحصل عليها فيما لو أخذ حزمة من الفوتونات استقطاباتها عشوائية. وهكذا تنتصر نسبية آينشتاين، إذ يفشل الفعل الشبحي الآني الكمومي عن بعد في إرسال معلومات مفيدة بسرعة أكبر من سرعة الضوء.

يمكن أن يبدو المقترح النظري الموصوف آنفا وكأنه رَسمَ مخططا واضحا لبناء ناقل بعدي teleporter، لكنه على العكس من ذلك قدم تحديّا تجريبيّا كبيرا. لقد أصبح إنتاج أزواج متشابكة من الفوتونات عمل روتينيا في التجارب الفيزيائية في العقد الماضي، لكن إجراء قياس حالة بِل على فوتونين مستقلين لم يسبق له أن نفّذ قط من قبل.

 بناء ناقل بُعدي

إن إحدى الطرائق الفعالة لإنتاج أزواج متشابكة من الفوتونات هي التحويل التخفيضي الوسيطي التلقائي spontaneous parametric down-conversion: إذا مرر فوتون مفرد عبر بلورة خاصة فإنه يولّد أحيانا فوتونين جديدين يكونان متشابكين بحيث يبديان استقطابين متعاكسين حين يقاسان [انظر الشكل العلوي في الصفحة 41].

بث البيانات العشوائية... ينبغي أن ترسل بيانات القياس إلى محطة الاستقبال البعيدة بالوسائل التقليدية. ولما كان هذا الإجراء محدودا بسرعة الضوء فإن النقل البعدي لشخص ما بسرعة أكبر من سرعة الضوء أمر مستحيل

زاوية المرتابين

إجابات المؤلف عن الأسئلة المألوفة المتعلقة بالنقل البعدي

ألَيْس من المبالغة أن ندعو هذا نقل بعديّا؟ فما نُقل نقل بعديّا، في نهاية المطاف ليس سوى حالة كمومية وليس جسما حقيقيّا. يطرح هذا السؤالُ السؤالَ الفلسفي الأعمق حول ما نعنيه بالهوية. فكيف نعرف أن شيئا ما ـ وليكن السيارة التي نجدها في مرآبنا صباحا ـ هو الشيء نفسه الذي رأيناه منذ برهة خلت؟ مادام له جميع الأوصاف والخواص الصحيحة. إن الفيزياء الكمومية تؤكد هذه النقطة: فالجسيمات من النوع نفسه وفي الحالة الكمومية ذاتها لا متمايزة حتى من حيث المبدأ. فلو استطاع المرء مقايضة ذرات الحديد في السيارة بذرات حديد من كومة خامات وتمكَّن من إعادة تشكيل الحالات الكمومية للذرات بالضبط لكانت النتيجة النهائية مطابقة، في أعمق المستويات، للسيارة الأصلية. فالهوية لا يمكن أن تعني أكثر مما يلي: أن يكون الشيء مماثل في جميع خواصه.

أَلَيْس الأمر أشبه "بالفاكس الكمومي"؟ إن إرسال فاكس يولد نسخة يسهل تمييزها عن الأصل، في حين لا يمكن تمييز الشيء المنقول نقل بعديّا حتى من حيث المبدأ. أضف إلى ذلك أن الأصل يجب أن يُدمر في حالة النقل البعدي الكمومي.

هل يمكن أن نأمل بالفعل بنقل شيء معقّد نقل بعديّا؟ هناك العديد من العوائق الصعبة. أول يجب أن يكون الشيء في حالة كمومية صافية، ومثل هذه الحالات هشة جدا. لا تتآثر الفوتونات مع الهواء كثيرا، ولذلك يمكن أن نجري تجاربنا في أمكنة مفتوحة، لكن التجارب التي تستخدم الذرات والأجسام الكبيرة يجب أن تجرى في الخلاء vacuum لتجنب التصادمات مع جزيئات الغاز. أضف إلى ذلك أنه كلما كان الجسم كبيرا كان من الأسهل إحداث اضطراب في حالته الكمومية. إن كتلة صغيرة جدّا من المادة يمكن أن يسبب اضطرابها حتى الإشعاع الحراري الصادر عن جدران الأجهزة. وهذا هو السبب في أننا لا نرى عادة الآثار الكمومية في عالمنا اليومي.

لقد بُرهن تجريبيّا على التداخل الكمومي، وهو أثر توليده أسهل من التشابك أو النقل البعدي، باستخدام الكرات المؤلفة من 60 ذرة كربون. ومثل هذا العمل سوف يتطور نحو أجسام أكبر، ربما حتى الڤيروسات الصغيرة، ولكن لا تحبسوا أنفاسكم وتظنوا أنه يمكن أن يكرر باستخدام أجسام في حجم كرات القدم!

والمشكلة الأخرى هي قياس حالة بِل. ماذا يمكن أن يعني إجراء قياس حالة بِل على ڤيروس مؤلف من 107 ذرة مثل؟ كيف يمكن أن نستخلص 108 من بتات المعلومات التي يولدها مثل هذا القياس؟ أما بالنسبة إلى جسم لا يتعدى عدة غرامات فيصبح العدد مستحيل: 1024 بتة من البيانات.

هل سيتطلب النقل البعدي للإنسان الدقة الكمومية؟ لا يبدو أن كون شخص ما في الحالة الكمومية نفسها أمر ضروري لأن يكون هو الشخص ذاته. فنحن نغير حالاتنا طوال الوقت ونبقى الأشخاص ذاتها ـ على الأقل بقدر ما نعلم! وعلى العكس من ذلك فإن التوأمين المتطابقين، أو النسيلتين البيولوجيتين، ليسا "الشخص ذاته" لأن لديهما ذاكرتين مختلفتين. فهل يمنعنا ارتياب هايزنبرگ من نسخ شخص بصورة دقيقة تكفي لأن تجعله يعتقد أنه مثل الأصل تماما؟ لا أحد يعلم. من المثير للاهتمام على أية حال أن مبرهنة عدم الاستنساخ الكمومية تمنعنا من صنع نسخ كاملة الدقة من شخص ما.

لو نقلنا جسم شخص نقل بعديّا، فهل يبقى العقل في مكانه الأول؟

لا شك في أننا قد نستطيع استخدام التقانة المتوفرة حاليا للنقل البعدي للحالات الأولية elementary، كمثل حالات الفوتون في تجربتنا، عبر مسافات تبلغ عدة كيلومترات، وقد نوصلها إلى السواتل (الأقمار الصنعية). فالتقانة التي تسمح بنقل حالات الذرات المفردة متاحة الآن: فقد برهنت المجموعة التي يقودها < S. آروش> في المدرسة العليا للأساتذة في باريس على تشابك الذرات. ومن المعقول أن نتوقع تشابك الجزيئات ومن ثم نقلها نقل بعديّا خلال العقد الأول من القرن الحادي والعشرين. أما ما يحدث بعد ذلك فمتروك لخيال من يشاء.

قد يكون مجال الحوسبة الكمومية أحد أهم تطبيقات النقل البعدي، حيث يعمَّم المفهوم العادي للبتات (الأصفار والواحدات) إلى البتات الكمومية qubits، التي يمكن أن توجد بشكل تراكبات وتشابكات من الأصفار والواحدات. وربما أمكن استخدام النقل البعدي لتبادل المعلومات الكمومية فيما بين المعالِجات الكمومية. كما يمكن للنواقل البعدية الكمومية أن تقوم بدور مكونات أساسية لبناء حاسوب كمومي [انظر ما هو مؤطر في الصفحة 46].

ربما كان الميكانيك الكمومي إحدى أعمق النظريات التي اكتُشِفت حتى الآن. وقد دفعت المسائل التي يطرحها أمام حدسنا اليومي بآينشتاين إلى انتقاد الميكانيك الكمومي بشدة. فقد كان يصر على أن مهمة الفيزياء هي محاولة فهم وإدراك الواقع القائم مستقل عن رصدنا له. ومع ذلك فقد كان يعرف جيدا أننا سنقع في مشكلات عميقة عندما نحاول إعطاء حقيقة فيزيائية لكل فرد من الزوج المتشابك. أما نظيره الفذ، الفيزيائي الدنمركي <N. بور>، فقد كان يصر على ضرورة أخذ المنظومة جميعها بعين الاعتبار ـ أي ترتيب كل الجسيمين معا في حالة الزوج المتشابك. وما أمنية آينشتاين في أن تكون لكل جسيم حالة حقيقية مستقلة سوى شيء خال من أي معنى

 الحواسيب الكمومية

لعل أكثر تطبيقات النقل البعدي الكمومي واقعية ـ عدا البحث الفيزيائي البحت ـ هو في مجال الحوسبة الكمومية.إن الحاسوب الرقمي العادي يتعامل مع البتات التي تأخذ إحدى قيمتين محددتين 0 أو 1، لكن الحاسوب الكمومي يستخدم البتات الكمومية [انظر: "الحوسبة الكمومية باستخدام الجزيئات"،مجلة العلوم، العددان 8/9 (1999) ، ص 36]. يمكن للبتات الكمومية أن تكون في تراكبات كمومية من 0 و1 تماما مثلما يمكن للفوتون أن يكون في تراكب من الاستقطابين الأفقي والشاقولي. وفي الواقع يبث الناقل البعدي الكمومي الأساسي، لدى إرسال فوتون مفرد، بتة كمومية واحدة من المعلومات.

قد تبدو تراكبات الأعداد غريبة، لكن كما قال عنها <R. لانداور> من الشركة IBM: "حين كنا أطفال صغارا كنا نتعلم كيف نعدّ على أصابعنا الدبقة الكلاسيكية، ولم نكن نعرف شيئا عن الميكانيك الكمومي وعن التراكبات، فاكتسبنا الحدس الخاطئ، واعتقدنا أن المعلومات كلاسيكية. وظننا أنه بإمكاننا رفع ثلاث أصابع، ثم أربع. ولم نكن ندرك أنه يمكن أن يكون هناك تراكب منهما معا."

يمكن للحاسوب الكمومي أن يؤثر في تراكب العديد من المدخلات المختلفة دفعة واحدة. فهو، على سبيل المثال، يمكن أن يشغّل خوارزمية algorithm لمليون من المدخلات في آن واحد مستخدما عددا من البتات الكمومية يساوي عدد البتات التي يحتاج إليها حاسوب عادي لتشغيل الخوارزمية مرة واحدة في مدخل واحد. وقد برهن النظريون على أن الخوارزميات المُشغَّلة على الحواسيب الكمومية يمكنها أن تحل بعض المسائل بصورة أسرع (أي في عدد أقل من الخطوات الحاسوبية) مما تستطيعه أية خوارزمية معروفة تُشَغَّل على حاسوب كلاسيكي. وتشتمل هذه المسائل على إيجاد مفردات في قاعدة البيانات وتحليل الأعداد الكبيرة إلى عوامل، مما له أهمية كبيرة في فك الكودات السرية.

ولم تُبْنَ حتى الآن سوى العناصر البدائية جدّا من الحواسيب الكمومية: بوابات منطقية يمكنها أن تعالج بتة كمومية واحدة أو اثنتين. ولا يزال صنع حاسوب كمومي صغير أمرا بعيد المنال. فإحدى المشكلات الأساسية هي نقل البيانات الكمومية نقل موثوقا بين مختلف البوابات المنطقية أو المعالجات سواء كان ذلك داخل حاسوب كمومي واحد أو عبر شبكات كمومية. والنقل البعدي الكمومي هو أحد الحلول.

وإضافة إلى ما سبق فقد برهن D. گوتِسْمان [من الشركة مايكروسوفت]

و L .I تشوانگ [من الشركة IBM] حديثا أن حاسوبا كموميّا عمومي الغرض general-purpose quantum computer يمكن أن يُبنى من ثلاثة مكونات أساسية: جسيمات متشابكة ونواقل بعدية كمومية وبوابات تعمل على بتة كمومية واحدة كل مرة. توفر هذه النتيجة طريقة منهجية لبناء بوابات تعمل على بتتين كموميتين. إن الأساس في بناء بوابة بتتين كموميتين من ناقل بعدي هو النقل البعدي لبتتين كموميتين من مدخل البوابة إلى مخرجها باستخدام الأزواج المتشابكة المعدّلة بعناية. تعدَّل الأزواج المتشابكة بطريقة يَستقبل فيها مخرج البوابة البتات الكمومية المعالجة معالجة مناسبة. وهكذا يُختزل إجراء المنطق الكمومي على بتتين كموميتين مجهولتين إلى مهمة تحضير حالات متشابكة معينة سبق تحديدها، يليها النقل البعدي. ومما لا شك فيه أن قياس حالة بِل الكامل، الضروري للنقل البعدي الناجح 100 في المئة، هو نفسه نوع من معالجة البتتين الكموميتين.

إن النقل البعدي الكمومي هو سليل مباشر للسيناريوهات التي تَجادل حولها آينشتاين وبور. فلدى تحليل التجربة سيقودنا تساؤلنا حول الخواص الحقيقية للجسيمات المفردة حين تكون متشابكة إلى مختلف أنواع المشكلات. وينبغي لنا أن نحلل بعناية ماذا يعني "امتلاك" استقطاب. إننا لا نستطيع التهرب من استخلاص ما يلي: إن كل ما بوسعنا الحديث عنه هو نتائج تجريبية معينة حصلنا عليها نتيجة لقياسات. ففي قياسنا الاستقطاب تجعلنا "تكّة" click صادرة عن المكشاف نبني صورة في أذهاننا "يمتلك" فيها الفوتون بالفعل استقطابا معينا لحظة القياس. ومع ذلك يجب أن يبقى ماثل في أذهاننا أن هذه ليست سوى قصة جرى تأليفها made-up، لا تصلح إلا حين نتحدث عن تلك التجربة بالذات، كما يجب أن نكون حذرين لدى استخدامها في ظروف أخرى.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Further details

The proposed channel Φ can be described more explicitly. To begin teleportation, Alice performs a local measurement on the two subsystems (1 and 2) in her possession. Assume the local measurement have effects

${F_{i}}={M_{i}^{2}}.$

If the measurement registers the i-th outcome, the overall state collapses to

$(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I).$

The tensor factor in $(M_{i}\otimes I)$ is $12\otimes 3$ while that of $\rho \otimes \omega$ is $1\otimes 23$. Bob then applies a corresponding local operation Ψ_i on system 3. On the combined system, this is described by

$(Id\otimes \Psi _{i})(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I).$

where Id is the identity map on the composite system $1\otimes 2$.

Therefore the channel Φ is defined by

$\Phi (\rho \otimes \omega )=\sum _{i}(Id\otimes \Psi _{i})(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I)$

Notice Φ satisfies the definition of LOCC. As stated above, the teleportation is said to be successful if, for all observable O on Bob's system, the equality

$\langle \Phi (\rho \otimes \omega ),I\otimes O\rangle =\langle \rho ,O\rangle$

holds. The left hand side of the equation is:

$\sum _{i}\langle (Id\otimes \Psi _{i})(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I),\;I\otimes O\rangle$

$=\sum _{i}\langle (M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I),\;I\otimes \Psi _{i}^{*}(O)\rangle$

where Ψ_i* is the adjoint of Ψ_i in the Heisenberg picture. Assuming all objects are finite dimensional, this becomes

$\sum _{i}\operatorname {Tr} \;(\rho \otimes \omega )(F_{i}\otimes \Psi _{i}^{*}(O)).$

The success criterion for teleportation has the expression

$\sum _{i}\operatorname {Tr} \;(\rho \otimes \omega )(F_{i}\otimes \Psi _{i}^{*}(O))=\operatorname {Tr} \;\rho \cdot O.$

 انظر أيضاً

• Quantum mechanics
  • Introduction to quantum mechanics
  • Quantum nonlocality
  • Quantum computers
  • Quantum entanglement
  • Heisenberg uncertainly principle
  • Quantum energy teleportation

 المصادر

• http://www.oloommagazine.com/Articles/ArticleDetails.aspx?ID=1422

 وصلات خارجية

• signandsight.com:"Spooky action and beyond" - Interview with Prof. Dr. Anton Zeilinger about quantum teleportation. Date: 2006-02-16
• Quantum Teleportation at IBM
• Physicists Succeed In Transferring Information Between Matter And Light
• Quantum telecloning: Captain Kirk's clone and the eavesdropper
• Teleportation-based approaches to universal quantum computation
• Teleportation as a quantum computation
• Quantum teleportation with atoms: quantum process tomography
• Entangled State Teleportation
• Fidelity of quantum teleportation through noisy channels by
• TelePOVM— A generalized quantum teleportation scheme
• Entanglement Teleportation via Werner States
• Quantum Teleportation of a Polarization State
• The Time Travel Handbook: A Manual of Practical Teleportation & Time Travel
• letters to nature: Deterministic quantum teleportation with atoms
• Quantum teleportation with a complete Bell state measurement
• Welcome to the quantum Internet. Science News, Aug. 16 2008.
• Quantum experiments - interactive.
• “A (mostly serious) introduction to quantum teleportation for non-physicists”