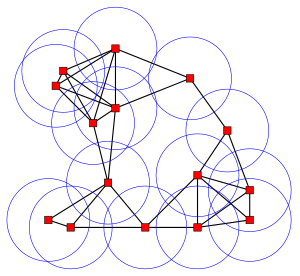
هندسة متقطعة
الهندسة المتقطعة Discrete geometry أو الهندسة التباديلية Combinatorial geometry هو فرع الهندسة الرياضية الذي يدرس الأجسام وخصائصها في الفضاء المتقطع. وهي دراسة لا تعتمد على افتراض استمرارية الأجسام.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تطبيقات الهندسة المتقطعة
للهندسة المتقطعة تطبيقات عديدة في الهندسة الرياضية الرقمية، الهندسة الرياضية الحاسوبية، الهندسة المنتهية وغيرها.
الصلابة والمرونة البنيوية
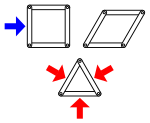
الصلابة البنيوية Structural rigidity هي نظرية توافيق لتوقع مرونة تجميعات مشكـّلة من rigid bodies connected by flexible linkages or hinges.
الموضوعات في هذا المجال تضم:
بنى السقوط
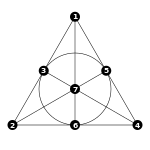
Incidence structures generalize planes (such as affine, projective، و مستويات موبيوس) as can be seen from their axiomatic definitions. Incidence structures also generalize the higher-dimensional analogs and the finite structures are sometimes called finite geometries.
شكلياً، بنية السقوط هو الثلاثي
حيث P is a set of "points", L is a set of "lines" and هي علاقة incidence. عناصر تسمى أعلام. إذا
we say that point p "lies on" line .
الموضوعات في هذا المجال تضم:
مواضيع الهندسة المتقطعة
انظر أيضاً
الهامش
المراجع
- Bezdek, András, (2003). Discrete geometry: in honor of W. Kuperberg's 60th birthday. New York, N.Y: Marcel Dekker. ISBN 0-8247-0968-3.
{{cite book}}: CS1 maint: extra punctuation (link) CS1 maint: multiple names: authors list (link) - Bezdek, Károly (2010). Classical Topics in Discrete Geometry. New York, N.Y: Springer. ISBN 978-1-4419-0599-4.
- Bezdek, Károly (2013). Lectures on Sphere Arrangements - the Discrete Geometric Side. New York, N.Y: Springer. ISBN 978-1-4614-8117-1.
- Bezdek, Károly; Deza, Antoine; Ye, Yinyu (2013). Discrete Geometry and Optimization. New York, N.Y: Springer. ISBN 978-3-319-00200-2.
- Brass, Peter; Moser, William; Pach, János (2005). Research problems in discrete geometry. Berlin: Springer. ISBN 0-387-23815-8.
- Pach, János; Agarwal, Pankaj K. (1995). Combinatorial geometry. New York: Wiley-Interscience. ISBN 0-471-58890-3.
- Goodman, Jacob E. and O'Rourke, Joseph (2004). Handbook of Discrete and Computational Geometry, Second Edition. Boca Raton: Chapman & Hall/CRC. ISBN 1-58488-301-4.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Gruber, Peter M. (2007). Convex and Discrete Geometry. Berlin: Springer. ISBN 3-540-71132-5.
- Matoušek, Jiří (2002). Lectures on discrete geometry. Berlin: Springer. ISBN 0-387-95374-4.
- Vladimir Boltyanski, Horst Martini, Petru S. Soltan, (1997). Excursions into Combinatorial Geometry. Springer. ISBN 3-540-61341-2.
{{cite book}}: Cite has empty unknown parameter:|1=(help)CS1 maint: extra punctuation (link) CS1 maint: multiple names: authors list (link)