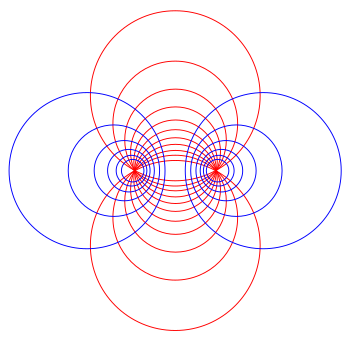
دوائر أپولونية Apollonian circles
في الهندسة الرياضية، تعرف الدوائر الأپولونية إنگليزية: Apollonian circles على أنها مجموعتين من الدوائر بجيث تتقاطع كل دائرة من المجموعة الأولى مع كل دائرة في المجموعة الثانية بشكل متعامد (زاوية قائمة). وتشكل هذه الدوائر أساس لنظام الإحداثيات القطبية الثنائية. تم اكتشاف هذه الدوائر من قبل أپولونيوس من پرگا الإغريقي.
تعريف
تعرف مجموعات الدوائر الأبولونية بطريقتين مختلفتين بواسطة قطعة خط مستقيم تسمى CD.
كل دائرة في العائلة الأولى (الدوائر الزرقاء في الشكل المرفق) تقترن برقم حقيقي موجب r، ويُعرَّف بأنه محل هندسي للنقاط X بحيث أن نسبة المسافات من X إلى C وإلى D تساوي r،
كل دائرة في العائلة الثانية (الدوائر الحمراء في الشكل) مرتبطة بزاوية θ، ومُعرَّفة كمحل هندسي للنقاط X بحيث أن الزاوية المحيطية ∠CXD تساوي θ،
مسح θ من 0 إلى π يولِّد فئة كل الدوائر المارة عبر النقطتين C و D.
النقطتان حيث تكون كل نقاط الدوائر الحمراء تكون نقاط حدية لأزواج الدوائر في العائلة الزرقاء.
الإحداثيات ثنائية القطب
إذا أُعطينا دائرة زرقاء وأخرى حمراء تتقاطعان في نقطتين. للحصول على إحادثيات ثنائية القطب، فإننا نحتاج طريقة لتحديد أي النقطتين هي اليمنى. القوس متعامد المماسات هو المحل الهندسي للنقاط X الني ترى النقاط C, D تحت زاوية معطاة للمتجهات، أي:
حزمة الدوائر
كلتا العائلتين من الدوائر الأپولونية هي حـِزَم دوائر. كل عائلة يحددها أي اثنين من أعضائها، ويُسمَّوْن مولدات الحزمة. وتحديداً، إحداهم هي الحزمة الناقصية (العائلة الحمراء من الدوائر في الشكل المرافق) المُعرَّفة بمولدَين يمران عبر بعضهما البعض بالضبط في نقطتين محددتين (C, D). والأخرى هي الحزمة الزائدية (العائلة الزرقاء من الدوائر في الشكل) المُعرَّفة بمولدَين لا يتقاطعان في أي نقطة.[1]
المحور الأساسي والخط المركزي
أي دائرتين من هذه الدوائر داخل حزمة يكون لهما نفس المحور الأساسي، وجميع الدوائر في الحزمة لهم مراكز متسامتة collinear. أي ثلاث دوائر أو أكثر من نفس العائلة تسمى دوائر محورية coaxial circles.[2]
الحزمة الناقصية من الدوائر المارة في النقطتين C, D (فئة الدوائر الحمراء، في الشكل) يكون لها الخط CD كمحورها الأساسي. مراكز الدوائر في هذه الحزمة تقع على المُنصِّف العمودي للخط CD. الحزمة الزائدية المُعرَّفة بالنقاط C, D (الدوائر الزرقاء) يكون محورها الأساسي على المُنصِّف العمودي للخط CD، وكل مراكز دوائرها على الخط CD.
الهندسة العكسية والتقاطعات المتعامدة وأنظمة الإحداثيات
عكس الدائرة يحوّل المستوى بطريقة تـُرسِل الدوائر إلى دوائر، وحزم الدوائر إلى حزم دوائر. نوع الحزمة يظل محفوظاً: تعاكـُس الحزمة الناقصية هو حزمة ناقصية أخرى، وتعاكُس الحزمة الزائدية هو حزمة زائدية أخرى، وتعاكُس الحزمة المكافئية هو حزمة مكافئية أخرى.
ومن السهولة بمكان أن نبيّن باستخدام التعاكُس أنه، في الدوائر الأبولونية، كل دائرة زرقاء تقطع كل دائرة حمراء تعامدياً، أي على زاوية قائمة. فتعاكُس الدوائر الأبولونية الزرقاء بالنسبة لدائرة مركزها في النقطة C يسفر عن حزمة من الدوائر متحدة المركز عند صورة النقطة D. نفس التعاكس يحوّل الدوائر الحمراء إلى فئة من الخطوط المستقيمة تضم كلها صورة D. لذلك، فهذ التعاكس يحوّل نظام الإحداثيات ثنائية القطب المُعرَّف بدوائر أبولونية إلى نظام إحداثيات قطبية. من الواضح أن حِزَم الدوائر تلتقي على زاوية قائمة. ولما كان التعاكس هو تحويل شكلي، فإنه يحافظ على الزوايا بين المنحنيات التي تحوّلها، حتى تلتقي الدوائر الأبولونية الأصلية أيضاً على زوايا قائمة.
وبدلاً عن ذلك،[3] فإن الخاصية التعامدية للحزمتين تنبع من الخاصية التعريفية للمحور الأساسي، بأنه من أي نقطة X على المحور الأساسي لحزمة P فإن أطوال المماسات من X إلى كل دائرة في P هي متساوية. ويترتب على ذلك أن الدائرة التي مركزها X وطولها يساوي هذه المماسات تتقاطع مع جميع دوائر P بشكل عمودي. ويمكن تطبيق نفس الإنشاء لكل X على محور الأساسي لـ P، مما يشكل حزمة أخرى من الدوائر المتعامدة مع P.
بشكل أعم، لكل حزمة من الدوائر توجد حزمة فريدة تتكون من دوائر متعامدة على الحزمة الأولى. لو إحدى الحزمتين ناقصية، فإن الحزمة المتعامدة تكون زائدية، والعكس صحيح؛ في هذه الحالة، تشكل الحزمتان فئة من الدوائر الأبولونية. حزمة الدوائر المتعامدة على الحزمة التكافئية هي أيضاً تكافئية؛ وتتكون من دوائر لها نفس نقطة التماس المشتركة ولكن مع خط تماس متعامد عند تلك النقطة.[4]
الفيزياء
ثبت أن المسارات الأپولونية تتبعها في حركتها أنوية الدوامات أو حالات شبه دورانية pseudospin محددة أخرى في بعض الأنظمة الفيزيائية التي تتضمن مجالات تداخلية أو مقترنة، مثل موجات الپولاريتون الفوتونية أو المقترنة.[5] تنشأ المسارات من دوران رابي لكرة بلوخ وإسقاطها مجسم على الفضاء الحقيقي حيث تُجرى الأرصاد.
انظر أيضاً
الهامش
- ^ Schwerdtfeger (1962, pp. 8–10).
- ^ MathWorld uses “coaxal,” while Akopyan & Zaslavsky (2007) prefer “coaxial.”
- ^ Akopyan & Zaslavsky (2007), p. 59.
- ^ Schwerdtfeger (1962, pp. 30–31, Theorem A).
- ^ Dominici; et al. (2021), "Full-Bloch beams and ultrafast Rabi-rotating vortices", Physical Review Research, 3 (1): 013007, arXiv:1801.02580, Bibcode:2021PhRvR...3a3007D, doi:10.1103/PhysRevResearch.3.013007
المراجع
- Akopyan, A. V.; Zaslavsky, A. A. (2007), Geometry of Conics, Mathematical World, 26, American Mathematical Society, pp. 57–62, ISBN 978-0-8218-4323-9.
- Pfeifer, Richard E.; Van Hook, Cathleen (1993), "Circles, Vectors, and Linear Algebra", Mathematics Magazine 66 (2): 75–86, doi:.
- Schwerdtfeger, Hans (1979), Geometry of Complex Numbers: Circle Geometry, Moebius Transformation, Non-Euclidean Geometry, Dover, pp. 8–10.
- Samuel, Pierre (1988), Projective Geometry, Springer, pp. 40–43.
- Ogilvy, C. Stanley (1990), Excursions in Geometry, Dover, ISBN 0-486-26530-7, https://archive.org/details/excursionsingeom0000ogil.
وصلات خارجية
- Eric W. Weisstein, Coaxal Circles at MathWorld.
- David B. Surowski: Advanced High-School Mathematics. p. 31