إسقاط مجسم Stereographic projection
 |
| جزء من سلسلة عن: |
| الإسقاط الهندسي |
|---|
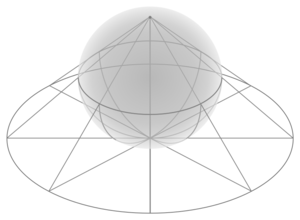
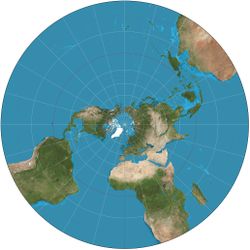
في الهندسة، الإسقاط المجسم stereographic projection، هو تخطيط دالة معينة تعكس كرة ما على مستوى. يُعين الإسقاط على الكرة بأكملها، عدا نقطة واحدة: نقطة الإسقاط. عند تعيينها، تكون الدالة ناعمة وتقابلية. يكون الإسقاط المجسم تشكيلياً، مما يعني أنه يحافظ على زوايا التقاء المنحيات. لا يكون الإسقاط المجسم تقايسياً] ولا محافظاً على المساحة: فهو لا يحافظ على المسافات ولا على مساحات الأشكال.
بديهياً، يعتبر الإسقاط المجسم طريقة لتصوير الكرة كمستوى، مع بعض المقاربات التي لا بد منها. لأن الكرة والمستوى يظهران في الكثير من مجالات الرياضيات وتطبيقاتها، لذلك، يستخدم الإسقاط المجسم في مختلف المجالات ومنها التحليل المركب، رسم الخرائط، الجيولوجيا، والتصوير الفوتوغرافي. عملياً، يتم تنفيذ الإسقاط عن طريق الحاسوب أو يدوياً باستخدام نوع معين من ورق الرسم البياني يسمى شبكة التجسيم أو شبكة وولف.
Intuitively, the stereographic projection is a way of picturing the sphere as the plane, with some inevitable compromises. Because the sphere and the plane appear in many areas of mathematics and its applications, so does the stereographic projection; it finds use in diverse fields including complex analysis, cartography, geology, and photography. Sometimes stereographic computations are done graphically using a special kind of graph paper called a stereographic net, shortened to stereonet, or Wulff net.
التاريخ

The origin of the stereographic projection is not known, but it is believed to have been discovered by Ancient Greek astronomers and used for projecting the celestial sphere to the plane so that the motions of stars and planets could be analyzed using plane geometry. Its earliest extant description is found in Ptolemy's Planisphere (2nd century AD), but it was ambiguously attributed to Hipparchus (2nd century BC) by Synesius (ح. 400 AD),[1] and Apollonius's Conics (ح. 200 BC) contains a theorem which is crucial in proving the property that the stereographic projection maps circles to circles. Hipparchus, Apollonius, Archimedes, and even Eudoxus (4th century BC) have sometimes been speculatively credited with inventing or knowing of the stereographic projection,[2] but some experts consider these attributions unjustified.[1] Ptolemy refers to the use of the stereographic projection in a "horoscopic instrument", perhaps the anaphoric clock described by Vitruvius (1st century BC).[3][4]
By the time of Theon of Alexandria (4th century), the planisphere had been combined with a dioptra to form the planispheric astrolabe ("star taker"),[2] a capable portable device which could be used for measuring star positions and performing a wide variety of astronomical calculations. The astrolabe was in continuous use by Byzantine astronomers, and was significantly further developed by medieval Islamic astronomers. It was transmitted to Western Europe during the 11th–12th century, with Arabic texts translated into Latin.
In the 16th and 17th century, the equatorial aspect of the stereographic projection was commonly used for maps of the Eastern and Western Hemispheres. It is believed that already the map created in 1507 by Gualterius Lud[5] was in stereographic projection, as were later the maps of Jean Rotz (1542), Rumold Mercator (1595), and many others.[6] In star charts, even this equatorial aspect had been utilised already by the ancient astronomers like Ptolemy.[7]
François d'Aguilon gave the stereographic projection its current name in his 1613 work Opticorum libri sex philosophis juxta ac mathematicis utiles (Six Books of Optics, useful for philosophers and mathematicians alike).[8]
In the late 16th century, Thomas Harriot proved that the stereographic projection is conformal; however, this proof was never published and sat among his papers in a box for more than three centuries.[9] In 1695, Edmond Halley, motivated by his interest in star charts, was the first to publish a proof.[10] He used the recently established tools of calculus, invented by his friend Isaac Newton.
التعريف
الصيغة الأولى

The unit sphere in three-dimensional space is the set of points such that . Let be the "north pole", and let be the rest of the sphere. The plane runs through the center of the sphere; the "equator" is the intersection of the sphere with this plane.
For any point on , there is a unique line through and , and this line intersects the plane in exactly one point , known as the stereographic projection of onto the plane.
In Cartesian coordinates on the sphere and on the plane, the projection and its inverse are given by the formulas
In spherical coordinates on the sphere (with the zenith angle, , and the azimuth, ) and polar coordinates on the plane, the projection and its inverse are
Here, is understood to have value when . Also, there are many ways to rewrite these formulas using trigonometric identities. In cylindrical coordinates on the sphere and polar coordinates on the plane, the projection and its inverse are
تعريفات أخرى
Some authors[11] define stereographic projection from the north pole (0, 0, 1) onto the plane z = −1, which is tangent to the unit sphere at the south pole (0, 0, −1). This can be described as a composition of a projection onto the equatorial plane described above, and a homothety from it to the polar plane. The homothety scales the image by a factor of 2 (a ratio of a diameter to a radius of the sphere), hence the values X and Y produced by this projection are exactly twice those produced by the equatorial projection described in the preceding section. For example, this projection sends the equator to the circle of radius 2 centered at the origin. While the equatorial projection produces no infinitesimal area distortion along the equator, this pole-tangent projection instead produces no infinitesimal area distortion at the south pole.
Other authors[12] use a sphere of radius 1/2 and the plane z = −1/2. In this case the formulae become
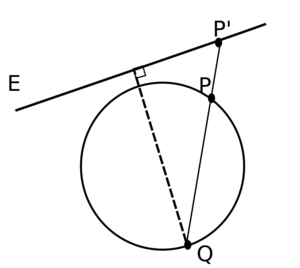
In general, one can define a stereographic projection from any point Q on the sphere onto any plane E such that
- E is perpendicular to the diameter through Q, and
- E does not contain Q.
As long as E meets these conditions, then for any point P other than Q the line through P and Q meets E in exactly one point P′, which is defined to be the stereographic projection of P onto E.[13]
تعميمات
More generally, stereographic projection may be applied to the unit n-sphere Sn in (n + 1)-dimensional Euclidean space En+1. If Q is a point of Sn and E a hyperplane in En+1, then the stereographic projection of a point P ∈ Sn − {Q} is the point P′ of intersection of the line QP with E. In Cartesian coordinates (xi, i from 0 to n) on Sn and (Xi, i from 1 to n) on E, the projection from Q = (1, 0, 0, ..., 0) ∈ Sn is given by
Still more generally, suppose that S is a (nonsingular) quadric hypersurface in the projective space Pn+1. In other words, S is the locus of zeros of a non-singular quadratic form f(x0, ..., xn+1) in the homogeneous coordinates xi. Fix any point Q on S and a hyperplane E in Pn+1 not containing Q. Then the stereographic projection of a point P in S − {Q} is the unique point of intersection of QP with E. As before, the stereographic projection is conformal and invertible on a non-empty Zariski open set. The stereographic projection presents the quadric hypersurface as a rational hypersurface.[14] This construction plays a role in algebraic geometry and conformal geometry.
الخصائص
The first stereographic projection defined in the preceding section sends the "south pole" (0, 0, −1) of the unit sphere to (0, 0), the equator to the unit circle, the southern hemisphere to the region inside the circle, and the northern hemisphere to the region outside the circle.
The projection is not defined at the projection point N = (0, 0, 1). Small neighborhoods of this point are sent to subsets of the plane far away from (0, 0). The closer P is to (0, 0, 1), the more distant its image is from (0, 0) in the plane. For this reason it is common to speak of (0, 0, 1) as mapping to "infinity" in the plane, and of the sphere as completing the plane by adding a point at infinity. This notion finds utility in projective geometry and complex analysis. On a merely topological level, it illustrates how the sphere is homeomorphic to the one-point compactification of the plane.
In Cartesian coordinates a point P(x, y, z) on the sphere and its image P′(X, Y) on the plane either both are rational points or none of them:
Stereographic projection is conformal, meaning that it preserves the angles at which curves cross each other (see figures). On the other hand, stereographic projection does not preserve area; in general, the area of a region of the sphere does not equal the area of its projection onto the plane. The area element is given in (X, Y) coordinates by
Along the unit circle, where X2 + Y2 = 1, there is no inflation of area in the limit, giving a scale factor of 1. Near (0, 0) areas are inflated by a factor of 4, and near infinity areas are inflated by arbitrarily small factors.
The metric is given in (X, Y) coordinates by
and is the unique formula found in Bernhard Riemann's Habilitationsschrift on the foundations of geometry, delivered at Göttingen in 1854, and entitled Über die Hypothesen welche der Geometrie zu Grunde liegen.
No map from the sphere to the plane can be both conformal and area-preserving. If it were, then it would be a local isometry and would preserve Gaussian curvature. The sphere and the plane have different Gaussian curvatures, so this is impossible.
Circles on the sphere that do not pass through the point of projection are projected to circles on the plane.[15][16] Circles on the sphere that do pass through the point of projection are projected to straight lines on the plane. These lines are sometimes thought of as circles through the point at infinity, or circles of infinite radius. These properties can be verified by using the expressions of in terms of given in § First formulation: using these expressions for a substitution in the equation of the plane containing a circle on the sphere, and clearing denominators, one gets the equation of a circle, that is, a second-degree equation with as its quadratic part. The equation becomes linear if that is, if the plane passes through the point of projection.
All lines in the plane, when transformed to circles on the sphere by the inverse of stereographic projection, meet at the projection point. Parallel lines, which do not intersect in the plane, are transformed to circles tangent at projection point. Intersecting lines are transformed to circles that intersect transversally at two points in the sphere, one of which is the projection point. (Similar remarks hold about the real projective plane, but the intersection relationships are different there.)
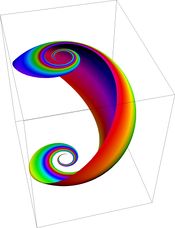
The loxodromes of the sphere map to curves on the plane of the form
where the parameter a measures the "tightness" of the loxodrome. Thus loxodromes correspond to logarithmic spirals. These spirals intersect radial lines in the plane at equal angles, just as the loxodromes intersect meridians on the sphere at equal angles.
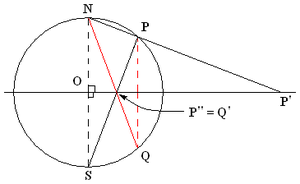
The stereographic projection relates to the plane inversion in a simple way. Let P and Q be two points on the sphere with projections P′ and Q′ on the plane. Then P′ and Q′ are inversive images of each other in the image of the equatorial circle if and only if P and Q are reflections of each other in the equatorial plane.
In other words, if:
- P is a point on the sphere, but not a 'north pole' N and not its antipode, the 'south pole' S,
- P′ is the image of P in a stereographic projection with the projection point N and
- P″ is the image of P in a stereographic projection with the projection point S,
then P′ and P″ are inversive images of each other in the unit circle.
شبكة وولف
Stereographic projection plots can be carried out by a computer using the explicit formulas given above. However, for graphing by hand these formulas are unwieldy. Instead, it is common to use graph paper designed specifically for the task. This special graph paper is called a stereonet or Wulff net, after the Russian mineralogist George (Yuri Viktorovich) Wulff.[17]
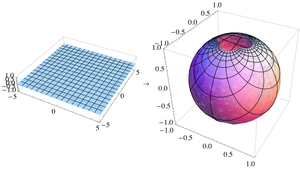
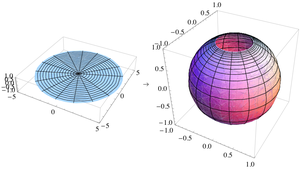
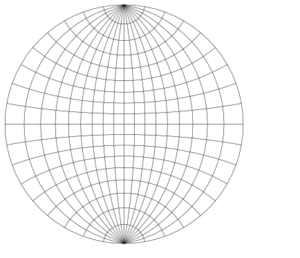
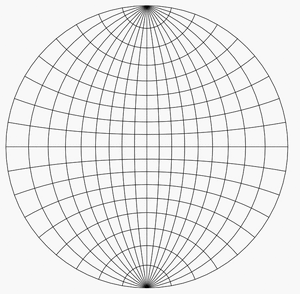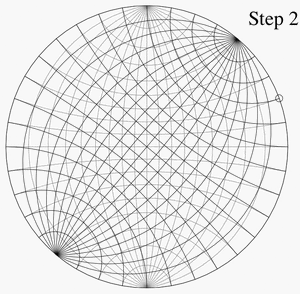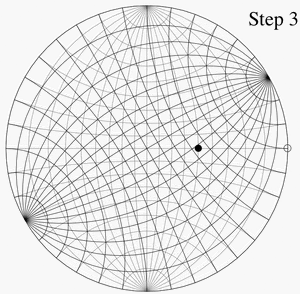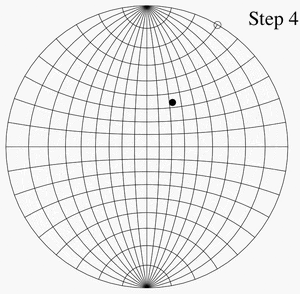
The Wulff net shown here is the stereographic projection of the grid of parallels and meridians of a hemisphere centred at a point on the equator (such as the Eastern or Western hemisphere of a planet).
In the figure, the area-distorting property of the stereographic projection can be seen by comparing a grid sector near the center of the net with one at the far right or left. The two sectors have equal areas on the sphere. On the disk, the latter has nearly four times the area of the former. If the grid is made finer, this ratio approaches exactly 4.
On the Wulff net, the images of the parallels and meridians intersect at right angles. This orthogonality property is a consequence of the angle-preserving property of the stereographic projection. (However, the angle-preserving property is stronger than this property. Not all projections that preserve the orthogonality of parallels and meridians are angle-preserving.)
For an example of the use of the Wulff net, imagine two copies of it on thin paper, one atop the other, aligned and tacked at their mutual center. Let P be the point on the lower unit hemisphere whose spherical coordinates are (140°, 60°) and whose Cartesian coordinates are (0.321, 0.557, −0.766). This point lies on a line oriented 60° counterclockwise from the positive x-axis (or 30° clockwise from the positive y-axis) and 50° below the horizontal plane z = 0. Once these angles are known, there are four steps to plotting P:
- Using the grid lines, which are spaced 10° apart in the figures here, mark the point on the edge of the net that is 60° counterclockwise from the point (1, 0) (or 30° clockwise from the point (0, 1)).
- Rotate the top net until this point is aligned with (1, 0) on the bottom net.
- Using the grid lines on the bottom net, mark the point that is 50° toward the center from that point.
- Rotate the top net oppositely to how it was oriented before, to bring it back into alignment with the bottom net. The point marked in step 3 is then the projection that we wanted.
To plot other points, whose angles are not such round numbers as 60° and 50°, one must visually interpolate between the nearest grid lines. It is helpful to have a net with finer spacing than 10°. Spacings of 2° are common.
To find the central angle between two points on the sphere based on their stereographic plot, overlay the plot on a Wulff net and rotate the plot about the center until the two points lie on or near a meridian. Then measure the angle between them by counting grid lines along that meridian.
تطبيقات في الرياضيات
التحليل المركب

Although any stereographic projection misses one point on the sphere (the projection point), the entire sphere can be mapped using two projections from distinct projection points. In other words, the sphere can be covered by two stereographic parametrizations (the inverses of the projections) from the plane. The parametrizations can be chosen to induce the same orientation on the sphere. Together, they describe the sphere as an oriented surface (or two-dimensional manifold).
This construction has special significance in complex analysis. The point (X, Y) in the real plane can be identified with the complex number ζ = X + iY. The stereographic projection from the north pole onto the equatorial plane is then
Similarly, letting ξ = X − iY be another complex coordinate, the functions
define a stereographic projection from the south pole onto the equatorial plane. The transition maps between the ζ- and ξ-coordinates are then ζ = 1/ξ and ξ = 1/ζ, with ζ approaching 0 as ξ goes to infinity, and vice versa. This facilitates an elegant and useful notion of infinity for the complex numbers and indeed an entire theory of meromorphic functions mapping to the Riemann sphere. The standard metric on the unit sphere agrees with the Fubini–Study metric on the Riemann sphere.
تصور الخطوط والمستويات

The set of all lines through the origin in three-dimensional space forms a space called the real projective plane. This plane is difficult to visualize, because it cannot be embedded in three-dimensional space.
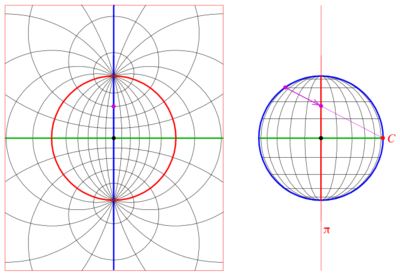
However, one can visualize it as a disk, as follows. Any line through the origin intersects the southern hemisphere z ≤ 0 in a point, which can then be stereographically projected to a point on a disk in the XY plane. Horizontal lines through the origin intersect the southern hemisphere in two antipodal points along the equator, which project to the boundary of the disk. Either of the two projected points can be considered part of the disk; it is understood that antipodal points on the equator represent a single line in 3 space and a single point on the boundary of the projected disk (see quotient topology). So any set of lines through the origin can be pictured as a set of points in the projected disk. But the boundary points behave differently from the boundary points of an ordinary 2-dimensional disk, in that any one of them is simultaneously close to interior points on opposite sides of the disk (just as two nearly horizontal lines through the origin can project to points on opposite sides of the disk).
Also, every plane through the origin intersects the unit sphere in a great circle, called the trace of the plane. This circle maps to a circle under stereographic projection. So the projection lets us visualize planes as circular arcs in the disk. Prior to the availability of computers, stereographic projections with great circles often involved drawing large-radius arcs that required use of a beam compass. Computers now make this task much easier.
Further associated with each plane is a unique line, called the plane's pole, that passes through the origin and is perpendicular to the plane. This line can be plotted as a point on the disk just as any line through the origin can. So the stereographic projection also lets us visualize planes as points in the disk. For plots involving many planes, plotting their poles produces a less-cluttered picture than plotting their traces.
This construction is used to visualize directional data in crystallography and geology, as described below.
تصوير آخر
Stereographic projection is also applied to the visualization of polytopes. In a Schlegel diagram, an n-dimensional polytope in Rn+1 is projected onto an n-dimensional sphere, which is then stereographically projected onto Rn. The reduction from Rn+1 to Rn can make the polytope easier to visualize and understand.
الهندسة الحسابية

In elementary arithmetic geometry, stereographic projection from the unit circle provides a means to describe all primitive Pythagorean triples. Specifically, stereographic projection from the north pole (0,1) onto the x-axis gives a one-to-one correspondence between the rational number points (x, y) on the unit circle (with y ≠ 1) and the rational points of the x-axis. If (m/n, 0) is a rational point on the x-axis, then its inverse stereographic projection is the point
which gives Euclid's formula for a Pythagorean triple.
استبدال نصف زاوية المماس
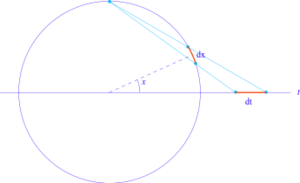
The pair of trigonometric functions (sin x, cos x) can be thought of as parametrizing the unit circle. The stereographic projection gives an alternative parametrization of the unit circle:
Under this reparametrization, the length element dx of the unit circle goes over to
This substitution can sometimes simplify integrals involving trigonometric functions.
تطبيقات في مجالات أخرى
رسم الخرائط
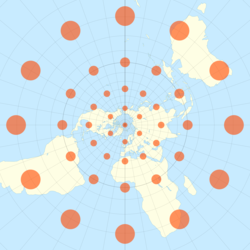
The fundamental problem of cartography is that no map from the sphere to the plane can accurately represent both angles and areas. In general, area-preserving map projections are preferred for statistical applications, while angle-preserving (conformal) map projections are preferred for navigation.
Stereographic projection falls into the second category. When the projection is centered at the Earth's north or south pole, it has additional desirable properties: It sends meridians to rays emanating from the origin and parallels to circles centered at the origin.
The stereographic projection with Tissot's indicatrix of deformation.
Planetary science

The stereographic is the only projection that maps all circles on a sphere to circles on a plane. This property is valuable in planetary mapping where craters are typical features. The set of circles passing through the point of projection have unbounded radius, and therefore degenerate into lines.
علم البلورات
The fundamental problem of cartography is that no map from the sphere to the plane can accurately represent both angles and areas. In general, area-preserving map projections are preferred for statistical applications, while angle-preserving (conformal) map projections are preferred for navigation.
Stereographic projection falls into the second category. When the projection is centered at the Earth's north or south pole, it has additional desirable properties: It sends meridians to rays emanating from the origin and parallels to circles centered at the origin.
The stereographic projection with Tissot's indicatrix of deformation.
Planetary science

The stereographic is the only projection that maps all circles on a sphere to circles on a plane. This property is valuable in planetary mapping where craters are typical features. The set of circles passing through the point of projection have unbounded radius, and therefore degenerate into lines.
الجيولوجيا
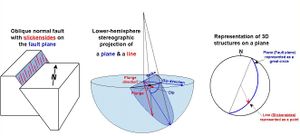
Researchers in structural geology are concerned with the orientations of planes and lines for a number of reasons. The foliation of a rock is a planar feature that often contains a linear feature called lineation. Similarly, a fault plane is a planar feature that may contain linear features such as slickensides.
These orientations of lines and planes at various scales can be plotted using the methods of the Visualization of lines and planes section above. As in crystallography, planes are typically plotted by their poles. Unlike crystallography, the southern hemisphere is used instead of the northern one (because the geological features in question lie below the Earth's surface). In this context the stereographic projection is often referred to as the equal-angle lower-hemisphere projection. The equal-area lower-hemisphere projection defined by the Lambert azimuthal equal-area projection is also used, especially when the plot is to be subjected to subsequent statistical analysis such as density contouring.[18]
Rock mechanics
The stereographic projection is one of the most widely used methods for evaluating rock slope stability. It allows for the representation and analysis of three-dimensional orientation data in two dimensions. Kinematic analysis within stereographic projection is used to assess the potential for various modes of rock slope failures—such as plane, wedge, and toppling failures—which occur due to the presence of unfavorably oriented discontinuities.[19][20] This technique is particularly useful for visualizing the orientation of rock slopes in relation to discontinuity sets, facilitating the assessment of the most likely failure type.[19] For instance, plane failure is more likely when the strike of a discontinuity set is parallel to the slope, and the discontinuities dip towards the slope at an angle steep enough to allow sliding, but not steeper than the slope itself.
Additionally, some authors have developed graphical methods based on stereographic projection to easily calculate geometrical correction parameters—such as those related to the parallelism between the slope and discontinuities, the dip of the discontinuity, and the relative angle between the discontinuity and the slope—for rock mass classifications in slopes, including slope mass rating (SMR)[21] and rock mass rating.[22]
التصوير الفوتوغرافي

Some fisheye lenses use a stereographic projection to capture a wide-angle view.[23] Compared to more traditional fisheye lenses which use an equal-area projection, areas close to the edge retain their shape, and straight lines are less curved. However, stereographic fisheye lenses are typically more expensive to manufacture.[24] Image remapping software, such as Panotools, allows the automatic remapping of photos from an equal-area fisheye to a stereographic projection.
The stereographic projection has been used to map spherical panoramas, starting with Horace Bénédict de Saussure's in 1779. This results in effects known as a little planet (when the center of projection is the nadir) and a tube (when the center of projection is the zenith).[25]
The popularity of using stereographic projections to map panoramas over other azimuthal projections is attributed to the shape preservation that results from the conformality of the projection.[25]
انظر أيضاً
المصادر
- ^ أ ب Synesius wrote in a letter describing an instrument involving the stereographic projection: "Hipparchus long ago hinted at the unfolding of a spherical surface [on a plane], so as to keep a proper proportion between the given ratios in the different figures, and he was in fact the first to apply himself to this subject. I, however (if it is not presumptuous to make so great a claim), have followed it to its uttermost conclusion, and have perfected it, although for most of the intervening time the problem had been neglected; for the great Ptolemy and the divine band of his successors were content to make only such use of it as sufficed for the night-clock by means of the sixteen stars, which were the only ones that Hipparchus rearranged and entered on his instrument." Translation from Dicks, D.R. (1960). The Geographical Fragments of Hipparchus. University of London, Athlone Press, fragment 63 pp. 102–103. Dicks concludes (commentary on fragment 63, pp. 194–207): "Whether Synesius' evidence can be accepted at its face value depends on the view taken as to the strength of the objections raised above. On the whole, it would seem that the value of his testimony has been greatly exaggerated, and its unsatisfactory nature on so many points insufficiently emphasized. At any rate, the 'instrument' he sent to Paeonius was either a modified astrolabic clock of the Vitruvian type or a simple celestial map, and not a planispheric astrolabe. Furthermore, on the evidence available we are not, in my opinion, justified in attributing to Hipparchus a knowledge of either stereographic projection or the planispheric astrolabe."
- ^ أ ب Neugebauer, Otto (1949). "The Early History of the Astrolabe". Isis. 40 (3): 240–256. doi:10.1086/349045. JSTOR 227240.
- ^ Sleeswyk, A.W.; Huldén, B. (1991). "The three waterclocks described by Vitruvius". History and Technology. 8 (1): 25–50. doi:10.1080/07341519108581788.
- ^ Drachmann, A.G . (1953). "The Plane Astrolabe and the Anaphoric Clock". Centaurus. 3 (1): 183–189. Bibcode:1953Cent....3..183D. doi:10.1111/j.1600-0498.1953.tb00528.x.
- ^ According to (Snyder 1993), although he acknowledges he did not personally see it
- ^ Snyder (1989).
- ^ Brown, Lloyd Arnold : The story of maps, p.59.
- ^ According to (Elkins, 1988) who references Eckert, "Die Kartenwissenschaft", Berlin 1921, pp 121–123
- ^ Lohne, John (1979). "Essays on Thomas Harriot". Archive for History of Exact Sciences. 20 (3/4): 189–312. doi:10.1007/BF00327737. S2CID 118095486.
- ^ Timothy Feeman. 2002. "Portraits of the Earth: A Mathematician Looks at Maps". American Mathematical Society.
- ^ Cf. Apostol (1974) p. 17.
- ^ Gelfand, Minlos & Shapiro 1963
- ^ Cf. Pedoe (1988).
- ^ Cf. Shafarevich (1995).
- ^ Ahlfors, Lars (1966). Complex Analysis. McGraw-Hill, Inc. p. 19.
- ^ Conway, John; Doyle, Peter; Gilman, Jane; Thurston, Bill (1994-04-12), "Stereographic Projection", Geometry and the Imagination in Minneapolis, Minnesota University, http://www.geom.uiuc.edu/docs/doyle/mpls/handouts/node33.html, retrieved on 2022-04-26
- ^ Wulff, George, Untersuchungen im Gebiete der optischen Eigenschaften isomorpher Kristalle: Zeits. Krist.,36, 1–28 (1902)
- ^ Lisle, R.J.; Leyshon, P.R. (2004). Stereographic Projection Techniques for Geologists and Civil Engineers (2 ed.). Cambridge University Press. ISBN 9780521535823.
- ^ أ ب Hoek, Evert; Bray, Jonathan D. (1981-06-30). Rock Slope Engineering: Third Edition. CRC Press. ISBN 978-0-419-16010-6.
- ^ Lisle, Richard J.; Leyshon, Peter R. (2004). Stereographic Projection Techniques for Geologists and Civil Engineers (2 ed.). Cambridge: Cambridge University Press. doi:10.1017/cbo9781139171366. ISBN 978-0-521-53582-3.
- ^ Tomás, R.; Cuenca, A.; Cano, M.; García-Barba, J. (2012-01-04). "A graphical approach for slope mass rating (SMR)". Engineering Geology. 124: 67–76. Bibcode:2012EngGe.124...67T. doi:10.1016/j.enggeo.2011.10.004. ISSN 0013-7952.
- ^ Moon, Vicki; Russell, Geoff; Stewart, Meagan (July 2001). "The value of rock mass classification systems for weak rock masses: a case example from Huntly, New Zealand". Engineering Geology. 61 (1): 53–67. Bibcode:2001EngGe..61...53M. doi:10.1016/s0013-7952(01)00024-2. ISSN 0013-7952.
- ^ Samyang 8 mm f/3.5 Fisheye CS Archived 2011-06-29 at the Wayback Machine
- ^ "Samyang 8 mm f/3.5 Aspherical IF MC Fish-eye". lenstip.com. Retrieved 2011-07-07.
- ^ أ ب German et al. (2007).
المراجع
- Apostol, Tom (1974). Mathematical Analysis (2 ed.). Addison-Wesley. ISBN 0-201-00288-4.
- Brown, James; Churchill, Ruel (1989). Complex variables and applications. New York: McGraw-Hill. ISBN 0-07-010905-2.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - Casselman, Bill (2014), Feature column February 2014:Stereographic Projection, AMS, http://www.ams.org/samplings/feature-column/fc-2014-02, retrieved on 2014-12-12
- German, Daniel (June 2007). "Flattening the Viewable Sphere". "Proceedings of Computational Aesthetics 2007": 23–28, Banff: Eurographics.
- Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation and Lorentz Groups and their Applications, New York: Pergamon Press
- Do Carmo; Manfredo P. (1976). Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-212589-7.
- Elkins, James (1988). "Did Leonardo Develop a Theory of Curvilinear Perspective?: Together with Some Remarks on the 'Angle' and 'Distance' Axioms". Journal of the Warburg and Courtauld Institutes. The Warburg Institute. 51: 190–196. doi:10.2307/751275. JSTOR 751275.
- Oprea, John (2003). Differential geometry and applications. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-065246-6.
- Pedoe, Dan (1988). Geometry. Dover. ISBN 0-486-65812-0.
- Shafarevich, Igor (1995). Basic Algebraic Geometry I. Springer. ISBN 0-387-54812-2.
- Snyder, John P. (1987). Map Projections − A Working Manual, Professional Paper 1395. US Geological Survey.
- Snyder, John P. (1989). An Album of Map Projections, Professional Paper 1453. US Geological Survey.
- Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
- Spivak, Michael (1999). A comprehensive introduction to differential geometry, Volume IV. Houston, Texas: Publish or Perish. ISBN 0-914098-73-X.
وصلات خارجية
- Eric W. Weisstein, Stereographic projection at MathWorld.
- Stereographic Projection on PlanetMath
- Stereographic Projection and Inversion from Cut-the-Knot
- DoITPoMS Teaching and Learning Package - "The Stereographic Projection"
مرئيات
- Proof about Stereographic Projection taking circles in the sphere to circles in the plane
- Time Lapse Stereographic Projection on Vimeo
برمجيات
- Free and open source python program for stereographic projection - PTCLab
- Sphaerica software is capable of displaying spherical constructions in stereographic projection
- Three dimensional Java Applet