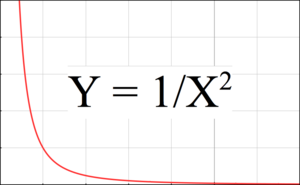بروز مدي

البروز المدي Tidal force هو حدوث ركامين مائيين من بحار الكرة الأرضية يحدثان بفعل قوة جاذبية الشمس والقمر. وطالما تدور الكرة الأرضية حول محورها كل يوم فهذان البروزان يتحركان فوق سطح الارض وينتجان المد والجزر .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الشرح

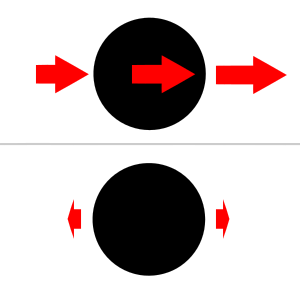
When a body (body 1) is acted on by the gravity of another body (body 2), the field can vary significantly on body 1 between the side of the body facing body 2 and the side facing away from body 2. Figure 4 shows the differential force of gravity on a spherical body (body 1) exerted by another body (body 2). These so-called tidal forces cause strains on both bodies and may distort them or even, in extreme cases, break one or the other apart.[1] The Roche limit is the distance from a planet at which tidal effects would cause an object to disintegrate because the differential force of gravity from the planet overcomes the attraction of the parts of the object for one another.[2] These strains would not occur if the gravitational field were uniform, because a uniform field only causes the entire body to accelerate together in the same direction and at the same rate.
Size and distance
The relationship of an astronomical body's size, to its distance from another body, strongly influences the magnitude of tidal force.[3] The tidal force acting on an astronomical body, such as the Earth, is directly proportional to the diameter of that astronomical body and inversely proportional to the cube of the distance from another body producing a gravitational attraction, such as the Moon or the Sun. Tidal action on bath tubs, swimming pools, lakes, and other small bodies of water is negligible.[4]
Figure 3 is a graph showing how gravitational force declines with distance. In this graph, the attractive force decreases in proportion to the square of the distance, while the slope relative to value decreases in direct proportion to the distance. This is why the gradient or tidal force at any point is inversely proportional to the cube of the distance.
The tidal force corresponds to the difference in Y between two points on the graph, with one point on the near side of the body, and the other point on the far side. The tidal force becomes larger, when the two points are either farther apart, or when they are more to the left on the graph, meaning closer to the attracting body.
For example, the Moon produces a greater tidal force on the Earth than the Sun, even though the Sun exerts a greater gravitational attraction on the Earth than the Moon, because the gradient is less.
Gravitational attraction is inversely proportional to the square of the distance from the source. The attraction will be stronger on the side of a body facing the source, and weaker on the side away from the source. The tidal force is proportional to the difference.[4]
Sun, Earth, and Moon
As expected, the table below shows that the distance from the Moon to the Earth, is the same as the distance from the Earth to the Moon. The Earth is 81 times more massive than the Moon but has roughly 4 times its radius. As a result, at the same distance, the tidal force of the Earth at the surface of the Moon is about 20 times stronger than that of the Moon at the Earth's surface.[5]
| Gravitational body causing tidal force | Body subjected to tidal force | Diameter and distance | Tidal force | |||
|---|---|---|---|---|---|---|
| Body | Mass (m) | Body | Radius (r) | Distance (d) | ||
| Sun | 1.99×1030 kg | Earth | 6.37×106 m | 1.50×1011 m | 3.81×10−27 m−2 | 5.05×10−7 m⋅s−2 |
| Moon | 7.34×1022 kg | Earth | 6.37×106 m | 3.84×108 m | 2.24×10−19 m−2 | 1.10×10−6 m⋅s−2 |
| Earth | 5.97×1024 kg | Moon | 1.74×106 m | 3.84×108 m | 6.12×10−20 m−2 | 2.44×10−5 m⋅s−2 |
| m is mass; r is radius; d is distance; 2r is the diameter
G is the gravitational constant = 6.674×10−11 m3 kg−1 s−2[6] | ||||||
آثار قوى المد والجزر
الصياغة الرياضية
By Newton's law of universal gravitation and laws of motion, a body of mass m at distance R from the center of a sphere of mass M feels a force ,
equivalent to an acceleration ,
where is a unit vector pointing from the body M to the body m (here, acceleration from m towards M has negative sign).
Consider now the acceleration due to the sphere of mass M experienced by a particle in the vicinity of the body of mass m. With R as the distance from the center of M to the center of m, let ∆r be the (relatively small) distance of the particle from the center of the body of mass m. For simplicity, distances are first considered only in the direction pointing towards or away from the sphere of mass M. If the body of mass m is itself a sphere of radius ∆r, then the new particle considered may be located on its surface, at a distance (R ± ∆r) from the centre of the sphere of mass M, and ∆r may be taken as positive where the particle's distance from M is greater than R. Leaving aside whatever gravitational acceleration may be experienced by the particle towards m on account of m's own mass, we have the acceleration on the particle due to gravitational force towards M as:
Pulling out the R2 term from the denominator gives:
The Maclaurin series of is which gives a series expansion of:
The first term is the gravitational acceleration due to M at the center of the reference body , i.e., at the point where is zero. This term does not affect the observed acceleration of particles on the surface of m because with respect to M, m (and everything on its surface) is in free fall. When the force on the far particle is subtracted from the force on the near particle, this first term cancels, as do all other even-order terms. The remaining (residual) terms represent the difference mentioned above and are tidal force (acceleration) terms. When ∆r is small compared to R, the terms after the first residual term are very small and can be neglected, giving the approximate tidal acceleration for the distances ∆r considered, along the axis joining the centers of m and M:
When calculated in this way for the case where ∆r is a distance along the axis joining the centers of m and M, is directed outwards from to the center of m (where ∆r is zero).
Tidal accelerations can also be calculated away from the axis connecting the bodies m and M, requiring a vector calculation. In the plane perpendicular to that axis, the tidal acceleration is directed inwards (towards the center where ∆r is zero), and its magnitude is in linear approximation as in Figure 4.
The tidal accelerations at the surfaces of planets in the Solar System are generally very small. For example, the lunar tidal acceleration at the Earth's surface along the Moon–Earth axis is about 1.1×10−7 g, while the solar tidal acceleration at the Earth's surface along the Sun–Earth axis is about 0.52×10−7 g, where g is the gravitational acceleration at the Earth's surface. Hence the tide-raising force (acceleration) due to the Sun is about 45% of that due to the Moon.[9] The solar tidal acceleration at the Earth's surface was first given by Newton in the Principia.[10]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
انظر أيضا
- المد والجزر
- جاذبية
- Amphidromic point
- Disrupted planet
- Galactic tide
- Tidal resonance
- Tidal stripping
- Tidal tensor
- Spacetime curvature
المصادر
- مؤمن, عبد الأمير (2006). قاموس دار العلم الفلكي. بيروت، لبنان: دار العلم للملايين.
{{cite book}}: Cite has empty unknown parameter:|طبعة أولى coauthors=(help)
- ^
R Penrose (1999). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press. p. 264. ISBN 978-0-19-286198-6.
tidal force.
- ^ Thérèse Encrenaz; J -P Bibring; M Blanc (2003). The Solar System. Springer. p. 16. ISBN 978-3-540-00241-3.
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةTyson - ^ أ ب Sawicki, Mikolaj (1999). "Myths about gravity and tides". The Physics Teacher. 37 (7): 438–441. Bibcode:1999PhTea..37..438S. CiteSeerX 10.1.1.695.8981. doi:10.1119/1.880345. ISSN 0031-921X.
- ^ Schutz, Bernard (2003). Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity (illustrated ed.). Cambridge University Press. p. 45. ISBN 978-0-521-45506-0. Extract of page 45
- ^ "CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2011. Retrieved 2011-06-23.
{{cite web}}: Cite has empty unknown parameter:|month=(help); External link in|work= - ^ R. S. MacKay, J. D. Meiss (1987). Hamiltonian Dynamical Systems: A Reprint Selection. CRC Press. p. 36. ISBN 0852742053.
- ^ "Inseparable galactic twins". ESA/Hubble Picture of the Week. Retrieved 12 July 2013.
- ^ The Admiralty (1987). Admiralty manual of navigation. Vol. 1. The Stationery Office. p. 277. ISBN 978-0-11-772880-6., Chapter 11, p. 277
- ^ Newton, Isaac (1729). The mathematical principles of natural philosophy. Vol. 2. p. 307. ISBN 978-0-11-772880-6., Book 3, Proposition 36, Page 307 Newton put the force to depress the sea at places 90 degrees distant from the Sun at "1 to 38604600" (in terms of g), and wrote that the force to raise the sea along the Sun-Earth axis is "twice as great" (i.e., 2 to 38604600) which comes to about 0.52 × 10−7 g as expressed in the text.
وصلات خارجية
- Gravitational Tides by J. Christopher Mihos of Case Western Reserve University
- Audio: Cain/Gay – Astronomy Cast Tidal Forces – July 2007.
- Gray, Meghan; Merrifield, Michael. "Tidal Forces". Sixty Symbols. Brady Haran for the University of Nottingham.
- Pau Amaro Seoane. "Stellar collisions: Tidal disruption of a star by a massive black hole". Retrieved 2018-12-28.
- Myths about Gravity and Tides by Mikolaj Sawicki of John A. Logan College and the University of Colorado.
- Tidal Misconceptions by Donald E. Simanek