سلسلي

هذا المقال هو عن المنحنى الرياضي. إذا كنت تريد الاستخدامات الأخرى، انظر سلسلي (توضيح).

"Chainette" redirects here. For the wine grape also known as Chainette, see Cinsaut.

A chain hanging from points forms a catenary.

Freely-hanging overhead power lines also form a catenary (most prominently visible with high-voltage lines, and with some imperfection near to the insulators).

الحرير في بيت عنكبوت يشكل العديد من السلسليات المرنة.

منحني سلسلي إنگليزية: catenary أو كاتينا في الفيزياء والهندسة الرياضية هو شكل هندسي نظري يتشكل عند تدلي سلسلة أو سلك عندما تكون طرفيها مثبتين في الأعلى وذلك تحت تأثير قوة الثقالة الأرضية (وزن الجسم المعلق).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الوصف الرياضي

Catenaries for different values of a

 المعادلة العامة

تعطى معادلة شكل المنحني الكاتينري بتابع جيب التمام للقطع الزائد بالشكل:

$$y=a\cosh \left({\frac {x}{a}}\right)={\frac {a}{2}}\left(e^{\frac {x}{a}}+e^{-{\frac {x}{a}}}\right)$$

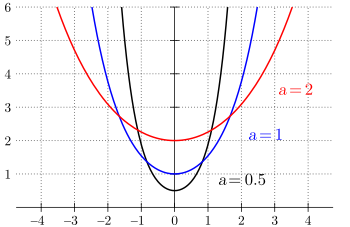
حيث cosh is the hyperbolic cosine function, and where x is measured from the lowest point. All catenary curves are similar to each other, since changing the parameter a is equivalent to a uniform scaling of the curve.

The Whewell equation for the catenary is

$$\tan \varphi ={\frac {s}{a}}\,.$$

Differentiating gives

$${\frac {d\varphi }{ds}}={\frac {\cos ^{2}\varphi }{a}}$$

and eliminating φ gives the Cesàro equation

$$\kappa ={\frac {a}{s^{2}+a^{2}}}\,.$$

The radius of curvature is then

$$\rho =a\sec ^{2}\varphi$$

which is the length of the line normal to the curve between it and the x-axis.

 العلاقة مع المنحنيات الأخرى

When a parabola is rolled along a straight line, the roulette curve traced by its focus is a catenary. The envelope of the directrix of the parabola is also a catenary. The involute from the vertex, that is the roulette traced by a point starting at the vertex when a line is rolled on a catenary, is the tractrix.

Another roulette, formed by rolling a line on a catenary, is another line. This implies that square wheels can roll perfectly smoothly on a road made of a series of bumps in the shape of an inverted catenary curve. The wheels can be any regular polygon except a triangle, but the catenary must have parameters corresponding to the shape and dimensions of the wheels.

 الخصائص الهندسية

Over any horizontal interval, the ratio of the area under the catenary to its length equals a, independent of the interval selected. The catenary is the only plane curve other than a horizontal line with this property. Also, the geometric centroid of the area under a stretch of catenary is the midpoint of the perpendicular segment connecting the centroid of the curve itself and the x-axis.

 العلوم

A moving charge in a uniform electric field travels along a catenary (which tends to a parabola if the charge velocity is much less than the speed of light c).

The surface of revolution with fixed radii at either end that has minimum surface area is a catenary revolved about the x-axis.

 التحليل

 نموذج السلاسل والعقود

In the mathematical model the chain (or cord, cable, rope, string, etc.) is idealized by assuming that it is so thin that it can be regarded as a curve and that it is so flexible any force of tension exerted by the chain is parallel to the chain. The analysis of the curve for an optimal arch is similar except that the forces of tension become forces of compression and everything is inverted. An underlying principle is that the chain may be considered a rigid body once it has attained equilibrium. Equations which define the shape of the curve and the tension of the chain at each point may be derived by a careful inspection of the various forces acting on a segment using the fact that these forces must be in balance if the chain is in static equilibrium.

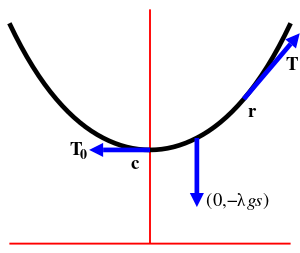
Let the path followed by the chain be given parametrically by r = (x, y) = (x(s), y(s)) where s represents arc length and r is the position vector. This is the natural parameterization and has the property that

$${\frac {d\mathbf {r} }{ds}}=\mathbf {u}$$

where u is a unit tangent vector.

Diagram of forces acting on a segment of a catenary from c to r. The forces are the tension T₀ at c, the tension T at r, and the weight of the chain (0, −λgs). Since the chain is at rest the sum of these forces must be zero.

A differential equation for the curve may be derived as follows. Let c be the lowest point on the chain, called the vertex of the catenary. The slope dy/dx of the curve is zero at c since it is a minimum point. Assume r is to the right of c since the other case is implied by symmetry. The forces acting on the section of the chain from c to r are the tension of the chain at c, the tension of the chain at r, and the weight of the chain. The tension at c is tangent to the curve at c and is therefore horizontal without any vertical component and it pulls the section to the left so it may be written (−T₀, 0) where T₀ is the magnitude of the force. The tension at r is parallel to the curve at r and pulls the section to the right. The tension at r can be split into two components so it may be written Tu = (T cos φ, T sin φ), where T is the magnitude of the force and φ is the angle between the curve at r and the x-axis (see tangential angle). Finally, the weight of the chain is represented by (0, −λgs) where λ is the mass per unit length, g is the gravitational field strength and s is the length of the segment of chain between c and r.

The chain is in equilibrium so the sum of three forces is 0, therefore

$$T\cos \varphi =T_{0}$$

and

$$T\sin \varphi =\lambda gs\,,$$

and dividing these gives

$${\frac {dy}{dx}}=\tan \varphi ={\frac {\lambda gs}{T_{0}}}\,.$$

It is convenient to write

$$a={\frac {T_{0}}{\lambda g}}$$

which is the length of chain whose weight is equal in magnitude to the tension at c. Then

$${\frac {dy}{dx}}={\frac {s}{a}}$$

is an equation defining the curve.

The horizontal component of the tension, T cos φ = T₀ is constant and the vertical component of the tension, T sin φ = λgs is proportional to the length of chain between r and the vertex.

 اشتقاق المعادلات للمنحنى

The differential equation given above can be solved to produce equations for the curve.

من

$${\frac {dy}{dx}}={\frac {s}{a}}\,,$$

the formula for arc length gives

$${\frac {ds}{dx}}={\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}={\frac {\sqrt {a^{2}+s^{2}}}{a}}\,.$$

Then

$${\frac {dx}{ds}}={\frac {1}{\frac {ds}{dx}}}={\frac {a}{\sqrt {a^{2}+s^{2}}}}$$

and

$${\frac {dy}{ds}}={\frac {\frac {dy}{dx}}{\frac {ds}{dx}}}={\frac {s}{\sqrt {a^{2}+s^{2}}}}\,.$$

The second of these equations can be integrated to give

$$y={\sqrt {a^{2}+s^{2}}}+\beta$$

and by shifting the position of the x-axis, β can be taken to be 0. Then

$$y={\sqrt {a^{2}+s^{2}}}\,,\quad y^{2}=a^{2}+s^{2}\,.$$

The x-axis thus chosen is called the directrix of the catenary.

It follows that the magnitude of the tension at a point (x, y) is T = λgy, which is proportional to the distance between the point and the directrix.

This tension may also be expressed as T = T₀ y/a .

The integral of the expression for dx/ds can be found using standard techniques, giving

$$x=a\operatorname {arsinh} \left({\frac {s}{a}}\right)+\alpha \,.$$

and, again, by shifting the position of the y-axis, α can be taken to be 0. Then

$$x=a\operatorname {arsinh} \left({\frac {s}{a}}\right)\,,\quad s=a\sinh \left({\frac {x}{a}}\right)\,.$$

The y-axis thus chosen passes through the vertex and is called the axis of the catenary.

These results can be used to eliminate s giving

$$y=a\cosh \left({\frac {x}{a}}\right)\,.$$

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 اشتقاق بديل

The differential equation can be solved using a different approach. From

$$s=a\tan \varphi$$

it follows that

$${\frac {dx}{d\varphi }}={\frac {dx}{ds}}{\frac {ds}{d\varphi }}=\cos \varphi \cdot a\sec ^{2}\varphi =a\sec \varphi$$

and

$${\frac {dy}{d\varphi }}={\frac {dy}{ds}}{\frac {ds}{d\varphi }}=\sin \varphi \cdot a\sec ^{2}\varphi =a\tan \varphi \sec \varphi \,.$$

Integrating gives,

$$x=a\ln(\sec \varphi +\tan \varphi )+\alpha$$

and

$$y=a\sec \varphi +\beta \,.$$

As before, the x and y-axes can be shifted so α and β can be taken to be 0. Then

$$\sec \varphi +\tan \varphi =e^{\frac {x}{a}}\,,$$

and taking the reciprocal of both sides

$$\sec \varphi -\tan \varphi =e^{-{\frac {x}{a}}}\,.$$

Adding and subtracting the last two equations then gives the solution

$$y=a\sec \varphi =a\cosh \left({\frac {x}{a}}\right)\,,$$

and

$$s=a\tan \varphi =a\sinh \left({\frac {x}{a}}\right)\,.$$

 تحديد المتغيرات

Three catenaries through the same two points, depending on the horizontal force T_H.

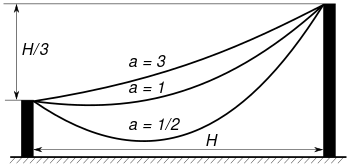
In general the parameter a is the position of the axis. The equation can be determined in this case as follows:

Relabel if necessary so that P₁ is to the left of P₂ and let H be the horizontal and v be the vertical distance from P₁ to P₂. Translate the axes so that the vertex of the catenary lies on the y-axis and its height a is adjusted so the catenary satisfies the standard equation of the curve

$$y=a\cosh \left({\frac {x}{a}}\right)$$

and let the coordinates of P₁ and P₂ be (x₁, y₁) and (x₂, y₂) respectively. The curve passes through these points, so the difference of height is

$$v=a\cosh \left({\frac {x_{2}}{a}}\right)-a\cosh \left({\frac {x_{1}}{a}}\right)\,.$$

and the length of the curve from P₁ to P₂ is

$$s=a\sinh \left({\frac {x_{2}}{a}}\right)-a\sinh \left({\frac {x_{1}}{a}}\right)\,.$$

When s² − v² is expanded using these expressions the result is

$$s^{2}-v^{2}=2a^{2}\left(\cosh \left({\frac {x_{2}-x_{1}}{a}}\right)-1\right)=4a^{2}\sinh ^{2}\left({\frac {H}{2a}}\right)\,,$$

so

$${\sqrt {s^{2}-v^{2}}}=2a\sinh \left({\frac {H}{2a}}\right)\,.$$

This is a transcendental equation in a and must be solved numerically. It can be shown with the methods of calculus that there is at most one solution with a > 0 and so there is at most one position of equilibrium.

However, if both ends of the curve (P₁ and P₂) are at the same level (y₁ = y₂), it can be shown that

$$a={\frac {{\frac {1}{4}}L^{2}-h^{2}}{2h}}\,$$

where L is the total length of the curve between P₁ and P₂ and h is the sag (vertical distance between P₁, P₂ and the vertex of the curve).

It can also be shown that

$$L=2a\sinh {\frac {H}{2a}}\,$$

and

$$H=2a\operatorname {arcosh} {\frac {h+a}{a}}\,$$

where H is the horizontal distance between P₁ and P₂ which are located at the same level (H = x₂ − x₁).

The horizontal traction force at P₁ and P₂ is T_H = aw, where w is the mass per unit length of the chain or cable.

 Variational formulation

Consider a chain of length $L$ suspended from two points of equal height and at distance $D$. The curve has to minimize its potential energy

$$U=\int _{0}^{D}g\rho y{\sqrt {1+y'^{2}}}dx$$

and is subject to the constraint

$$\int _{0}^{D}{\sqrt {1+y'^{2}}}dx=L\,.$$

The modified Lagrangian is therefore

$${\mathcal {L}}=(g\rho y-\lambda ){\sqrt {1+y'^{2}}}$$

where $\lambda$ is the Lagrange multiplier to be determined. As the independent variable $x$ does not appear in the Lagrangian, we can use the Beltrami identity

$${\mathcal {L}}-y'{\frac {\partial {\mathcal {L}}}{\partial y'}}=C$$

where $C$ is an integration constant, in order to obtain a first integral

$${\frac {(g\rho y-\lambda )}{\sqrt {1+y'^{2}}}}=-C$$

This is an ordinary first order differential equation that can be solved by the method of separation of variables. Its solution is the usual hyperbolic cosine where the parameters are obtained from the constraints.

 التعميمات مع قوة رأسية

 سلاسل غير منتظمة

If the density of the chain is variable then the analysis above can be adapted to produce equations for the curve given the density, or given the curve to find the density.

Let w denote the weight per unit length of the chain, then the weight of the chain has magnitude

$$\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,$$

where the limits of integration are c and r. Balancing forces as in the uniform chain produces

$$T\cos \varphi =T_{0}$$

and

$$T\sin \varphi =\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,$$

and therefore

$${\frac {dy}{dx}}=\tan \varphi ={\frac {1}{T_{0}}}\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,.$$

Differentiation then gives

$$w=T_{0}{\frac {d}{ds}}{\frac {dy}{dx}}={\frac {T_{0}{\dfrac {d^{2}y}{dx^{2}}}}{\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}}\,.$$

In terms of φ and the radius of curvature ρ this becomes

$$w={\frac {T_{0}}{\rho \cos ^{2}\varphi }}\,.$$

 Suspension bridge curve

Golden Gate Bridge. Most suspension bridge cables follow a parabolic, not a catenary curve, because the roadway is much heavier than the cable.

A similar analysis can be done to find the curve followed by the cable supporting a suspension bridge with a horizontal roadway. If the weight of the roadway per unit length is w and the weight of the cable and the wire supporting the bridge is negligible in comparison, then the weight on the cable (see the figure in Catenary#Model of chains and arches) from c to r is wx where x is the horizontal distance between c and r. Proceeding as before gives the differential equation

$${\frac {dy}{dx}}=\tan \varphi ={\frac {w}{T_{0}}}x\,.$$

This is solved by simple integration to get

$$y={\frac {w}{2T_{0}}}x^{2}+\beta$$

and so the cable follows a parabola. If the weight of the cable and supporting wires is not negligible then the analysis is more complex.

 سلسلي متساوي القوة

In a catenary of equal strength, the cable is strengthened according to the magnitude of the tension at each point, so its resistance to breaking is constant along its length. Assuming that the strength of the cable is proportional to its density per unit length, the weight, w, per unit length of the chain can be written T/c, where c is constant, and the analysis for nonuniform chains can be applied.

In this case the equations for tension are

$${\begin{aligned}T\cos \varphi &=T_{0}\,,\\T\sin \varphi &={\frac {1}{c}}\int T\,ds\,.\end{aligned}}$$

Combining gives

$$c\tan \varphi =\int \sec \varphi \,ds$$

and by differentiation

$$c=\rho \cos \varphi$$

where ρ is the radius of curvature.

The solution to this is

$$y=c\ln \left(\sec \left({\frac {x}{c}}\right)\right)\,.$$

In this case, the curve has vertical asymptotes and this limits the span to πc. Other relations are

$$x=c\varphi \,,\quad s=\ln \left(\tan \left({\frac {\pi +2\varphi }{4}}\right)\right)\,.$$

The curve was studied 1826 by Davies Gilbert and, apparently independently, by Gaspard-Gustave Coriolis in 1836.

Recently, it was shown that this type of catenary could act as a building block of electromagnetic metasurface and was known as "catenary of equal phase gradient".

 سلسلي مرن

In an elastic catenary, the chain is replaced by a spring which can stretch in response to tension. The spring is assumed to stretch in accordance with Hooke's Law. Specifically, if p is the natural length of a section of spring, then the length of the spring with tension T applied has length

$$s=\left(1+{\frac {T}{E}}\right)p\,,$$

where E is a constant equal to kp, where k is the stiffness of the spring. In the catenary the value of T is variable, but ratio remains valid at a local level, so

$${\frac {ds}{dp}}=1+{\frac {T}{E}}\,.$$

The curve followed by an elastic spring can now be derived following a similar method as for the inelastic spring.

The equations for tension of the spring are

$$T\cos \varphi =T_{0}\,,$$

and

$$T\sin \varphi =\lambda _{0}gp\,,$$

from which

$${\frac {dy}{dx}}=\tan \varphi ={\frac {\lambda _{0}gp}{T_{0}}}\,,\quad T={\sqrt {T_{0}^{2}+\lambda _{0}^{2}g^{2}p^{2}}}\,,$$

where p is the natural length of the segment from c to r and λ₀ is the mass per unit length of the spring with no tension and g is the gravitational field strength. Write

$$a={\frac {T_{0}}{\lambda _{0}g}}$$

so

$${\frac {dy}{dx}}=\tan \varphi ={\frac {p}{a}}\quad {\text{and}}\quad T={\frac {T_{0}}{a}}{\sqrt {a^{2}+p^{2}}}\,.$$

Then

$${\begin{aligned}{\frac {dx}{ds}}&=\cos \varphi ={\frac {T_{0}}{T}}\\[6pt]{\frac {dy}{ds}}&=\sin \varphi ={\frac {\lambda _{0}gp}{T}}\,,\end{aligned}}$$

from which

$${\begin{alignedat}{3}{\frac {dx}{dp}}&={\frac {T_{0}}{T}}{\frac {ds}{dp}}&&=T_{0}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {a}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}}{E}}\\[6pt]{\frac {dy}{dp}}&={\frac {\lambda _{0}gp}{T}}{\frac {ds}{dp}}&&={\frac {T_{0}p}{a}}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {p}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}p}{Ea}}\,.\end{alignedat}}$$

Integrating gives the parametric equations

$${\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p+\alpha \,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}+\beta \,.\end{aligned}}$$

Again, the x and y-axes can be shifted so α and β can be taken to be 0. So

$${\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p\,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}\end{aligned}}$$

are parametric equations for the curve. At the rigid limit where E is large, the shape of the curve reduces to that of a non-elastic chain.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تعميمات أخرى

 Chain under a general force

With no assumptions being made regarding the force G acting on the chain, the following analysis can be made.

First, let T = T(s) be the force of tension as a function of s. The chain is flexible so it can only exert a force parallel to itself. Since tension is defined as the force that the chain exerts on itself, T must be parallel to the chain. In other words,

$$\mathbf {T} =T\mathbf {u} \,,$$

where T is the magnitude of T and u is the unit tangent vector.

Second, let G = G(s) be the external force per unit length acting on a small segment of a chain as a function of s. The forces acting on the segment of the chain between s and s + Δs are the force of tension T(s + Δs) at one end of the segment, the nearly opposite force −T(s) at the other end, and the external force acting on the segment which is approximately GΔs. These forces must balance so

$$\mathbf {T} (s+\Delta s)-\mathbf {T} (s)+\mathbf {G} \Delta s\approx \mathbf {0} \,.$$

Divide by Δs and take the limit as Δs → 0 to obtain

$${\frac {d\mathbf {T} }{ds}}+\mathbf {G} =\mathbf {0} \,.$$

These equations can be used as the starting point in the analysis of a flexible chain acting under any external force. In the case of the standard catenary, G = (0, −λg) where the chain has mass λ per unit length and g is the gravitational field strength.

 هندسة معمارية

قوس تخت كسرى في المدائن كما تبدو اليوم هي تقريباً وليس بالضبط كاتينا.

Arches under the roof of Gaudí's كازا ميلا, Barcelona, Spain that are close to catenaries.

Gaudi's catenary model at Casa Milà

القوس السلسلي هو محل هندسي للنقط التي كل منها تحمل نفس الوزن من مجموع الوزن الكلي للقوس، ولهذا يُستخدم في إنشاء الهياكل المعماريه. الهياكل التي تُصنع بشكل سلسلي تعاني من قوة الشد فقط، كما يحدث في الحبال التي تدعم الجسور معلقه. أو من قوة الضغط عندما الهيكل يبنى على شكل منعكس بالنسبة إلى خط افقي ، كما هو الحال في هياكل القبب (على سبيل المثال قبة في سانت بول في لندن التي صممها روبرت هوك وفي الأقواس التي صممها لاول مرة المهندس الإسباني انطونيو كاودي. بعد ذلك أُستخدم القوس السلسلي في الهندسه المعماريه وفي بناء الجسور (على سبيل المثال في جسور مايلارت وفي السكك الحديديه لكارابيت ).

The Sheffield Winter Garden is enclosed by a series of catenary arches.

 انظر أيضاً

• Catenary arch
• Chain fountain or self-siphoning beads
• Overhead catenary – power lines suspended over rail or tram vehicles
• Roulette (curve) – an elliptic/hyperbolic catenary
• Troposkein – the shape of a spun rope
• Weighted catenary
• جسر معلق

 وصلات خارجية

• O'Connor, John J.; Robertson, Edmund F., "Catenary", MacTutor History of Mathematics archive, University of St Andrews .
• قالب:PlanetMath
• Catenary curve calculator
• Catenary at The Geometry Center
• "Catenary" at Visual Dictionary of Special Plane Curves
• The Catenary - Chains, Arches, and Soap Films.
• Cable Sag Error Calculator – Calculates the deviation from a straight line of a catenary curve and provides derivation of the calculator and references.
• Dynamic as well as static cetenary curve equations derived – The equations governing the shape (static case) as well as dynamics (dynamic case) of a centenary is derived. Solution to the equations discussed.
• The straight line, the catenary, the brachistochrone, the circle, and Fermat Unified approach to some geodesics.
• Ira Freeman "A General Form of the Suspension Bridge Catenary" Bulletin of the AMS