سطح دوراني

A portion of the curve

x = 2 + cos(z)

rotated around the

z

-axis

A torus as a square revolved around an axis along the diagonal of the square.

أسطح دورانية

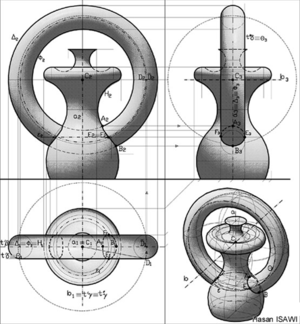
السطح الدوراني Surface of revolution يتولد من دوران خط g (مستقيم او منحني) حول خط مستقيم ثابت a , في هذة الحالة نطلق على الخط المتحرك g راسم السطح وعلى a محور الدوران. يجب الاخذ بعين الاعتبار ان معظم انواع السطوح الدوارنية تنتج في الحالة التي فيها , الخطوط g a ينتموا الى نفس السطح (complanari)

المنحني الذي يحصل علية كنتيجة تقاطع السطح الدوراني بسطح عمودي على محور الدوران، يسمى منحني موازي(Parallel)
المنحني الذي يحصل علية كنتيجة تقاطع السطح الدوراني بسطح يمر بمحور الدوران، يسمى منحنى الطول (meridian)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

الأنواع

حسب طبيعية راسم السطح g (مستقيم أو منحني), تتولد السطوح التالية:

1- في الحالة التي يكون فيها g خط مستقيم (conica degenere), السطح الدوراني الناتج هو:
- - مخروط عندما g يتقاطع مع a في نقطة V حقيقية
- - اسطوانة عندما g يتقاطع مع a في نقطة V∞ خيالية
2- في الحالة التي يكون فيها g منحنى، السطح الناتج هو:

- سطح ثنائي دوراني، عندما تكون g مقطع مخروطي (اهليج، قطع مكافئ، قطع زائد)، وبحيث يكون محور الدوران متطابق مع محور من محاور القطع المخروطي^[1] - سطح دوراني عام، عندما تكون g أي نوع من المنحنيات التي لم يسبق ذكرها.

الخصائص

The sections of the surface of revolution made by planes through the axis are called meridional sections. Any meridional section can be considered to be the generatrix in the plane determined by it and the axis.^[2]

The sections of the surface of revolution made by planes that are perpendicular to the axis are circles.

Some special cases of hyperboloids (of either one or two sheets) and elliptic paraboloids are surfaces of revolution. These may be identified as those quadratic surfaces all of whose cross sections perpendicular to the axis are circular.

Area formula

If the curve is described by the parametric functions $x (t)$ , $y (t)$ , with $t$ ranging over some interval $[a, b]$ , and the axis of revolution is the $y$ -axis, then the area $A y$ is given by the integral

A_{y}=2\pi \int _{a}^{b}x(t)\,{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}\,dt,

provided that $x (t)$ is never negative between the endpoints $a$ and $b$ . This formula is the calculus equivalent of Pappus's centroid theorem.^[3] The quantity

{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}

comes from the Pythagorean theorem and represents a small segment of the arc of the curve, as in the arc length formula. The quantity $2π x (t)$ is the path of (the centroid of) this small segment, as required by Pappus' theorem.

Likewise, when the axis of rotation is the $x$ -axis and provided that $y (t)$ is never negative, the area is given by^[4]

A_{x}=2\pi \int _{a}^{b}y(t)\,{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}\,dt.

If the continuous curve is described by the function $y = f (x)$ , $a \leq x \leq b$ , then the integral becomes

A_{x}=2\pi \int _{a}^{b}y{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}\,dx=2\pi \int _{a}^{b}f(x){\sqrt {1+{\big (}f'(x){\big )}^{2}}}\,dx

for revolution around the $x$ -axis, and

A_{y}=2\pi \int _{a}^{b}x{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}\,dx

for revolution around the y-axis (provided $a \geq 0$ ). These come from the above formula.^[5]

For example, the spherical surface with unit radius is generated by the curve $y (t) = sin(t)$ , $x (t) = cos(t)$ , when $t$ ranges over $[0,π]$ . Its area is therefore

{\begin{aligned}A&{}=2\pi \int _{0}^{\pi }\sin(t){\sqrt {{\big (}\cos(t){\big )}^{2}+{\big (}\sin(t){\big )}^{2}}}\,dt\\&{}=2\pi \int _{0}^{\pi }\sin(t)\,dt\\&{}=4\pi .\end{aligned}}

For the case of the spherical curve with radius $r$ , $y (x) = \sqrt r 2 - x 2$ rotated about the $x$ -axis

{\begin{aligned}A&{}=2\pi \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,{\sqrt {1+{\frac {x^{2}}{r^{2}-x^{2}}}}}\,dx\\&{}=2\pi r\int _{-r}^{r}\,{\sqrt {r^{2}-x^{2}}}\,{\sqrt {\frac {1}{r^{2}-x^{2}}}}\,dx\\&{}=2\pi r\int _{-r}^{r}\,dx\\&{}=4\pi r^{2}\,\end{aligned}}

A minimal surface of revolution is the surface of revolution of the curve between two given points which minimizes surface area.^[6] A basic problem in the calculus of variations is finding the curve between two points that produces this minimal surface of revolution.^[6]

There are only two minimal surfaces of revolution (surfaces of revolution which are also minimal surfaces): the plane and the catenoid.^[7]

تعبيرات إحداثية

A surface of revolution given by rotating a curve described by $y=f(x)$ around the x-axis may be most simply described by $y^{2}+z^{2}=f(x)^{2}$ . This yields the parametrization in terms of $x$ and $\theta$ as $(x,f(x)\cos(\theta ),f(x)\sin(\theta ))$ . If instead we revolve the curve around the y-axis, then the curve is described by $y=f({\sqrt {x^{2}+z^{2}}})$ , yielding the expression $(x\cos(\theta ),f(x),x\sin(\theta ))$ in terms of the parameters $x$ and $\theta$ .

If x and y are defined in terms of a parameter $t$ , then we obtain a parametrization in terms of $t$ and $\theta$ . If $x$ and $y$ are functions of $t$ , then the surface of revolution obtained by revolving the curve around the x-axis is described by $(x(t),y(t)\cos(\theta ),y(t)\sin(\theta ))$ , and the surface of revolution obtained by revolving the curve around the y-axis is described by $(x(t)\cos(\theta ),y(t),x(t)\sin(\theta ))$ .

Geodesics

Meridians are always geodesics on a surface of revolution. Other geodesics are governed by Clairaut's relation.^[8]

الأسطح الحلقية

مقال رئيسي: سطح حلقي

سطح حلقي مولّد من مربع

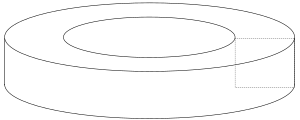
A surface of revolution with a hole in, where the axis of revolution does not intersect the surface, is called a toroid.^[9] For example, when a rectangle is rotated around an axis parallel to one of its edges, then a hollow square-section ring is produced. If the revolved figure is a circle, then the object is called a torus.

التطبيقات

The use of surfaces of revolution is essential in many fields in physics and engineering. When certain objects are designed digitally, revolutions like these can be used to determine surface area without the use of measuring the length and radius of the object being designed.

معرض

يمكن تفسير السطح الزائدي الدائري على أنه سطح مغلف كرة بينما هذه تتحول على طول قطعين زائدين متقابلين

مراجع

^ Geometric Loci Archived 2022-06-19 at the Wayback Machine
^ Wilson, W.A.; Tracey, J.I. (1925), Analytic Geometry (Revised ed.), D.C. Heath and Co., p. 227
^ Thomas, George B. "6.7: Area of a Surface of Revolution; 6.11: The Theorems of Pappus". Calculus (3rd ed.). pp. 206–209, 217–219. LCCN 69016407.
^ Singh, R.R. (1993). Engineering Mathematics (6 ed.). Tata McGraw-Hill. p. 6.90. ISBN 0-07-014615-2.
^ Swokowski, Earl W. (1983), Calculus with analytic geometry (Alternate ed.), Prindle, Weber & Schmidt, p. 617, ISBN 0-87150-341-7, https://archive.org/details/calculuswithanal00swok/page/617
^ ^أ ^ب Eric W. Weisstein, Minimal Surface of Revolution at MathWorld.
^ Eric W. Weisstein, Catenoid at MathWorld.
^ Pressley, Andrew. “Chapter 9 - Geodesics.” Elementary Differential Geometry, 2nd ed., Springer, London, 2012, pp. 227–230.
^ Eric W. Weisstein, Toroid at MathWorld.

انظر أيضاً

سطح كروي
Channel surface, a generalisation of a surface of revolution
Gabriel's Horn
Generalized helicoid
Lemon (geometry), surface of revolution of a circular arc
Liouville surface, another generalization of a surface of revolution
Spheroid
Surface integral
Translation surface (differential geometry)

المراجع

وصلات خارجية

Eric W. Weisstein, Surface of Revolution at MathWorld.
"Surface de révolution". Encyclopédie des Formes Mathématiques Remarquables (in French).{{cite web}}: CS1 maint: unrecognized language (link)

هذه بذرة مقالة عن الهندسة الرياضية تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها.

[1] Geometric Loci Archived 2022-06-19 at the Wayback Machine

[2] Wilson, W.A.; Tracey, J.I. (1925), Analytic Geometry (Revised ed.), D.C. Heath and Co., p. 227

[3] Thomas, George B. "6.7: Area of a Surface of Revolution; 6.11: The Theorems of Pappus". Calculus (3rd ed.). pp. 206–209, 217–219. LCCN 69016407.

[4] Singh, R.R. (1993). Engineering Mathematics (6 ed.). Tata McGraw-Hill. p. 6.90. ISBN 0-07-014615-2.

[5] Swokowski, Earl W. (1983), Calculus with analytic geometry (Alternate ed.), Prindle, Weber & Schmidt, p. 617, ISBN 0-87150-341-7, https://archive.org/details/calculuswithanal00swok/page/617

[Mathworld:_Minimal_Surface_of_Revolution-6] أ ^ب Eric W. Weisstein, Minimal Surface of Revolution at MathWorld.

[7] Eric W. Weisstein, Catenoid at MathWorld.

[8] Pressley, Andrew. “Chapter 9 - Geodesics.” Elementary Differential Geometry, 2nd ed., Springer, London, 2012, pp. 227–230.

[9] Eric W. Weisstein, Toroid at MathWorld.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]