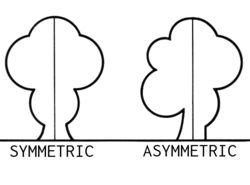
تناظر

التناظر Symmetry خاصية يمكن وصف العديد من الأشياء بها مثل الأجسام الهندسية و المعادلات الرياضية وغيرها ، و بشكل عام نقول عن جسم ما أنه متناظر بالنسبة لعملية ما ، إذا كان تطبيق هذه العملية عليه لا تحدث فيه تغيرا . يمكن إطلاق وصف التناظر على أي غرض object أو بنية structure فنقول انها متناظرة بالنسبة للعملية Process كذا .. . الغرض أو البنية يمكن أن تكون بلورة ، بلاطة أرضية ، جزيئة ، أو حتى غرض مجرد abstract object مثل معادلة رياضية أو مجموعة من النغمات الموسيقية tones . طبيعة التغيير أو الإجراء المطبق يمكن ان تكون متنوعة من عمليات بسيطة بديهية كان ترحك شكلا هندسيا أو دائرة حول قطرها او يمكن ان تكون تحويلا للمعادلات او في طريقة العزف الموسيقي .
يمكن لبعض التناظرات ان تكون مألوفة جدا لدرجة لا يمكن لنا تمميزها بدون تنبيه . فالمرآة مثلا مثال شهير لأحد أدوات خلق التناظر تقوم بقلب جانبي للأشياء بحيث يصبح الطرف الأيمن أيسرا و الأسير أيمنا . عملية التمييز تصبح أسهل عندما يكون الجانبين الأيمن و الأيسر من مخلوق ما مختلفين جذريا . لكن التناظر عند الأحياء و خاصة عند الإنسان متطور جدا بحيث يصعب ملاحظة مثل هذه الفوارق .
ستتناول المقالة عدة انواع من التناظر أهمها : التناظر الرياضي (في الرياضيات) و فيها يكون التناظر معرف و محدد بشكل دقيق ، الثاني تطبيق التناظر على العلوم و التكنولوجيا . مثلا التناظر و تطبيقاته في النتائج الأساسية للفيزياء الحديثة ، بما في ذلك مناحي الزمكان . النوع الثالث هو تاريخ الاستخدام الواسع للتناظر في التاريخ و العمارة و الفنون و حتى الأديان .
زمرة التقايسات في الفضاء الإقليدي
إن المجموعة المكونة من جميع التقايسات في الفضاء، أي من جميع التقايسات المباشرة ومن جميع التناظرات بالنسبة للنقط والتناظرات بالنسبة للمستويات تشكل زمرة[ر] غير تبادلية بالنسبة لعملية تركيب التحويلات. وإن مجموعة جميع التقايسات المباشرة تشكل زمرة جزئية من زمرة التقايسات. إن كل تقايس في الفضاء هو إما أن يكون التحويل المطابق أو تناظراً بالنسبة لمستو أو جداء تناظرين بالنسبة لمستويين أو جداء ثلاثة تناظرات بالنسبة لثلاثة مستويات أو جداء أربعة تناظرات بالنسبة لأربعة مستويات.
ويبرهن أن كل تقايس مباشر في المستوي هو جداء تناظرين بالنسبة لمستقيمين واقعين في هذا المستوي، فهو بالتالي إما انسحاب وإما دوران، ويبرهن أن كل تقايس غير مباشر في المستوي هو تناظر انزلاقي أو انعكاسي انزلاقي glide reflection. والتناظر الانزلاقي هو جداء تناظر بالنسبة لمستقيم في انسحاب يوازي متجهه محور التناظر.
إن مجموعة جميع الانسحابات تشكل زمرة تبادلية بالنسبة لعملية تركيب التحويلات، ذلك لأن تركيب كل انسحابين هو انسحاب، والتحويل المطابق م هو العنصر المحايد، والتحويل المحاكي لانسحاب هو انسحاب، وعملية تركيب الانسحابات تخضع للخاصتين التجمعية والتبادلية. إن زمرة الانسحابات هي زمرة جزئية من زمرة التقايسات.
أما مجموعة جميع التقايسات غير المباشرة فلا تشكل زمرة بالنسبة لعملية تركيب التحويلات لأن تركيب كل تقايسين غير مباشرين هو تقايس مباشر.
ومن الأسئلة التي ترد في نطاق زمرة التقايسات، هو السؤال عن التقايسات في المستوي التي تنقل كل مربع ب حـ د هـ، إلى نفسه. من الواضح أنه لا يوجد أي انسحاب أو أي تناظر انزلاقي يحول المربع إلى نفسه. فالتقايسات الممكنة هي دورانات وتناظرات. وفي الواقع إن التحويلات التالية تنقل المربع إلى نفسه: التحويل المطابق، الدورانات حول مركز المربع بزوايا قدرها +90ْ، +180ْ، +270ْ، التناظران بالنسبة لقطري المربع، التناظران بالنسبة لمستقيمين اللذين يمر كل منهما بمنتصفي ضلعين متقابلين من المربع. إن هذه التقايسات الثمانية تشكل زمرة منتهية بالنسبة لعملية تركيب التطبيقات. وهذا يعني أن تركيب أي من عناصر هذه الزمرة يعطي كذلك تحويلاً ينقل المربع إلى نفسه. إن هذه الزمرة تشتمل على جميع العناصر المطلوبة.
تناظرات المكعب
يقال عن جسم إنه ذو محور دوران axis of rotation من المرتبة ن إذا لم يتغير شكله العام نتيجة دورانه حول هذا المحور بزاوية قدرها . فالمضلع المنتظم الذي عدد أضلاعه ن لا يتغير شكله العام إذا ما دوِّر حول محور عمودي على مستويه عند مركزه بزاوية تساوي أحد مضاعفات الزاوية . ومن الواضح أن أي محور دوران من المرتبة 2 (محور دوران ثنائي) هو محور تناظر للشكل.
ويلاحظ أن للمكعب الخواص التناظرية الآتية:
أ ـ المكعب متناظر بالنسبة لمركزه (والذي هو نقطة تقاطع أقطاره)
ب ـ للمكعب ثلاثة محاور دوران رباعية (من المرتبة الرابعة)، يمر كل منها بمركزيْ وجهين متقابلين منه. إن هذه المحاور الثلاثة متعامدة مثنى.
حـ ـ للمكعب أربعة محاور دوران ثلاثية (من المرتبة الثالثة) هي أقطاره. وهذا يعني أن المكعب لا يتغير شكله العام نتيجة دوران زاويته حول كلٍ من هذه الأقطار.
د ـ للمكعب ستة محاور دوران ثنائية، يُحصل عليها بوصل منتصفي كل ضلعين متقابلين.
هـ ـ للمكعب ثلاثة مستويات تناظرية عمودية على محاور الدوران الرباعية وتمر بمركز المكعب.
و ـ للمكعب ستة مستويات تناظرية عمودية على محاور الدوران الثنائية وتتعين بالأزواج الستة للأضلاع المتقابلة.
إن عناصر التناظر هذه هي أيضاً عناصر تناظرية لثماني الوجوه المنتظم الذي يحصل عليه بوصل كل مركز من مراكز وجوه المكعب مع مراكز الوجوه المجاورة له.
التناظر في عالم الأحياء
تلاحظ تناظرات محورية في الأجزاء الأكثر انتظاماً من النباتات (كالأزهار) أو في بعض الحيوانات المائية المثبتة (كعديدات الأرجل Polyps). والتناظرات المحورية هذه هي من مرتبة غير منتهية أو من مرتبة منتهية. ففي النباتات أحاديات الفلقة monocotyledones تكون هذه المرتبة 3 أو 6، وفي معظم النباتات ثنائيات الفلقة[ر] dicotyledones وفي شائكات الجلدة échinodermes وفي معائيات الجوف[ر] Coelentérés 4 أو 6 أو 8. وقد يظهر تناظر ثنائي الجانب نتيجة للتراكب تحت تأثير التطور (كما في الأزهار زيجية الشكل zyomorphes وفي قنافد البحر[ر] oursins غير المنتظمة). ولا يلاحظ لدى الحيوانات السريعة الحركة كالفقاريات [ر] Verteprés ومفصليات الأرجل[ر] Arthopes سوى تناظرات ثنائية الجانب.
ولدى عدد من ذوات المصراعين[ر] يقال لها متساوية الجوانب ومتباينة المصاريع (كصدفة القديس جاك والمحار) ولدى الأسماك المنبسطة pleutonectes (سمك موسى وسمك الترس) يلاحظ أن المستوي البدائي للتناظر قد استبدل به مستو عمودي عليه.
وقلما يلاحظ تناظر من النمط الكروي الدوراني حول مركز ما في الهيكل العظمي للكائنات وحيدات الخلية (كالشعاعيات).
وأما تناظر المشطيات فوحيد من نوعه فهو حول مستويين متعامدين محورهما المشترك أمامي خلفي.
ومما لا شك فيه أنه كلما ازداد التعقيد في الكائن الحي قليلاً كان لبعض أجهزته تناظر مختلف عن ذاك التناظر للكائن بكامله. فالتناظر التقريبي لفك الإنسان مثلاً عمودي على تناظر الجسم وأما تناظر المقلة فمحوري إلخ..
وأخيراً فإن التناظر الخارجي قد يخفي في بعض الأحيان عدم تناظر داخلي، ففي الإنسان تكون المعدة على اليسار أما الكبد والزائدة الدودية فعلى اليمين.
التماثل في السفن والخزف والمعدن
تماثل في لحاف
تماثل في سجاد
التماثل في الحرف والفنون
تناظر أخلاقي
أنظر ايضا
- Symmetry group
- Chirality
- Fixed points of isometry groups in Euclidean space - center of symmetry
- Spontaneous symmetry breaking
- Gödel, Escher, Bach
- M. C. Escher
- Wallpaper group
- Asymmetry
- Asymmetric rhythm
- Even and odd functions
- Symmetries of polyominoes
- Symmetries of polyiamonds
- Burnside's lemma
- Symmetry (biology)
- Spacetime symmetries
- Time symmetry
- Semimetric, which is sometimes translated as symmetric in Russian texts.
- Symmetric relation
المصادر
- Darvas, György (2007). Symmetry, Basel-Berlin-Boston: Birkhäuser Verlag, xi + 508 p.
- Hahn, Werner (1998). Symmetry As A Developmental Principle In Nature And Art World Scientific. ISBN 981-02-2363-3.
- Livio, Mario (2005). The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry. New York: Simon & Schuster. ISBN 0-7432-5820-7.
- Perle, George (1990). The Listening Composer, p. 112. California: University of California Press. ISBN 0-520-06991-9.
- Perle, George (1992). Symmetry, the Twelve-Tone Scale, and Tonality. Contemporary Music Review 6 (2), pp. 81-96.
- Petitjean, Michel (2003). Chirality and Symmetry Measures: A Transdisciplinary Review. Entropy 5(3), pp. 271-312.
- Petitjean, Michel (2007). A Definition of Symmetry, Symmetry: Culture and Science 18(2-3), pp. 99-119.
- Rosen, Joe, 1995. Symmetry in Science: An Introduction to the General Theory. Springer-Verlag.
- Symmetry: Culture and Science, published by Symmetrion, Budapest. ISSN 0865-4824.
- Weyl, Hermann (1982). Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3.
{{cite book}}: Cite has empty unknown parameter:|coauthors=(help); Unknown parameter|origdate=ignored (|orig-date=suggested) (help)
وصلات خارجية
| Symmetry
]].- An Analysis of the first movement of the Fourth String Quartet (1928) by Andrew Kuster
- Skaalid: Design Theory
- Mathforum: Symmetry/Tesselations
- Calotta: A World of Symmetry
- Dutch: Symmetry Around a Point in the Plane
- Saw: Design Notes
- Chapman: Aesthetics of Symmetry
- Abas: The Wonder Of Symmetry
- ISIS Symmetry
- Symmetry and Asymmetry at The Dictionary of the History of Ideas
- Examples of asymmetry in musical waveforms
- International Symmetry Association - ISA
- Institute Symmetrion
- Professor Ian Stewart on the history of symmetry
- Photographs of Symmetrical Cloisters
- Symmetry and Symmetry Measures: General Definitions