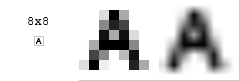تحويل جيب التمام المتقطع

DCT-II (في الأسفل) مقارنة بـ DFT (في الوسط) لإشارة إدخال (في الأعلى).

يعبر تحويل جيب التمام المتقطع discrete cosine transformation (DCT) عن تسلسل محدود من نقاط البيانات من حيث مجموع وظائف جيب التمام المتذبذبة عند ترددات مختلفة. DCT ، التي اقترحها أولاً ناصر أحمد عام 1972 ، هي تقنية تحويل مستخدمة على نطاق واسع في معالجة الإشارة و ضغط البيانات. يتم استخدامها في معظم الوسائط الرقمية ، بما في ذلك الصور الرقمية (مثل JPEG و HEIF ، حيث يمكن التخلص من المكونات الصغيرة عالية التردد) ، الڤيديو الرقمي (مثل MPEG و H.26x) ، الصوت الرقمي (مثل Dolby Digital ، MP3 و AAC ) ، تلفزيون رقمي (مثل SDTV ، HDTV و VOD) ، راديو رقمي (مثل AAC + و DAB +) و ترميز الكلام (مثل AAC-LD و Siren و Opus). تعتبر DCTs مهمة أيضًا للعديد من التطبيقات الأخرى في العلوم والهندسة ، مثل معالجة الإشارات الرقمية و أجهزة الاتصالات وتقليل استخدام عرض النطاق الترددي للشبكة و الطرق الطيفية للحل العددي لـ المعادلات التفاضلية الجزئية.

تحويل جيب التمام المتقطع discrete cosine transformation تحويل رياضي له عدة إستخدامات في التقنيات الرقمية و خاصة في ميدان معالجة الإشارة الرقمية. من أشهر تطبيقات هذا التحويل خوارزميات ضغط JEPEG و MPEG و MP3.

يعد استخدام جيب التمام بدلاً من توابع الجيب أمرًا بالغ الأهمية للضغط ، حيث اتضح (كما هو موضح أدناه) أن هناك حاجة إلى عدد أقل من وظائف التمام لتقريب إشارة نموذجية ، في حين المعادلات التفاضلية تجيب جيب التمام عن اختيار معين لـ شروط الحدود. على وجه الخصوص ، فإن DCT هي التحويل المتعلق بـ فورييه تشبه تحويل فورييه المتقطع (DFT) ، ولكن باستخدام الرقم الحقيقي فقط. ترتبط DCTs عمومًا بمعاملات سلسلة فورييه لتسلسل ممتد دوريًا ومتماثلًا ، في حين ترتبط DFTs بمعامل سلسلة فورييه لسلسلة ممتدة دوريًا. DCTs تعادل DFTs تقريبًا ضعف الطول ، وتعمل على بيانات حقيقية مع تناظر الزوجية (بما أن تحويل فورييه لتابع حقيقي وزوجي هو حقيقي وزوجي) ، بينما في بعض المتغيرات المدخلات و / أو بيانات الإخراج يتم إزالتها بمقدار نصف عينة. هناك ثمانية متغيرات قياسية من DCT ، أربعة منها شائعة.

النوع الأكثر شيوعًا لتحويل جيب التمام المتقطع هو النوع الثاني من DCT ، والذي غالبًا ما يطلق عليه ببساطة "DCT". كان هذا هو DCT الأصلي كما اقترحه أحمد لأول مرة. غالبًا ما يطلق على عكسها ، النوع الثالث من DCT ، ببساطة "عكس DCT" أو "IDCT". هناك تحويلان مرتبطان هما تحويل الجيب المتقطع (DST) ، وهو ما يعادل DFT للوظائف الحقيقية و "الفردية" ، و تحويل جيب التمام المتقطع المعدل (MDCT) ، والذي يعتمد على DCT للبيانات "المتداخلة". تم تطوير DCTs متعددة الأبعاد (MD DCTs) لتوسيع مفهوم DCT على إشارات MD. هناك العديد من الخوارزميات لحساب MD DCT. تم تطوير مجموعة متنوعة من الخوارزميات السريعة لتقليل التعقيد الحسابي لتنفيذ DCT. أحد هذه هو العدد الصحيح DCT[1] (IntDCT) ، عدد صحيح تقريب لـ DCT القياسي,[2] مستخدم في العديد من المعايير الدولية ISO / IEC و ITU-T.[2][1]

ضغط DCT ، المعروف أيضًا باسم ضغط الكتلة ، يضغط البيانات في مجموعات من كتل DCT متقطعة.[3] يمكن أن تحتوي كتل DCT على عدد من الأحجام ، بما في ذلك 8x8 پكسل لـ DCT القياسية ، وأحجام DCT الصحيحة المتنوعة بين 4 × 4 و 32 × 32 پكسل.[1][4] DCT لديه خاصية قوية "لضغط الطاقة",[5][6] وقادرة على تحقيق جودة عالية في نسب ضغط عالية للبيانات.[7][8] ومع ذلك ، يمكن أن تظهر الصنعيات الانضغاطية ممتلئة عند تطبيق ضغط DCT ثقيل.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تاريخ

ناصر أحمد, مخترع تحويل جيب التمام المتقطع (DCT) ، الذي اقترحه لأول مرة في عام 1972.

تم تصميم تحويل جيب التمام المتقطع (DCT) لأول مرة بواسطة ناصر أحمد ، أثناء العمل في جامعة ولاية كانساس ، واقترح المفهوم على مؤسسة العلوم الوطنية في عام 1972. كان يقصد في الأصل DCT لـ ضغط الصور.[9][1] طور أحمد خوارزمية DCT عملية مع طالب الدكتوراه تي. ناتارجان وصديقه ك. ر. راو في جامعة تكساس في أرلنگتون في عام 1973 ، ووجدوا أنها كانت الخوارزمية الأكثر فعالية لضغط الصورة.[9] وقد قدموا نتائجهم في ورقة يناير 1974 ، بعنوان "تحويل جيب التمام المتقطع".[5][6][10]وصفت ما يسمى الآن من النوع الثاني DCT (DCT-II),[11] وكذلك DCT معكوس من النوع الثالث (IDCT).[5] كان المنشور القياسي,[12][13] وقد تم الاستشهاد به كتطور أساسي في آلاف الأعمال منذ نشره.[14] تم تلخيص الأعمال والأحداث البحثية الأساسية التي أدت إلى تطوير DCT في منشور لاحق من قبل أحمد ، "كيف أكون مع تحويل جيب التمام المتقطع".[9]

منذ تقديمه في عام 1974 ، كان هناك بحث كبير على DCT.[10] في عام 1977 ، نشر ون سيونگ تشن ورقة مع سي هاريسون سميث وستانلي سي فراليك تقدم خوارزمية DCT سريعة ،[15][10] وأسس مختبرات ضغط لتسويق تقنية DCT.[1] وتشمل التطورات الأخرى ورقة 1978 من م.جي. ناراسيما و أ.م. پيترسن ، وورقة عام 1984 بقلم بي جي. لي.[10] أشادت مجموعة خبراء التصوير الفوتوغرافي بهذه الأوراق البحثية ، إلى جانب ورقة أحمد الأصلية لعام 1974 وورقة تشن 1977 ، كأساس لخوارزمية ضغط الصور ذات فقد JPEG في عام 1992.[10][16]

في عام 1975 ، قام جون أ. رويس و گونر س. روبنسن بتكييف DCT لـ تعويض الحركة بين الإطارات ترميز الفيديو. لقد جربوا DCT و تحويل فورييه السريع (FFT) ، حيث قاموا بتطوير أجهزة ترميز هجينة بين الإطارات لكليهما ، ووجدوا أن DCT هي الأكثر كفاءة نظرًا لتعقيدها المنخفض ، وقادرة على ضغط بيانات الصورة حتى 0.25 - بت لكل پكسل لمشهد فيديو تليفوني بجودة صورة مماثلة لمبرمج داخل الإطار يتطلب 2 بت لكل پكسل.[17][18] تم تطبيق DCT على ترميز الفيديو بواسطة ون-سيونگ تشن,[1] الذي طور خوارزمية DCT سريعة مع سي.ه. سمث و س.سي فرالك في 1977,[19][10]وأُسست Compression Labs لتسويق تقنية DCT.[1] في عام 1979 ، قام آنيل ك. جين و جسوات ر. جين أيضًا بتطوير ضغط الفيديو DCT المعوض عن الحركة,[20][21] يسمى أيضًا تعويض حركة الكتلة.[21] أدى ذلك إلى قيام تشن بتطوير خوارزمية ضغط فيديو عملية ، تسمى DCT المعوضة بالحركة أو تشفير المشهد التكيفي ، في عام 1981.[21]أصبح DCT المعوض عن الحركة لاحقًا تقنية الترميز القياسية لضغط الفيديو من أواخر الثمانينيات فصاعدًا.[22][23]

يتم استخدام DCT الصحيح في ترميز الفيديو المتقدم (AVC),[24][1] تم تقديمه عام 2003 ، و ترميز فيديو عالي الكفاءة (HEVC),[4][1] تم تقديمه في عام 2013. يستخدم DCT الصحيح أيضًا في تنسيق الصورة عالي الكفاءة (HEIF) ، والذي يستخدم مجموعة فرعية من تنسيق ترميز الفيديو HEVC لتشفير الصور الثابتة.[4]

تم تطوير DCT متغير ، تحويل جيب التمام المتقطع المعدل (MDCT) ، من قبل جون پي. پرنسن ، أ.و. جونسون وألان برادلي في جامعة ساري عام 1987,[25] بعد العمل السابق ال1ي قام به پرنسن و برادلي عام 1986[26] يتم استخدام MDCT في معظم تنسيقات الضغط الصوتي ، مثل Dolby رقمي (AC-3),[27][28] MP3 (التي تستخدم DCT الهجينة - خوارزمية FFT),[29] ترميز صوتي متقدم (AAC),[30] و Vorbis (Ogg).[31]

تم اشتقاق تحويل الجيب المتقطع (DST) من DCT ، عن طريق استبدال شرط نيومان عند x = 0 بـ شرط ديرخليه.[32]تم وصف DST في ورقة DCT 1974 بواسطة أحمد وناتراجان وراو.[5] تم وصف نوع DST من النوع الأول (DST-I) لاحقًا بواسطة أنيل ك. جين في عام 1976 ، ثم نوع DST من النوع الثاني (DST-II) وصفها HB Kekra and جي.ك. سولانكا عام 1978.[33]

طور ناصر أحمد أيضًا خوارزمية DCT بدون فقد مع گريدار مانديم و نيراج ماگوترا في جامعة نيو مكسيكو في عام 1995. ويسمح هذا باستخدام تقنية DCT لـ ضغط بدون فقد للصور. إنه تعديل لخوارزمية DCT الأصلية ، ويتضمن عناصر DCT معكوسة و تعديل دلتا. إنها خوارزمية انضغاط أكثر فاعلية من ترميز الأنتروبي.[34] تُعرف DCT بدون فقدان أيضًا باسم LDCT.[35]

بدأ ترميز Wavelet باستخدام تحويلات المويجات في ضغط الصور بعد تطوير تشفير DCT.[36] أدى إدخال DCT إلى تطوير تشفير المويجات ، وهو نوع مختلف من تشفير DCT يستخدم الموجات بدلاً من الخوارزمية المستندة إلى كتلة DCT.[36] تحويل المويجات المنفصلة (DWT) يستخدم التشفير في معيار JPEG 2000,[37] تم تطويره من 1997 إلى 2000.[38] يعد ترميز Wavelet أكثر كثافة في المعالج ، ولم يشهد بعد انتشارًا واسعًا في الاستخدام الذي يواجه المستهلك.[39]


تطبيقات

DCT هي تقنية التحويل الأكثر استخدامًا في معالجة الإشارة,[40] وإلى حد بعيد التحول الخطي الأكثر استخدامًا في ضغط البيانات.[41] كان ضغط البيانات DCT أمرًا أساسيًا في الثورة الرقمية.[8][42][43] كانت الوسائط الرقمية غير المضغوطة بالإضافة إلى الضغط دون فقد بشكل غير عملي و ذاكرة و عرض النطاق الترددي كبيرين، والتي تم تقليلها بشكل كبير من خلال DCT ذات الكفاءة العالية بتقنية الضغط ذو الفقد,[7][8] قادر على تحقيق نسبة ضغط البيانات من 8: 1 إلى 14: 1 لجودة قريبة من الاستوديو,[7] حتى 100: 1 للمحتوى ذي الجودة المقبولة.[8]أدى الاعتماد الواسع لمعايير ضغط DCT إلى ظهور وانتشار تقنيات الوسائط الرقمية ، مثل الصور الرقمية ، الرسومات الرقمية,[44][45] الفيديو الرقمي,[22][43] البث الإعلامي,[46]تلفزيون رقمي بث مباشر فيديو عند الطلب (VOD),[8] السينما الرقمية,[27] فيديو عالي الدقة (HD video), و التلفزيون عالي الدقة (HDTV).[7][47]

غالبًا ما يتم استخدام DCT ، وعلى وجه الخصوص DCT-II ، في معالجة الإشارات والصور ، خاصة للضغط ذو الفقد ، لأنه يتميز بخاصية "ضغط طاقة" قوية:[5][6] في التطبيقات النموذجية ، تميل معظم معلومات الإشارة إلى التركيز في عدد قليل من مكونات التردد المنخفض من DCT. بالنسبة إلى عملية ماركوڤ المرتبطة ارتباطًا وثيقًا ، يمكن لـ DCT الاقتراب من كفاءة الضغط لـ تحويل كارونن-لوڤ (وهو الأمثل من حيث علاقة الديكور). كما هو موضح أدناه ، ينبع هذا من شروط الحدود الضمنية في وظائف جيب التمام.

تستخدم DCTs أيضًا على نطاق واسع في حل المعادلات التفاضلية الجزئية عن طريق الأساليب الطيفية ، حيث تتوافق المتغيرات المختلفة لـ DCT مع شروط الحدود الزوجية / الفردية المختلفة قليلاً عند طرفي المصفوفة.

ترتبط DCTs أيضًا ارتباطًا وثيقًا بـ كثيرات الحدود تشيبيشيڤ ، ويتم استخدام خوارزميات DCT السريعة (أدناه) في تقريب تشيبيشيڤ من الوظائف العشوائية من خلال سلسلة من كثيرات الحدود تشيبيشيڤ، على سبيل المثال في تربيع كلنشو-كرتس.

DCT هو معيار الترميز لـ أجهزة الاتصالات الوسائط المتعددة. ويستخدم على نطاق واسع لتقليل معدل البت وتقليل الاستخدام عرض النطاق الترددي للشبكة.[1] يقلل ضغط DCT من مقدار الذاكرة وعرض النطاق المطلوب لـ الإشارات الرقمية بشكل ملحوظ.[8]

تطبيقات عامة

يستخدم DCT على نطاق واسع في العديد من التطبيقات ، والتي تشمل ما يلي.

معايير الوسائط المرئية DCT

للمزيد من المعلومات: JPEG#Discrete cosine transform

يعتبر DCT-II ، المعروف أيضًا باسم DCT ، هو الأسلوب الأكثر أهمية لضغط الصورة.[بحاجة لمصدر] يتم استخدامه في معايير ضغط الصور مثل JPEG و ضغط الفيديو والمعايير مثل H.26x و MJPEG و MPEG و DV و Theora و Daala. هناك ، DCT-II ثنائي الأبعاد من يتم حساب الكتل والنتائج هي الكمّي و الترميز الأنتروپي. في هذه الحالة, عادة ما تكون 8 ويتم تطبيق صيغة DCT-II على كل صف وعمود من الكتلة. والنتيجة هي مصفوفة معامل تحويل 8 × 8 فيها العنصر (أعلى اليسار) هو مكون DC (التردد الصفري) والإدخالات مع زيادة قيم المؤشر الرأسي والأفقي تمثل ترددات مكانية رأسية وأفقية أعلى.

ترميز الفيديو المتقدم (AVC) يستخدم العدد الصحيح لـ DCT[24][1] (IntDCT), تقريب صحيح لـ DCT.[2][1] ويستخدم كتل DCT 4 × 4 و 8 × 8 عدد صحيح. ترميز فيديو عالي الكفاءة (HEVC) و تنسيق صور عالي الكفاءة (HEIC) يستخدمان أحجام فدرة DCT صحيحة متعددة تتراوح بين 4 × 4 و 32 × 32 پكسل.[4][1] اعتبارا من 2019, يعد AVC إلى حد بعيد التنسيق الأكثر استخدامًا لتسجيل وضغط وتوزيع محتوى الفيديو ، ويستخدمه 91٪ من مطوري الفيديو ، يليه HEVC الذي يستخدمه 43٪ من المطورين.[55]

تشكيلات الصورة

معيار ضغط الصورة العام تطبيقات شائعة
JPEG[1] 1992 المعيار الأكثر استخدامًا ضغط الصور[64][65] وتنسيق الصورة الرقمية,[58]
JPEG XR 2009 Open XML Paper Specification
WebP 2010 تنسيق رسومي يدعم الضغط ذو الفقد من الصور الرقمية. طُور بواسطة گوگل.
تنسيق صورة عالي الكفاءة (HEIF) 2013 تنسيق ملف صورة بناءً على ضغط HEVC. يحسن الضغط على JPEG,[66] ويدعم التحريك مع ضغط أكثر كفاءة بكثير من تنسيق animated GIF.[67]
BPG 2014 يعتمد على ضغط HEVC

تشكيلات الفيديو

معيار ترميز الفيديو العام تطبيقات شائعة
H.261[68][69] 1988 الأولى من عائلة معايير ترميز الفيديو. تُستخدم بشكل أساسي في المنتجات القديمة مؤتمرات الفيديو و هاتف الفيديو.
Motion JPEG (MJPEG)[70] 1992 QuickTime, تحرير الفيديو, التحرير اللاخطي, الكاميرات الرقمية
MPEG-1 Video[71] 1993 الفيديو الرقمي التوزيع على CD أو عبر شبكة الانترنت.
MPEG-2 Video (H.262)[71] 1995 تخزين ومعالجة الصور الرقمية في تطبيقات البث ، التلفزيون الرقمي ، HDTV ، الكبل ، الأقمار الصناعية ، توزيع الفيديو عالي السرعة إنترنت ، DVD
DV 1995 كاميرا فيديو, الكاسيت الرقمي
H.263 (MPEG-4 Part 2)[68] 1996 الهاتفية المرئية عبر شبكة الهاتف بتبديل عام (PSTN) H.320 الشبكة الرقمية للخدمات المتكاملة (ISDN)[72][73]
الترميز الفيديوي المتقدم (AVC / H.264 / MPEG-4)[1][24] 2003 الأكثر شيوعًا فيديو عالي الدقة تنسيق التسجيل / الضغط / التوزيع ، البث فيديو الإنترنت ، YouTube عمليات بث، Blu-ray Discs ، HDTV ، متصفحات الويب ، البث التلفزيوني ، الأجهزة المحمولة ، الأجهزة الاستهلاكية ، Netflix,[54] الهاتفية الرقمية, Facetime[53]
Theora 2004 فيديو الانترنت, مستعرض الشبكة
VC-1 2006 وسائط وندوز, Blu-ray Discs
Apple ProRes 2007 الإنتاج الفيديوي الاحترافي.[62]
WebM فيديو 2010 تنسيق وسائط متعددة مفتوح المصدر تم تطويره بواسطة گوگل مخصص للاستخدام مع HTML5.
ترميز فيديو عالي الكفاءة (HEVC / H.265)[1][4] 2013 الخليفة الصاعد لمعيار H.264 / MPEG-4 AVC ، مع قدرة ضغط محسنة بشكل كبير.
Daala 2013


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

MDCT معايير الصوت

للمزيد من المعلومات: Modified discrete cosine transform

الصوت بشكل عام

معيار ضغط الصوت عام تطبيقات شائعة
Dolby Digital (AC-3)[27][28] 1991 سينما, السينما الرقمية, DVD, Blu-ray, بث وسائل الإعلام, ألعاب الفيديو
الترميز الصوتي للتحويل التكيفي (ATRAC)[27] 1992 MiniDisc
MPEG Layer III (MP3)[29][1] 1993 توزيع الصوت الرقمي, MP3 مشغلات, مشغلات الوسائط المحمولة, بث وسائل الإعلام
مشفر الصوت الإدراكي (PAC)[27] 1996 خدمة الراديو السمعي الرقمي (DARS)
التشفير الصوتي المتقدم (AAC / MP4 Audio)[30][27] 1997 توزيع الصوت الرقمي , مشغلات الوسائط المحمولة, بث وسائل الإعلام, game consoles, أجهزة المحمول, iOS, آي تيونز, أندرويد, بلاك بيري
ترميز صوتي عالي الكفاءة (AAC+)[74][75] 1997 الراديو الرقمي, البث الصوتي الرقمي (DAB+),[50] الراديو العلمي الرقمي (DRM)
Cook Codec 1998 RealAudio
وسائط صوت وندوز (WMA)[27] 1999 وسائط وندوز
Vorbis[31][27] 2000 توزيع الصوت الرقمي ، محطات الراديو ، وسائط البث ، ألعاب الفيديو ، Spotify ، ويكيپيديا
ترميز عالي الوضوح (HDC)[51] 2002 راديو رقمي, HD Radio
التكيف مع الدقة الديناميكية (DRA)[27] 2008 معيار الصوت الوطني الصيني, بث الوسائط المتعددة المتنقلة في الصين, DVB-H
Dolby AC-4[76] 2017 ATSC 3.0, تلفزيون شديد الوضوح (UHD TV)
MPEG-H 3D Audio[77]

تشفير الكلام

معيار تشفير الكلام عام تطبيقات شائعة
AAC-LD (LD-MDCT)[78] 1999 Mobile telephony, voice-over-IP (VoIP), iOS, FaceTime[53]
Siren[52] 1999 VoIP, wideband audio, G.722.1
G.722.1[79] 1999 VoIP, wideband audio, G.722
G.729.1[80] 2006 G.729, VoIP, wideband audio,[80] mobile telephony
EVRC-WB[81] 2007 Wideband audio
G.718[82] 2008 VoIP, wideband audio, mobile telephony
G.719[81] 2008 Teleconferencing, videoconferencing, voice mail
CELT[83] 2011 VoIP,[84][85] mobile telephony
Opus[86] 2012 VoIP,[87] mobile telephony, WhatsApp,[88][89][90] PlayStation 4[91]
Enhanced Voice Services (EVS)[92] 2014 Mobile telephony, VoIP, wideband audio

MD DCT

انظر أيضاً: ZPEG

DCTs متعددة الأبعاد (MD DCTs) لها العديد من التطبيقات ، بشكل رئيسي DCTs ثلاثية الأبعاد مثل 3-D DCT-II ، والتي لديها العديد من التطبيقات الجديدة مثل أنظمة تشفير التصوير الطيفي,[93] ترميز متغير الطول الزمني 3D DCT,[94] ترميز الفيديو كخوارزميات,[95] ترميز الفيديو التكيفي [96] و ضغط 3-D.[97] بسبب التحسين في الأجهزة والبرمجيات وإدخال العديد من الخوارزميات السريعة ، تزداد ضرورة استخدام D-DCTs بسرعة. اكتسب DCT-IV شعبية لتطبيقاته في التنفيذ السريع للمجمعات متعددة المراحل ذات القيمة الحقيقية,[98] تحويل متعامد ملفوف[99][100]وقواعد المويجات المعدلة جيب التمام.[101]

معالجة الإشارات الرقمية

تلعب DCT دورًا مهمًا جدًا في معالجة الإشارات الرقمية. باستخدام DCT ، يمكن ضغط الإشارات. يمكن استخدام DCT في تخطيط كهربية القلب لضغط إشارات تخطيط القلب. يوفر DCT2 نسبة ضغط أفضل من DCT.

يتم تنفيذ DCT على نطاق واسع في معالجات الإشارات الرقمية (DSP) ، بالإضافة إلى برامج معالجة الإشارات الرقمية. قامت العديد من الشركات بتطوير DSPs على أساس تقنية DCT. يتم استخدام DCTs على نطاق واسع لتطبيقات مثل التشفير وفك التشفير والفيديو والصوت و تعدد الإرسال وإشارات التحكم و التشوير و التحويل التناظري إلى الرقمي. تُستخدم DCTs أيضًا بشكل شائع في رقائق تلفزيون عالي الوضوح مشفر / جهاز فك تشفير (HDTV) .[1]

أدوات الضغط

للمزيد من المعلومات: Compression artifact

مشكلة شائعة في ضغط DCT في الوسائط الرقمية هي حظر أدوات ضغط,[102] بسبب كتل DCT.[3] يمكن أن تسبب خوارزمية DCT المستندة إلى الكتلة عند تطبيق أدوات الضغط الثقيل. نظرًا لاستخدام DCT في معظم الصور الرقمية و معايير ترميز الفيديو (مثل تنسيقات JPEG و H.26x و MPEG) ، تنتشر اأدوات لانضغاط الكتلة المستندة إلى DCT على نطاق واسع في الوسائط الرقمية. في خوارزمية DCT ، يتم تقسيم صورة (أو إطار في تسلسل صور) إلى كتل مربعة تتم معالجتها بشكل مستقل عن بعضها البعض ، ثم يتم أخذ DCT من هذه الكتل ، ومعاملات DCT الناتجة مكماة. يمكن أن تتسبب هذه العملية عوائق القطع ، بشكل أساسي عند ارتفاع نسبة ضغط البيانات.[102] يمكن أن يسبب هذا أيضًا تأثير "mosquito noise" ، الموجود بشكل شائع في الفيديو الرقمي (مثل تنسيقات MPEG).[103]

غالبًا ما تُستخدم كتل DCT في صنع خلل.[3] استفادت الفنانة روزا منكمان من الأدوات التي تعتمد على DCT في صنع خللها,[104] ولا سيما كتل DCT الموجودة في معظم تنسيقات الوسائط الرقمية مثل JPEG الصور الرقمية و MP3 الصوت الرقمي.[3] مثال آخر هو "Jpegs" من قبل المصور الألماني توماس راف ، والذي يستخدم القطع الأثرية المتعمدة JPEG كأساس لنمط الصورة.[105][106]

نظرة عامة غير اصطلاحية

مثل أي تحويل متعلق بفورييه ، فإن تحويلات جيب التمام المتقطعة (DCTs) تعبر عن دالة أو إشارة من حيث مجموع الجيوب مع ترددات مختلفة و سعات مختلفة. مثل تحويل فورييه المتقطع (DFT) ، يعمل DCT على دالة عند عدد محدود من نقاط البيانات المتقطعة. الفرق الواضح بين DCT و DFT هو أن الأول يستخدم وظائف جيب التمام فقط ، بينما يستخدم الأخير كلا من جيب التمام والجيب (في شكل أسي مركب). ومع ذلك ، فإن هذا الاختلاف المرئي هو مجرد نتيجة لتمييز أعمق: تنطوي DCT على حالة الحدود مختلفة من DFT أو غيرها من التحولات ذات الصلة.

يمكن اعتبار التحولات ذات الصلة بـ فورريه التي تعمل على وظيفة عبر مجالات محدودة ، مثل DFT أو DCT أو سلسلة فورريه ، على أنها تحدد ضمنيًا امتداد لتلك الوظيفة خارج المجال. أي بمجرد كتابة دالة كمجموع الجيوب ، يمكنك تقييم هذا المجموع على كل , حتى بالنسبة إلى حيث الأصل لم يتم تحديده. يشير DFT ، مثل سلسلة فورريه، إلى تمديد دورية للتابع الأصلي. إن DCT ، مثل تحويل جيب التمام ، تعني ضمناً تمديد زوجي للتابع الأصلي.

شكل توضيحي للإضافات الزوجية / الفردية الضمنية لبيانات إدخال DCT لـ N = 11 نقطة بيانات (نقاط حمراء) ، للأنواع الأربعة الأكثر شيوعًا من DCT (الأنواع I-IV).

ومع ذلك ، نظرًا لأن DCTs تعمل على تسلسلات "محدودة" و "متقطعة" ، تنشأ مسألتان لا تنطبقان على تحويل جيب التمام المستمر. أولاً ، يتعين على المرء تحديد ما إذا كانت الوظيفة زوجية أو فردية عند حد كل من الحدود اليسرى واليمنى للمجال (أي الحد الأدنى - n والحد الأقصى - n في التعريفات أدناه على التوالي). ثانيًا ، يجب على المرء أن يحدد حول "أي نقطة" تكون الوظيفة زوجية أو فردية. على وجه الخصوص ، ضع في اعتبارك تسلسل "abcd" لأربع نقاط بيانات متساوية المسافات ، ونقول إننا نحدد حدًا "يساريًا" متساويًا. هناك احتمالان معقولان: إما أن تكون البيانات حتى حول العينة "a" ، وفي هذه الحالة يكون الامتداد الزوجي "dcbabcd" ، أو أن البيانات تكون حول النقطة "في منتصف الطريق" بين "" a والنقطة السابقة ، وفي هذه الحالة يكون الامتداد الزوجي dcbaabcd ( a مكرر). تؤدي هذه الاختيارات إلى جميع الاختلافات المعيارية في DCTs وأيضًا تحويل الجيب المنفصل (DSTs). 

يمكن أن يكون كل حد إما زوجيًا أو فرديًا (خياران لكل حد) ويمكن أن يكون متماثلًا حول نقطة بيانات أو النقطة في منتصف المسافة بين نقطتي بيانات (خياران لكل حد) ، ليصبح المجموع 2 × 2 × 2 × 2 = 16 الاحتمالات. نصف هذه الاحتمالات ، تلك التي يكون فيها الحدود "اليسرى" متساوية ، تتوافق مع 8 أنواع من DCT ؛ النصف الآخر هم 8 أنواع DST.

تؤثر شروط الحدود المختلفة هذه بشدة على تطبيقات التحويل وتؤدي إلى خصائص مفيدة بشكل فريد لمختلف أنواع DCT. بشكل مباشر ، عند استخدام تحويلات ذات صلة فورييه لحل المعادلة التفاضلية الجزئية بواسطة الطريقة الطيفية ، يتم تحديد شروط الحدود مباشرة كجزء من المشكلة التي يتم حلها. أو ، بالنسبة إلى MDCT (بناءً على النوع الرابع من DCT) ، فإن شروط الحدود متورطة بشكل وثيق في الخاصية الحرجة لـ MDCT لإلغاء اسم النطاق المستعار. بطريقة أكثر دقة ، تكون شروط الحدود مسؤولة عن خصائص "ضغط الطاقة" التي تجعل DCTs مفيدة لصورة وضغط الصوت ، لأن الحدود تؤثر على معدل التقارب لأي سلسلة شبيهة بفورييه.

على وجه الخصوص ، من المعروف جيدًا أن أي الانقطاعات في دالة يقلل من معدل التقارب لسلسلة فورييه ، لذلك هناك حاجة إلى المزيد من الجيوب الأنفية لتمثيل الوظيفة بدقة معينة. يحكم نفس المبدأ فائدة DFT والتحويلات الأخرى لضغط الإشارة ؛ كلما كانت الوظيفة أكثر سلاسة ، كلما كانت المصطلحات الأقل في DFT أو DCT مطلوبة لتمثيلها بدقة ، وكلما زاد ضغطها. (هنا ، نعتقد أن DFT أو DCT تقريبية لـ سلسلة فوريير أو سلسلة جيب التمام للدالة ، على التوالي ، من أجل التحدث عن "نعومتها".) ومع ذلك ، فإن الدورية الضمنية يعني DFT أن الانقطاعات تحدث عادة عند الحدود: من غير المرجح أن يكون لأي مقطع عشوائي من الإشارة نفس القيمة عند كل من الحدود اليمنى واليسرى. (تنشأ مشكلة مماثلة لـ DST ، حيث يشير شرط الحد الأيسر الفردي إلى انقطاع لأي تابع لا يحدث أن تكون صفرًا عند هذا الحد.) في المقابل ، DCT حيث يكون حد "كلا" حتى دائمًا ينتج امتدادًا مستمرًا عند الحدود (على الرغم من أن المنحدر غير متوقف عمومًا). هذا هو السبب في أن DCTs ، وخاصة DCTs من الأنواع I و II و V و VI (الأنواع التي لها حدان متساويان) تؤدي بشكل عام بشكل أفضل لضغط الإشارة من DFTs و DSTs. عملياً ، يفضل DCT من النوع الثاني عادةً لمثل هذه التطبيقات ، ويرجع ذلك جزئيًا لأسباب الملاءمة الحسابية.


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تعريف اصطلاحي

من الناحية الرسمية ، فإن تحويل جيب التمام المتقطع هو خطي ، دالة قابلة للانعكاس (حيث يشير إلى مجموعة الأرقام الحقيقية) ، أو ما يعادل "N" × "N" مقلوب مصفوفة. هناك عدة أنواع من DCT مع تعريفات معدلة قليلاً. الأعداد الحقيقية "N" x0, ..., xN-1 تم تحويلهم ل N أرقام حقيقية X0, ..., XN-1 وفقًا لإحدى الصيغ:

DCT-I

يضاعف بعض المؤلفين كذلك x0 و xN-1 بشروط √2, وضرب في المقابل X0 و XN-1 بشروط 1/√2. هذا يجعل مصفوفة DCT-I متعامدة ، إذا ما تضاعف أحدهما بعامل مقياس عام , لكنه يخرق التوافقات المباشرة DFT بالقيمة الحقيقية.

إن DCT-I مكافئ تمامًا (حتى عامل مقياس إجمالي 2) ، إلى DFT من أرقام حقيقية حتى مع التماثل. على سبيل المثال ، DCT-I من N=5 الأرقام الحقيقية "abcde" تعادل تمامًا DFT من ثمانية أرقام حقيقية abcdedcb [ك‍] (حتى التماثل) مقسومًا على اثنين. (على النقيض من ذلك ، تشتمل أنواع DCT من الثاني إلى الرابع على تحول نصف العينة في DFT المكافئ.)

لاحظ ، مع ذلك ، أن DCT-I لم يتم تعريفه لـ N أقل من 2. (يتم تعريف جميع أنواع DCT الأخرى لأي "N" موجبة.)

وبالتالي ، فإن DCT-I يتوافق مع شروط الحدود: xn زوجي حول n = 0 وزوجي حول n = N - 1 ؛ وبالمثل ل Xk.

DCT-II

من المحتمل أن يكون DCT-II هو الشكل الأكثر استخدامًا ، وغالبًا ما يشار إليه ببساطة باسم "the DCT".[5][6]

هذا التحويل مكافئ تمامًا (حتى عامل مقياس إجمالي 2) إلى DFT من المدخلات الحقيقية للتماثل حتى حيث تكون العناصر المفهرسة صفر. أي أنها نصف DFT من مدخلات , حيث e , ل , , و for . يمكن أيضًا تحويل DCT II باستخدام إشارة 2N متبوعة بالضرب بنصف نوبة. ويتضح ذلك من مخول.

يضاعف بعض المؤلفين كذلك X0 بشروط 1/√2 وضرب المصفوفة الناتجة بعامل مقياس عام (انظر أدناه للتغيير المقابل في DCT-III). هذا يجعل مصفوفة DCT-II متعامدة ، ولكن يكسر المراسلات المباشرة مع DFT متساوي حقيقي لمدخلات نصفية. هذا هو التطبيع المستخدم بواسطة ماتلاب ، على سبيل المثال. [107] في العديد من التطبيقات ، مثل JPEG ، يكون القياس تعسفيًا لأنه يمكن دمج عوامل المقياس مع خطوة حسابية لاحقة (على سبيل المثال ، خطوة التكمية في JPEG[108]), ويمكن اختيار مقياس يسمح بحساب DCT مع مضاعفات أقل.[109][110]

يشير DCT-II إلى شروط الحدود: xn زوجي حول n = −1/2 زوجي حول n = N−1/2; Xk زوجي حول k = 0 وفردي حول k = N .

DCT-III

نظرًا لأنه معكوس DCT-II (حتى عامل المقياس ، انظر أدناه) ، يُشار أحيانًا إلى هذا النموذج ببساطة باسم "DCT المعكوس" ("IDCT").[6]

بعض المؤلفين يقسمون x0 بشروط √2 بدلاً من 2 (مما ينتج عنه إجمالي x0/√2 مصطلح) وضرب المصفوفة الناتجة في عامل مقياس عام من (انظر أعلاه للتعرف على التغيير المقابل في DCT-II) ، بحيث يكون DCT-II و DCT-III عبارة عن تبديل لبعضهما البعض. هذا يجعل مصفوفة DCT-III متعامدة ، ولكن يوقف التوافقات المباشرة مع DFT متساوي حقيقي لإخراج نصف المحول.

يشير DCT-III إلى شروط الحدود: xn زوجي حول n = 0 وفردي n = N; Xk زوجي حول k = −1/2 زوجي حول k = N−1/2.

DCT-IV

تصبح مصفوفة DCT-IV متعامدة (وبالتالي ، كونها متناظرة بشكل واضح ، معكوسها الخاص) إذا تم ضربها مرة أخرى بعامل مقياس عام .

يُطلق على متغير من DCT-IV ، حيث يتم تداخل البيانات من التحويلات المختلفة ، تحويل جيب التمام المتقطع المعدل (MDCT).[111]

يشير DCT-IV إلى شروط الحدود: xn زوجي حوالي n = −1/2 و فردي حوالي n = N−1/2; بالمثل ل Xk.

DCT V-VIII

DCTs من الأنواع I-IV تعامل كلا الحدين بشكل ثابت فيما يتعلق بنقطة التماثل: فهي زوجية / فردية حول نقطة بيانات لكل من الحدود أو في منتصف الطريق بين نقطتي بيانات لكلا الحدود. على النقيض من ذلك ، فإن DCTs من الأنواع V-VIII تتضمن حدودًا زوجية / فردية حول نقطة بيانات لحد واحد وفي منتصف الطريق بين نقطتي بيانات للحد الآخر.

بمعنى آخر, أنواع DCT I-IV تعادل DFTs الحقيقية من الترتيب الزوجي (بغض النظر عما إذا كانت N زوجية أو فردية) ، لأن DFT المقابل لها طول2(N−1) (ل DCT-I) أو 4N (for DCT-II/III) أو 8N (for DCT-IV). الأنواع الأربعة الإضافية لتحويل جيب التمام المتقطع[112] تتوافق بشكل أساسي مع DFTs الحقيقية ذات الترتيب الفردي المنطقي ، والتي لها عوامل N ± ½ في مقامات براهين جيب التمام.

ومع ذلك ، يبدو أن هذه المتغيرات نادرا ما تستخدم في الممارسة. أحد الأسباب ، ربما ، هو أن خوارزميات FFT لل DFTs ذات الطول الفردي تكون أكثر تعقيدًا بشكل عام من خوارزميات FFT لل DFTs ذات الطول الزوجي (مثل أبسط خوارزميات radix-2 للأطوال الزوجية فقط) ، وهذا التعقيد المتزايد ينتقل إلى DCTs كما هو موضح أدناه.

(المصفوفة الحقيقية العادية ، DFT بطول واحد (طول فردي) لرقم واحد a ، تقابل DCT-V من الطول N = 1.)

التحويلات العكسية

باستخدام اصطلاحات التطبيع أعلاه ، فإن معكوس DCT-I يتم ضرب DCT-I في 2/(N-1). معكوس DCT-IV مضروبًا في DCT-IV 2/N. معكوس DCT-II مضروبًا في DCT-III 2/N والعكس صحيح.[6]

كما هو الحال مع DFT ، فإن عامل التطبيع أمام تعريفات التحويل هذه هو مجرد تقليد ويختلف بين المعالجات. على سبيل المثال ، يضاعف بعض المؤلفين التحولات في بحيث لا يتطلب معكوس أي عامل مضاعف إضافي. إلى جانب عوامل مناسبة √2 (انظر أعلاه) ، يمكن استخدام هذا لجعل مصفوفة التحويل متعامدة.

DCTs متعددة الأبعاد

المتغيرات متعددة الأبعاد لأنواع DCT المختلفة تتبع مباشرة من التعريفات أحادية البعد: فهي ببساطة منتج منفصل (مكافئ ، تكوين) من DCTs على طول كل بُعد.

M-D DCT-II

على سبيل المثال ، فإن DCT-II ثنائي الأبعاد للصورة أو المصفوفة هي ببساطة DCT-II أحادية البعد ، من الأعلى ، يتم إجراؤها على طول الصفوف ثم على طول الأعمدة (أو العكس). أي أن 2D DCT-II تعطى من الصيغة (حذف التطبيع وعوامل المقياس الأخرى ، كما هو موضح أعلاه):

معكوس DCT متعدد الأبعاد هو مجرد منتج قابل للفصل من معكوس (انعكاسات) DCT (s) أحادية البعد (انظر أعلاه) ، على سبيل المثال يتم تطبيق الانعكاسات أحادية البعد على طول بُعد واحد في كل مرة في خوارزمية عمود الصف.

إن "DCT-II ثلاثي الأبعاد" هو امتداد لـ "DCT-II ثنائي الأبعاد" فقط في فراغ ثلاثي الأبعاد ويمكن حسابه رياضياتياً بواسطة الصيغة

معكوس "3-D DCT-II" "" هو "ثلاثي الأبعاد DCT-III" ويمكن حسابه من الصيغة المقدمة من

من الناحية الفنية ، يُعرف حساب DCT ثنائي الأبعاد أو ثلاثي (أو متعدد) بواسطة تسلسل DCTs أحادية البعد على طول كل بُعد باسم خوارزمية عمود الصف. كما هو الحال مع خوارزميات FFT متعددة الأبعاد ، ومع ذلك ، توجد طرق أخرى لحساب نفس الشيء أثناء إجراء الحسابات بترتيب مختلف (أي تشذير / دمج الخوارزميات للأبعاد المختلفة). بسبب النمو السريع في التطبيقات القائمة على DCT 3-D ، تم تطوير العديد من الخوارزميات السريعة لحساب 3 D DCT-II. يتم تطبيق خوارزميات Vector-Radix لحساب M-D DCT لتقليل التعقيد الحسابي وزيادة السرعة الحسابية. لحساب 3 D DCT-II بكفاءة ، تم تطوير خوارزمية سريعة ، خوارزمية Vector-Radix Decimation in Frequency (VR DIF).

3-D DCT-II VR DIF

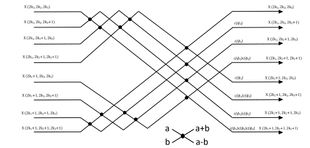
من أجل تطبيق خوارزمية VR DIF ، يجب صياغة بيانات الإدخال وإعادة ترتيبها على النحو التالي.[113][114] حجم التحويل "N x N x N" يفترض أن يكون "2".

المراحل الأساسية الأربع لحساب 3 D DCT-II باستخدام خوارزمية VR DIF.
حيث

يوضح الشكل المجاور المراحل الأربع التي يتم حسابها في 3 D DCT-II باستخدام خوارزمية VR DIF. المرحلة الأولى هي إعادة الترتيب ثلاثي الأبعاد باستخدام تعيين الفهرس الذي توضحه المعادلات أعلاه. المرحلة الثانية هي حساب الفراشة. تحسب كل فراشة ثماني نقاط معًا كما هو موضح في الشكل أدناه ، حيث .

يمكن الآن كتابة النسخة الأصلية ثلاثية الأبعاد DCT-II كـ

حيث .

إذا كانت الأجزاء الزوجية والفردية و ويمكن اعتبار الصيغة العامة لحساب DCT-II ثلاثي الأبعاد على النحو التالي

مرحلة الفراشة الفردية لخوارزمية VR DIF.

حيث

العقديات الحسابية

يحتاج حساب DCT ثلاثي الأبعاد بالكامل مراحل ، وتتضمن كل مرحلة فراشة. يتطلب DCT 3-D كامل أن تحسب الفراشات. تتطلب كل فراشة سبعة مضاعفات حقيقية (بما في ذلك المضاعفات العادية) و 24 إضافات حقيقية (بما في ذلك الإضافات العادية). لذلك ، فإن العدد الإجمالي للمضاعفات الحقيقية اللازمة لهذه المرحلة هو , وإجمالي عدد الإضافات الحقيقية ، أي بما في ذلك الإضافات اللاحقة (الإضافات التكرارية) التي يمكن حسابها مباشرة بعد مرحلة الفراشة أو بعد مرحلة عكس البت من خلال[114] .

تستخدم الطريقة التقليدية لحساب MD-DCT-II نهج صف إطار العمود (RCF) الذي يكون معقدًا من الناحية الحسابية وأقل إنتاجية على معظم أنظمة الأجهزة الحديثة الأكثر تقدمًا. عدد المضاعفات المطلوبة لحساب خوارزمية VR DIF عند مقارنتها بخوارزمية RCF هي عدد قليل جدًا. يتم إعطاء عدد المضاعفات والإضافات التي ينطوي عليها نهج RCF من قبل و respectively. من الجدول 1 ، يمكن ملاحظة أن العدد الإجمالي

TABLE 1 مقارنة خوارزميات VR DIF و RCF لحساب 3D-DCT-II
Transform Size 3D VR Mults RCF Mults 3D VR Adds RCF Adds
8 x 8 x 8 2.625 4.5 10.875 10.875
16 x 16 x 16 3.5 6 15.188 15.188
32 x 32 x 32 4.375 7.5 19.594 19.594
64 x 64 x 64 5.25 9 24.047 24.047

من المضاعفات المرتبطة بخوارزمية DCT VR ثلاثية الأبعاد أقل من تلك المرتبطة بنهج RCF بأكثر من 40٪. بالإضافة إلى ذلك ، يتضمن نهج RCF تبديل المصفوفة والمزيد من الفهرسة وتبديل البيانات من خوارزمية VR الجديدة. وهذا يجعل خوارزمية 3-D DCT VR أكثر كفاءة وأكثر ملاءمة للتطبيقات ثلاثية الأبعاد التي تتضمن 3-D DCT-II مثل ضغط الفيديو وتطبيقات معالجة الصور ثلاثية الأبعاد الأخرى. الاعتبار الرئيسي في اختيار خوارزمية سريعة هو تجنب التعقيدات الحسابية والهيكلية. مع تقدم تقنية أجهزة الكمبيوتر و DSPs ، أصبح وقت تنفيذ العمليات الحسابية (المضاعفات والإضافات) سريعًا جدًا ، ويصبح الهيكل الحسابي المنتظم هو العامل الأكثر أهمية.[115] لذلك ، على الرغم من أن خوارزمية VR ثلاثية الأبعاد المقترحة أعلاه لا تحقق الحد الأدنى النظري لعدد المضاعفات,[116] لديها بنية حسابية أبسط مقارنة بخوارزميات DCT ثلاثية الأبعاد الأخرى. يمكن تنفيذها في مكانها باستخدام فراشة واحدة وتمتلك خصائص Cooley-Tukey FFT algorithm في 3-D. ومن ثم ، يقدم VR ثلاثي الأبعاد خيارًا جيدًا لتقليل العمليات الحسابية في حساب DCT-II ثلاثي الأبعاد مع الحفاظ على البنية البسيطة التي تميز نمط الفراشة خوارزمية Cooley-Tukey FFTs.[[File:DCT-8x8.png|thumb|250px|ترددات DCT ثنائية الأبعاد من JPEG DCT تُظهر الصورة الموجودة على اليمين مجموعة من الترددات الأفقية والعمودية لـ 8 x 8 ()ثنائية الأيعاد DCT. كل خطوة من اليسار إلى اليمين ومن أعلى إلى أسفل هي زيادة في التردد بمقدار 1/2 دورة. على سبيل المثال ، يؤدي تحريك اليمين إلى اليسار من المربع العلوي الأيسر إلى زيادة نصف دورة في التردد الأفقي. حركة أخرى إلى اليمين تنتج نصف دورتين. ينتج عن الحركة الهابطة دورتين نصف أفقياً ونصف دورة رأسياً. يتم تحويل البيانات المصدر (8x8) إلى تركيبة خطية من مربعات التردد 64.

MD-DCT-IV

تعد M-D DCT-IV مجرد امتداد لـ 1-D DCT-IV إلى مجال الأبعاد M. يتم إعطاء DCT-IV ثنائي الأبعاد لمصفوفة أو صورة بواسطة

.

يمكننا حساب MD DCT-IV باستخدام طريقة عمود الصف العادية أو يمكننا استخدام طريقة التحويل متعدد الحدود[117] للحساب السريع والفعال. الفكرة الرئيسية لهذه الخوارزمية هي استخدام تحويل متعدد الحدود لتحويل DCT متعدد الأبعاد إلى سلسلة من DCTs 1-D مباشرة. لدى MD DCT-IV أيضًا العديد من التطبيقات في مختلف المجالات.

حسابات

على الرغم من أن التطبيق المباشر لهذه الصيغ يتطلب O(N2) العمليات ، فمن الممكن لحساب نفس الشيء فقط O(N log N) التعقيد عن طريق حساب الحساب بشكل مشابه لـ تحويل فورييه السريع (FFT). يمكن للمرء أيضا حساب DCTs عبر FFTs مشتركاً مع O(N) خطوات ما قبل وما بعد المعالجة. بشكل عام, O(N log N) تُعرف طرق حساب DCTs باسم خوارزميات تحويل جيب التمام السريع (FCT).

عادة ما تكون الخوارزميات الأكثر كفاءة ، من حيث المبدأ ، هي تلك المتخصصة مباشرة لـ DCT ، على عكس استخدام عمليات إضافية عادية FFT plus O ("N") (انظر أدناه للحصول على استثناء). ومع ذلك ، حتى خوارزميات DCT "المتخصصة" (بما في ذلك جميع تلك التي تحقق أقل عدد حسابي معروف ، على الأقل بالنسبة إلى قوة من حجمين) عادةً ما ترتبط ارتباطًا وثيقًا بخوارزميات FFT - نظرًا لأن DCTs هي بشكل أساسي DFTs من البيانات الحقيقية ، يمكن للمرء تصميم خوارزمية DCT سريعة من خلال أخذ FFT وإلغاء العمليات الزائدة بسبب هذا التناظر. يمكن القيام بذلك تلقائيًا (Frigo & Johnson، 2005). الخوارزميات المستندة إلى Cooley-Tukey FFT algorithm هي الأكثر شيوعًا ، ولكن أي خوارزمية FFT أخرى قابلة للتطبيق أيضًا. على سبيل المثال ، تؤدي خوارزمية Winograd FFT إلى الحد الأدنى من خوارزميات الضرب لـ DFT ، وإن كان ذلك بشكل عام على حساب المزيد من الإضافات ، واقترح Feig & Winograd (1992) خوارزمية مماثلة لـ DCT. نظرًا لأن خوارزميات DFTs و DCTs والتحويلات المماثلة كلها مرتبطة ارتباطًا وثيقًا ، فإن أي تحسن في خوارزميات تحويل واحد سيؤدي نظريًا إلى مكاسب فورية للتحويلات الأخرى أيضًا (Duhamel & Vetterli 1990).

في حين أن خوارزميات DCT التي تستخدم FFT غير المعدلة غالبًا ما يكون لها بعض النفقات النظرية مقارنة بأفضل خوارزميات DCT المتخصصة ، فإن الأولى لها أيضًا ميزة واضحة: برامج FFT المحسنة للغاية متاحة على نطاق واسع. وبالتالي ، من الناحية العملية ، غالبًا ما يكون من الأسهل الحصول على أداء عالي للأطوال العامة "N" باستخدام الخوارزميات القائمة على FFT. (لا يهيمن الأداء على الأجهزة الحديثة عادةً من خلال العمليات الحسابية ، ويتطلب التحسين جهدًا هندسيًا كبيرًا.) من ناحية أخرى ، انظر استخدام واسع النطاق للتحويلات ذات الأحجام الصغيرة والثابتة مثل تستخدم DCT-II في ضغط JPEG ، أو DCTs الصغيرة (أو MDCTs) المستخدمة عادةً في ضغط الصوت. (قد يكون حجم الرمز المنخفض أيضًا سببًا لاستخدام DCT متخصص لتطبيقات الأجهزة المضمنة.)

في الواقع ، حتى خوارزميات DCT التي تستخدم FFT عادية تكافئ أحيانًا تهذيب العمليات الزائدة من FFT أكبر من البيانات المتماثلة الحقيقية ، ويمكن حتى أن تكون مثالية من منظور التهم الحسابية. على سبيل المثال ، DCT من النوع الثاني تعادل DFT من الحجم مع تناظر حقيقي وعناصره المفهرسة هي صفر. تم وصف إحدى الطرق الأكثر شيوعًا لحساب هذا عبر FFT (على سبيل المثال ، الطريقة المستخدمة في FFTPACK و FFTW) بواسطة Narasimha & Peterson (1978) و Makhoul (1980), ويمكن النظر إلى هذه الطريقة بعد فوات الأوان على أنها خطوة واحدة من خوارزمية Cooley-Tukey في الوقت المناسب المطبق على DFT "المنطقي" الحقيقي المتوافق مع DCT II. (تقلل الخطوة الأساسية 4 الحجم DFT إلى أربعة أحجام- DFTs من البيانات الحقيقية ، اثنان منها صفر واثنان منهما يساويان بعضهما البعض بالتناظر الزوجي ، وبالتالي إعطاء حجم واحد- FFT من البيانات الحقيقية بالإضافة إلى الفراشات.) نظرًا لأن العناصر ذات الفهرسة الزوجية تساوي صفرًا ، فإن خطوة radix-4 هذه هي تمامًا مثل خطوة التقسيم الجذري ؛ إذا كان الحجم اللاحق- يتم تنفيذ FFT للبيانات الحقيقية أيضًا بواسطة بيانات حقيقية خوارزمية تقسيم الجذر (كما في Sorensen et al. 1987), ثم تتطابق الخوارزمية الناتجة مع ما كان لفترة طويلة أقل عدد حسابي تم نشره لقوة اثنين DCT-II ( العمليات الحسابية الحقيقية[أ]). يستخدم انخفاض حديث في عدد العمليات أيضاً FFT.[118] لذا ، لا يوجد خطأً جوهريًا في حساب DCT عبر FFT من منظور حسابي - إنه في بعض الأحيان مجرد مسألة ما إذا كانت خوارزمية FFT المقابلة هي الأمثل. (كمسألة عملية ، قد تكون النفقات العامة لاستدعاء الوظائف في استدعاء روتين FFT منفصل مهمة بالنسبة للصغار , ولكن هذا تنفيذ وليس سؤال خوارزمي لأنه يمكن حله عن طريق النشر / التضمين.)

أمثلة على IDCT

مثال يوضح ثمانية مرشحات مختلفة مطبقة على صورة اختبار (أعلى اليسار) بضرب طيف DCT (أعلى اليمين) مع كل مرشح.

ضع في اعتبارك هذه الصورة الرمادية مقاس 8x8 للحرف الكبير A.

الحجم الأصلي ، مقاس 10x (أقرب مجاور) ، مقاس 10x (خطين).
توابع الأساس لتحويل جيب التمام المتقطع مع المعاملات المقابلة (خاصة لصورتنا).
DCT للصورة = .

يتم ضرب كل تابع أساسي في معاملها ثم يضاف هذا المنتج إلى الصورة النهائية.

على اليسار هي الصورة النهائية. في المنتصف توجد دالة الترجيح (مضروبة في معامل) والتي تتم إضافتها إلى الصورة النهائية. على اليمين هي التابع الحالي والمعامل المقابل. يتم تحجيم الصور (باستخدام الاستكمال الثنائي) بواسطة العامل 10 ×.

انظر أيضاً

ملاحظات توضيحية

  1. ^ يعتمد الحساب الدقيق للعمليات الحسابية الحقيقية ، ولا سيما عدد المضاعفات الحقيقية ، إلى حد ما على قياس تعريف التحويل. العد هو لتعريف DCT-II الموضح هنا ؛ يمكن حفظ مضاعفين إذا تم قياس التحويل بشكل عام... عامل . يمكن حفظ مضاعفات إضافية إذا سمح المرء بإعادة مخرجات التحويل بشكل فردي ، كما هو موضح من قبلArai, Agui & Nakajima (1988) حالة الحجم 8 مستخدمة في JPEG.

اقتباسات

  1. ^ أ ب ت ث ج ح خ د ذ ر ز س ش ص ض ط ظ ع غ ف ق ك ل م ن هـ و ي أأ أب أت أث Stanković, Radomir S.; Astola, Jaakko T. (2012). "Reminiscences of the Early Work in DCT: Interview with K.R. Rao" (PDF). Reprints from the Early Days of Information Sciences. 60. Retrieved 13 October 2019.
  2. ^ أ ب ت Britanak, Vladimir; Yip, Patrick C.; Rao, K. R. (2010). Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. Elsevier. pp. ix, xiii, 1, 141–304. ISBN 9780080464640.
  3. ^ أ ب ت ث Alikhani, Darya (April 1, 2015). "Beyond resolution: Rosa Menkman's glitch art". POSTmatter. Retrieved 19 October 2019.
  4. ^ أ ب ت ث ج Thomson, Gavin; Shah, Athar (2017). "Introducing HEIF and HEVC" (PDF). Apple Inc. Retrieved 5 August 2019.
  5. ^ أ ب ت ث ج ح Ahmed, Nasir; Natarajan, T.; Rao, K. R. (January 1974), "Discrete Cosine Transform", IEEE Transactions on Computers C-23 (1): 90–93, doi:10.1109/T-C.1974.223784, https://www.ic.tu-berlin.de/fileadmin/fg121/Source-Coding_WS12/selected-readings/Ahmed_et_al.__1974.pdf 
  6. ^ أ ب ت ث ج ح Rao, K. R.; Yip, P. (1990), Discrete Cosine Transform: Algorithms, Advantages, Applications, Boston: Academic Press, ISBN 978-0-12-580203-1 
  7. ^ أ ب ت ث ج ح خ Barbero, M.; Hofmann, H.; Wells, N. D. (14 November 1991). "DCT source coding and current implementations for HDTV". EBU Technical Review. European Broadcasting Union (251): 22–33. Retrieved 4 November 2019.
  8. ^ أ ب ت ث ج ح خ Lea, William (1994). "Video on demand: Research Paper 94/68". House of Commons Library. 9 May 1994. Retrieved 20 September 2019.{{cite journal}}: CS1 maint: location (link)
  9. ^ أ ب ت Ahmed, Nasir (January 1991). "How I Came Up With the Discrete Cosine Transform". Digital Signal Processing. 1 (1): 4–5. doi:10.1016/1051-2004(91)90086-Z.
  10. ^ أ ب ت ث ج ح "T.81 – Digital compression and coding of continuous-tone still images – Requirements and guidelines" (PDF). CCITT. September 1992. Retrieved 12 July 2019.
  11. ^ Britanak, Vladimir; Yip, Patrick C.; Rao, K. R. (2010). Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. Elsevier. p. 51. ISBN 9780080464640.
  12. ^ Selected Papers on Visual Communication: Technology and Applications, (SPIE Press Book), Editors T. Russell Hsing and Andrew G. Tescher, April 1990, pp. 145-149 [1].
  13. ^ Selected Papers and Tutorial in Digital Image Processing and Analysis, Volume 1, Digital Image Processing and Analysis, (IEEE Computer Society Press), Editors R. Chellappa and A. A. Sawchuk, June 1985, p. 47.
  14. ^ DCT citations via Google Scholar [2].
  15. ^ Chen, Wen-Hsiung; Smith, C. H.; Fralick, S. C. (September 1977). "A Fast Computational Algorithm for the Discrete Cosine Transform". IEEE Transactions on Communications. 25 (9): 1004–1009. doi:10.1109/TCOM.1977.1093941.
  16. ^ Smith, C.; Fralick, S. (1977). "A Fast Computational Algorithm for the Discrete Cosine Transform". IEEE Transactions on Communications. 25 (9): 1004–1009. doi:10.1109/TCOM.1977.1093941. ISSN 0090-6778.
  17. ^ Huang, T. S. (1981). Image Sequence Analysis. Springer Science & Business Media. p. 29. ISBN 9783642870378.
  18. ^ Roese, John A.; Robinson, Guner S. (30 October 1975). "Combined Spatial And Temporal Coding Of Digital Image Sequences". Efficient Transmission of Pictorial Information. International Society for Optics and Photonics. 0066: 172–181. Bibcode:1975SPIE...66..172R. doi:10.1117/12.965361.
  19. ^ Chen, Wen-Hsiung; Smith, C. H.; Fralick, S. C. (September 1977). "A Fast Computational Algorithm for the Discrete Cosine Transform". IEEE Transactions on Communications. 25 (9): 1004–1009. doi:10.1109/TCOM.1977.1093941.
  20. ^ Cianci, Philip J. (2014). High Definition Television: The Creation, Development and Implementation of HDTV Technology. McFarland. p. 63. ISBN 9780786487974.
  21. ^ أ ب ت "History of Video Compression". ITU-T. Joint Video Team (JVT) of ISO/IEC MPEG & ITU-T VCEG (ISO/IEC JTC1/SC29/WG11 and ITU-T SG16 Q.6). July 2002. pp. 11, 24–9, 33, 40–1, 53–6. Retrieved 3 November 2019.
  22. ^ أ ب ت Ghanbari, Mohammed (2003). Standard Codecs: Image Compression to Advanced Video Coding. Institution of Engineering and Technology. pp. 1–2. ISBN 9780852967102.
  23. ^ Li, Jian Ping (2006). Proceedings of the International Computer Conference 2006 on Wavelet Active Media Technology and Information Processing: Chongqing, China, 29-31 August 2006. World Scientific. p. 847. ISBN 9789812709998.
  24. ^ أ ب ت Wang, Hanli; Kwong, S.; Kok, C. (2006). "Efficient prediction algorithm of integer DCT coefficients for H.264/AVC optimization". IEEE Transactions on Circuits and Systems for Video Technology. 16 (4): 547–552. doi:10.1109/TCSVT.2006.871390.
  25. ^ Princen, John P.; Johnson, A.W.; Bradley, Alan B. (1987). "Subband/Transform coding using filter bank designs based on time domain aliasing cancellation". ICASSP '87. IEEE International Conference on Acoustics, Speech, and Signal Processing. 12: 2161–2164. doi:10.1109/ICASSP.1987.1169405.
  26. ^ John P. Princen, Alan B. Bradley: Analysis/synthesis filter bank design based on time domain aliasing cancellation, IEEE Trans. Acoust. Speech Signal Processing, ASSP-34 (5), 1153–1161, 1986
  27. ^ أ ب ت ث ج ح خ د ذ ر ز Luo, Fa-Long (2008). Mobile Multimedia Broadcasting Standards: Technology and Practice. Springer Science & Business Media. p. 590. ISBN 9780387782638.
  28. ^ أ ب Britanak, V. (2011). "On Properties, Relations, and Simplified Implementation of Filter Banks in the Dolby Digital (Plus) AC-3 Audio Coding Standards". IEEE Transactions on Audio, Speech, and Language Processing. 19 (5): 1231–1241. doi:10.1109/TASL.2010.2087755.
  29. ^ أ ب Guckert, John (Spring 2012). "The Use of FFT and MDCT in MP3 Audio Compression" (PDF). University of Utah. Retrieved 14 July 2019.
  30. ^ أ ب Brandenburg, Karlheinz (1999). "MP3 and AAC Explained" (PDF). Archived (PDF) from the original on 2017-02-13.
  31. ^ أ ب Xiph.Org Foundation (2009-06-02). "Vorbis I specification - 1.1.2 Classification". Xiph.Org Foundation. Retrieved 2009-09-22.
  32. ^ Britanak, Vladimir; Yip, Patrick C.; Rao, K. R. (2010). Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. Elsevier. pp. 35–6. ISBN 9780080464640.
  33. ^ Dhamija, Swati; Jain, Priyanka (September 2011). "Comparative Analysis for Discrete Sine Transform as a suitable method for noise estimation". IJCSI International Journal of Computer Science. 8 (Issue 5, No. 3): 162-164 (162). Retrieved 4 November 2019. {{cite journal}}: |issue= has extra text (help)
  34. ^ Mandyam, Giridhar D.; Ahmed, Nasir; Magotra, Neeraj (17 April 1995). "DCT-based scheme for lossless image compression". Digital Video Compression: Algorithms and Technologies 1995. International Society for Optics and Photonics. 2419: 474–478. Bibcode:1995SPIE.2419..474M. doi:10.1117/12.206386.
  35. ^ Komatsu, K.; Sezaki, Kaoru (1998). "Reversible discrete cosine transform". Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP '98 (Cat. No.98CH36181). 3: 1769–1772 vol.3. doi:10.1109/ICASSP.1998.681802. ISBN 0-7803-4428-6.
  36. ^ أ ب Hoffman, Roy (2012). Data Compression in Digital Systems. Springer Science & Business Media. p. 124. ISBN 9781461560319. Basically, wavelet coding is a variant on DCT-based transform coding that reduces or eliminates some of its limitations. (...) Another advantage is that rather than working with 8 × 8 blocks of pixels, as do JPEG and other block-based DCT techniques, wavelet coding can simultaneously compress the entire image.
  37. ^ Unser, M.; Blu, T. (2003). "Mathematical properties of the JPEG2000 wavelet filters" (PDF). IEEE Transactions on Image Processing. 12 (9): 1080–1090. Bibcode:2003ITIP...12.1080U. doi:10.1109/TIP.2003.812329. PMID 18237979.
  38. ^ Taubman, David; Marcellin, Michael (2012). JPEG2000 Image Compression Fundamentals, Standards and Practice: Image Compression Fundamentals, Standards and Practice. Springer Science & Business Media. ISBN 9781461507994.
  39. ^ McKernan, Brian (2005). Digital cinema: the revolution in cinematography, postproduction, and distribution. McGraw-Hill. p. 59. ISBN 978-0-07-142963-4. Wavelets have been used in a number of systems, but the technology is more processor-intensive than DCT, and it has yet to see widespread deployment.
  40. ^ Muchahary, D.; Mondal, A. J.; Parmar, R. S.; Borah, A. D.; Majumder, A. (2015). "A Simplified Design Approach for Efficient Computation of DCT". 2015 Fifth International Conference on Communication Systems and Network Technologies: 483–487. doi:10.1109/CSNT.2015.134. ISBN 978-1-4799-1797-6.
  41. ^ Chen, Wai Kai (2004). The Electrical Engineering Handbook. Elsevier. p. 906. ISBN 9780080477480.
  42. ^ Frolov, Artem; Primechaev, S. (2006). "Compressed Domain Image Retrievals Based On DCT-Processing". Semantic Scholar. Retrieved 18 October 2019.
  43. ^ أ ب ت Lee, Ruby Bei-Loh; Beck, John P.; Lamb, Joel; Severson, Kenneth E. (April 1995). "Real-time software MPEG video decoder on multimedia-enhanced PA 7100LC processors" (PDF). Hewlett-Packard Journal. 46 (2). ISSN 0018-1153.
  44. ^ أ ب ت "What Is a JPEG? The Invisible Object You See Every Day". The Atlantic. 24 September 2013. Retrieved 13 September 2019.
  45. ^ أ ب ت Pessina, Laure-Anne (12 December 2014). "JPEG changed our world". EPFL News. École Polytechnique Fédérale de Lausanne. Retrieved 13 September 2019.
  46. ^ أ ب ت Lee, Jack (2005). Scalable Continuous Media Streaming Systems: Architecture, Design, Analysis and Implementation. John Wiley & Sons. p. 25. ISBN 9780470857649.
  47. ^ أ ب ت Shishikui, Yoshiaki; Nakanishi, Hiroshi; Imaizumi, Hiroyuki (October 26–28, 1993). "An HDTV Coding Scheme using Adaptive-Dimension DCT". Signal Processing of HDTV: Proceedings of the International Workshop on HDTV '93, Ottawa, Canada. Elsevier: 611–618. doi:10.1016/B978-0-444-81844-7.50072-3. ISBN 9781483298511.
  48. ^ أ ب Ochoa-Dominguez, Humberto; Rao, K. R. (2019). Discrete Cosine Transform, Second Edition. CRC Press. pp. 1–3, 129. ISBN 9781351396486.
  49. ^ أ ب ت ث ج ح خ د ذ ر ز س ش ص ض ط ظ ع غ ف ق ك ل م ن هـ و ي أأ أب أت Ochoa-Dominguez, Humberto; Rao, K. R. (2019). Discrete Cosine Transform, Second Edition. CRC Press. pp. 1–3. ISBN 9781351396486.
  50. ^ أ ب Britanak, Vladimir; Rao, K. R. (2017). Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations. Springer. p. 478. ISBN 9783319610801.
  51. ^ أ ب Jones, Graham A.; Layer, David H.; Osenkowsky, Thomas G. (2013). National Association of Broadcasters Engineering Handbook: NAB Engineering Handbook. Taylor & Francis. pp. 558–9. ISBN 978-1-136-03410-7.
  52. ^ أ ب ت Hersent, Olivier; Petit, Jean-Pierre; Gurle, David (2005). Beyond VoIP Protocols: Understanding Voice Technology and Networking Techniques for IP Telephony. John Wiley & Sons. p. 55. ISBN 9780470023631.
  53. ^ أ ب ت ث ج Daniel Eran Dilger (June 8, 2010). "Inside iPhone 4: FaceTime video calling". AppleInsider. Retrieved June 9, 2010.
  54. ^ أ ب ت ث Blog, Netflix Technology (19 April 2017). "More Efficient Mobile Encodes for Netflix Downloads". Medium.com. Netflix. Retrieved 20 October 2019.
  55. ^ أ ب "Video Developer Report 2019" (PDF). Bitmovin. 2019. Retrieved 5 November 2019.
  56. ^ Ochoa-Dominguez, Humberto; Rao, K. R. (2019). Discrete Cosine Transform, Second Edition. CRC Press. p. 186. ISBN 9781351396486.
  57. ^ أ ب ت ث McKernan, Brian (2005). Digital cinema: the revolution in cinematography, postproduction, distribution. McGraw-Hill. p. 58. ISBN 978-0-07-142963-4. DCT is used in most of the compression systems standardized by the Moving Picture Experts Group (MPEG), is the dominant technology for image compression. In particular, it is the core technology of MPEG-2, the system used for DVDs, digital television broadcasting, that has been used for many of the trials of digital cinema.
  58. ^ أ ب Baraniuk, Chris (15 October 2015). "Copy protections could come to JPegs". BBC News. BBC. Retrieved 13 September 2019.
  59. ^ Ascher, Steven; Pincus, Edward (2012). The Filmmaker's Handbook: A Comprehensive Guide for the Digital Age: Fifth Edition. Penguin. p. 246–7. ISBN 978-1-101-61380-1.
  60. ^ Bertalmio, Marcelo (2014). Image Processing for Cinema. CRC Press. p. 95. ISBN 978-1-4398-9928-1.
  61. ^ Zhang, HongJiang (1998). "Content-Based Video Browsing And Retrieval". In Furht, Borko (ed.). Handbook of Internet and Multimedia Systems and Applications. CRC Press. pp. 83–108 (89). ISBN 9780849318580.
  62. ^ أ ب "Apple ProRes 422 Codec Family". Library of Congress. 17 November 2014. Retrieved 13 October 2019.
  63. ^ Potluri, U. S.; Madanayake, A.; Cintra, R. J.; Bayer, F. M.; Rajapaksha, N. (17 October 2012). "Multiplier-free DCT approximations for RF multi-beam digital aperture-array space imaging and directional sensing". Measurement Science and Technology. 23 (11): 114003. doi:10.1088/0957-0233/23/11/114003. ISSN 0957-0233.
  64. ^ Hudson, Graham; Léger, Alain; Niss, Birger; Sebestyén, István; Vaaben, Jørgen (31 August 2018). "JPEG-1 standard 25 years: past, present, and future reasons for a success". Journal of Electronic Imaging. 27 (4): 1. doi:10.1117/1.JEI.27.4.040901.
  65. ^ "The JPEG image format explained". BT.com. BT Group. 31 May 2018. Retrieved 5 August 2019.
  66. ^ Thomson, Gavin; Shah, Athar (2017). "Introducing HEIF and HEVC" (PDF). Apple Inc. Retrieved 5 August 2019.
  67. ^ "HEIF Comparison - High Efficiency Image File Format". Nokia Technologies. Retrieved 5 August 2019.
  68. ^ أ ب Yao Wang, Video Coding Standards: Part I, 2006
  69. ^ Yao Wang, Video Coding Standards: Part II, 2006
  70. ^ Hoffman, Roy (2012). Data Compression in Digital Systems. Springer Science & Business Media. p. 255. ISBN 9781461560319.
  71. ^ أ ب K. R. Rao and J. J. Hwang, Techniques and Standards for Image, Video, and Audio Coding, Prentice Hall, 1996; JPEG: Chapter 8; H.261: Chapter 9; MPEG-1: Chapter 10; MPEG-2: Chapter 11.
  72. ^ Davis, Andrew (13 June 1997). "The H.320 Recommendation Overview". EE Times. Retrieved 7 November 2019.
  73. ^ IEEE WESCANEX 97: communications, power, and computing : conference proceedings. University of Manitoba, Winnipeg, Manitoba, Canada: Institute of Electrical and Electronics Engineers. May 22–23, 1997. p. 30. ISBN 9780780341470. H.263 is similar to, but more complex than H.261. It is currently the most widely used international video compression standard for video telephony on ISDN (Integrated Services Digital Network) telephone lines.{{cite book}}: CS1 maint: date format (link)
  74. ^ Herre, J.; Dietz, M. (2008). "MPEG-4 high-efficiency AAC coding [Standards in a Nutshell]". IEEE Signal Processing Magazine. 25 (3): 137–142. Bibcode:2008ISPM...25..137H. doi:10.1109/MSP.2008.918684.
  75. ^ Britanak, Vladimir; Rao, K. R. (2017). Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations. Springer. p. 478. ISBN 9783319610801.
  76. ^ "Dolby AC-4: Audio Delivery for Next-Generation Entertainment Services" (PDF). Dolby Laboratories. June 2015. Retrieved 11 November 2019.
  77. ^ Bleidt, R. L.; Sen, D.; Niedermeier, A.; Czelhan, B.; Füg, S.; et al. (2017). "Development of the MPEG-H TV Audio System for ATSC 3.0" (PDF). IEEE Transactions on Broadcasting. 63 (1): 202–236. doi:10.1109/TBC.2017.2661258.
  78. ^ (October 2008) "MPEG-4 Enhanced Low Delay AAC - A New Standard for High Quality Communication" in 125th AES Convention., Audio Engineering Society. Retrieved on 20 October 2019. 
  79. ^ (May 2004) "A guideline to audio codec delay" in 116th AES Convention., Audio Engineering Society. Retrieved on 24 October 2019. 
  80. ^ أ ب Nagireddi, Sivannarayana (2008). VoIP Voice and Fax Signal Processing. John Wiley & Sons. p. 69. ISBN 9780470377864.
  81. ^ أ ب Britanak, Vladimir; Rao, K. R. (2017). Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations. Springer. pp. 31, 478. ISBN 9783319610801.
  82. ^ ITU-T SG 16 Work Programme (2005-2008) - G.718 (ex G.VBR-EV)
  83. ^ Presentation of the CELT codec by Timothy B. Terriberry (65 minutes of video, see also presentation slides in PDF)
  84. ^ Ekiga 3.1.0 available
  85. ^ FreeSWITCH: New Release For The New Year
  86. ^ (October 2013) "High-Quality, Low-Delay Music Coding in the Opus Codec" in 135th AES Convention., Audio Engineering Society. 
  87. ^ "Opus Codec". Opus (Home page). Xiph.org Foundation. Retrieved July 31, 2012.
  88. ^ Leyden, John (27 October 2015). "WhatsApp laid bare: Info-sucking app's innards probed". The Register. Retrieved 19 October 2019.
  89. ^ Hazra, Sudip; Mateti, Prabhaker (September 13–16, 2017). "Challenges in Android Forensics". In Thampi, Sabu M.; Pérez, Gregorio Martínez; Westphall, Carlos Becker; Hu, Jiankun; Fan, Chun I.; Mármol, Félix Gómez (eds.). Security in Computing and Communications: 5th International Symposium, SSCC 2017. Springer. pp. 286-299 (290). doi:10.1007/978-981-10-6898-0_24. ISBN 9789811068980.
  90. ^ Srivastava, Saurabh Ranjan; Dube, Sachin; Shrivastaya, Gulshan; Sharma, Kavita (2019). "Smartphone Triggered Security Challenges: Issues, Case Studies and Prevention". In Le, Dac-Nhuong; Kumar, Raghvendra; Mishra, Brojo Kishore; Chatterjee, Jyotir Moy; Khari, Manju (eds.). Cyber Security in Parallel and Distributed Computing: Concepts, Techniques, Applications and Case Studies. John Wiley & Sons. pp. 187–206 (200). doi:10.1002/9781119488330.ch12. ISBN 9781119488057. {{cite book}}: |journal= ignored (help)
  91. ^ "Open Source Software used in PlayStation®4". Sony Interactive Entertainment Inc. Retrieved 2017-12-11.
  92. ^ "Enhanced Voice Services (EVS) Codec" (PDF). Fraunhofer IIS. March 2017. Retrieved 19 October 2019.
  93. ^ Abousleman, G. P.; Marcellin, M. W.; Hunt, B. R. (January 1995), "Compression of hyperspectral imagery using 3-D DCT and hybrid DPCM/DCT", IEEE Trans. Geosci. Remote Sens. 33 (1): 26–34, doi:10.1109/36.368225, Bibcode: 1995ITGRS..33...26A 
  94. ^ Chan, Y.; Siu, W. (May 1997), "Variable temporal-length 3-D discrete cosine transform coding", IEEE Trans. Image Processing. 6 (5): 758–763, doi:10.1109/83.568933, PMID 18282969, Bibcode: 1997ITIP....6..758C, http://www.en.polyu.edu.hk/~wcsiu/paper_store/Journal/1997/1997_J3-IEEE-Chan%26Siu.pdf 
  95. ^ Song, J.; SXiong, Z.; Liu, X.; Liu, Y., "An algorithm for layered video coding and transmission", Proc. Fourth Int. Conf./Exh. High Performance Comput. Asia-Pacific Region 2: 700–703 
  96. ^ Tai, S.-C; Gi, Y.; Lin, C.-W. (September 2000), "An adaptive 3-D discrete cosine transform coder for medical image compression", IEEE Trans. Inf. Technol. Biomed. 4 (3): 259–263, doi:10.1109/4233.870036, PMID 11026596 
  97. ^ Yeo, B.; Liu, B. (May 1995), "Volume rendering of DCT-based compressed 3D scalar data", IEEE Trans. Comput. Graphics. 1: 29–43, doi:10.1109/2945.468390 
  98. ^ CHAN, S.C., LlU, W., and HO, K.L.: ‘Perfect reconstruction modulated filter banks with sum of powers-of-two coefficients’. Proceedings of Inte.n Symp. Circuits and syst., 28-3 1 May 2000, Geneva, Switzerland, pp. 28-31
  99. ^ Queiroz, R. L.; Nguyen, T. Q. (1996). "Lapped transforms for efficient transform/subband coding". IEEE Trans. Signal Process. 44 (5): 497–507.
  100. ^ Malvar, H. S. (1992). Signal processing with lapped transforms. Englewood Cliffs, NJ: Prentice Hall.
  101. ^ Chan, S. C.; Luo, L.; Ho, K. L. (1998). "M-Channel compactly supported biorthogonal cosine-modulated wavelet bases". IEEE Trans. Signal Process. 46 (2): 1142–1151. Bibcode:1998ITSP...46.1142C. doi:10.1109/78.668566. hdl:10722/42775.
  102. ^ أ ب Katsaggelos, Aggelos K.; Babacan, S. Derin; Chun-Jen, Tsai (2009). "Chapter 15 - Iterative Image Restoration". The Essential Guide to Image Processing. Academic Press. pp. 349–383. ISBN 9780123744579.
  103. ^ "Mosquito noise". PC Magazine. Retrieved 19 October 2019.
  104. ^ Menkman, Rosa (October 2011). The Glitch Moment(um) (PDF). Institute of Network Cultures. ISBN 978-90-816021-6-7. Retrieved 19 October 2019.
  105. ^ jpegs, Thomas Ruff, Aperture, May 31, 2009, 132 pp., ISBN 978-1-59711-093-8
  106. ^ Review: jpegs by Thomas Ruff, by Jörg Colberg, April 17, 2009
  107. ^ "Discrete cosine transform - MATLAB dct". www.mathworks.com. Retrieved 2019-07-11.
  108. ^ W. B. Pennebaker and J. L. Mitchell, JPEG Still Image Data Compression Standard. New York: Van Nostrand Reinhold, 1993.
  109. ^ Y. Arai, T. Agui, and M. Nakajima, “A fast DCT-SQ scheme for images,” Trans. IEICE, vol. 71, no. 11, pp. 1095–1097, 1988.
  110. ^ X. Shao and S. G. Johnson, “Type-II/III DCT/DST algorithms with reduced number of arithmetic operations,” Signal Processing, vol. 88, pp. 1553–1564, June 2008.
  111. ^ Malvar 1992
  112. ^ Martucci 1994
  113. ^ S. C. Chan and K. L. Ho, “Direct methods for computing discrete sinusoidal transforms,” in Proc. Inst. Elect. Eng. Radar Signal Process., vol. 137, Dec. 1990, pp. 433–442.
  114. ^ أ ب O. Alshibami and S. Boussakta, “Three-dimensional algorithm for the 3-D DCT-III,” in Proc. Sixth Int. Symp. Commun., Theory Applications, July 2001, pp. 104–107.
  115. ^ G. Bi, G. Li, K.-K. Ma, and T. C. Tan, “On the computation of two-dimensional DCT,” IEEE Trans. Signal Process., vol. 48, pp. 1171–1183, Apr. 2000.
  116. ^ E. Feig, “On the multiplicative complexity of discrete \cosine transforms,”IEEE Trans. Inf. Theory, vol. 38, pp. 1387–1390, Aug. 1992.
  117. ^ Nussbaumer, H. J. (1981). Fast Fourier transform and convolution algorithms (1st ed.). New York: Springer-Verlag.
  118. ^ قالب:Cite بيانات حقيقيةjournal

Further reading

وصلات خارجية

الكلمات الدالة:
تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=تحويل_جيب_التمام_المتقطع&oldid=2367500"