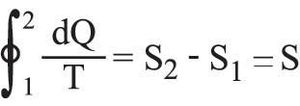عشوائية داخلية

معادلات ثرموديناميكية
علاقات ماكسويل
معادلة گيبس-دوهم
معادلة فان در ڤالز
علاقة کلاوزیوس-کلاپیرون
معادلات بريدجمان

Ice melting is a common example of "entropy increasing" described in 1862 by Rudolf Clausius as an increase in the disgregation of the molecules of the body of ice.

الإنتروپيا او الاعتلاج (إنگليزية: entropy) – عادة ً مرموزة بالحرف S – تعبـّر عن مدى العشوائية الداخلية خلال الجزيئات في داخل نظام فيزيائي.

بـاِختلاف من الإنتروپيا أو الاعتلاج العشوائية الداخلية «لا» تملك وحدة فيزيائية. عكساً من ذلك الإنتروپيا (أو الاعتلاج) تملك وحدة فيزيائية. جملة الواحدات الدولية تقدر الإنتروپيا بالجول لكل كلفن (J·K⁻¹) ، حيث تعتبر الإنتروپيا متغيـّرة مـُقـْتـَرَنـَة (conjugate variable) لدرجة الحرارة . بالإضافة إلى ذلك العشوائية الداخلية هي غير قابلة للقياس. العشوائية الداخلية خلال الجزيئات في داخل نظام تعتبر مفهوم مساعد لاِستيعاب نماذج معيـّنة تـُسـْتـَعـْمـَل في الثرموديناميكا، وهي تدعم فهم الإنتروپيا في التصوّر الإنساني. لا أكثر.

ويمكن القول بأن الإنتروپيا تعتبر وصف هامّ لأنظمة ثرموديناميكية عندما تكون في ظروف عدم التوازن. في الديناميكا الحرارية و الميكانيكا الإحصائية ، تشكل الإنتروپيا متغيرا فيزيائيا أساسيا لوصف نظام ثرموديناميكي (أنظر التفاصيل لاحقاً).

رودلف كلاوزيوس, مبدع مفهوم الإنتروپيا

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 نبذة من الأسس

تعتمد الإنتروپيا فقط على الحالة الراهنة للنظام الثرموديناميكي ، و ليس على تاريخه التفصيلي ، أي أنه دالة حالة state function للمؤشرات الثرموديناميكية مثل الضغط و درجة الحرارة ، .. الخ ، التي تصف الخواص المجهرية المقيسة للنظام .

يوجد ارتباط مهم بين الإنتروپيا و مقدار الطاقة الداخلية في النظام التي لا يمكن تحويلها لشغل . ففي أي عملية عندما يعطي النظام طاقة بمقدار ΔE ، و تنخفض إنتروپياه بمقدار ΔS فإن مقدارا T_R ΔS من هذه الطاقة على الأقل يجب أن يذهب لمحيط النظام بشكل حرارة غير قابلة للاستعمال ، و إلا فإن العملية لن تستمر . (T_R هي حرارة المحيط الخارجي للنظام، الذي لا يمكن ان يكون بنفس درجة حرارة النظام T ).

وفق المبكانيك الإحصائي ، حسب بولتزمان تعتبر الإنتروپيا مقياس لإحتمال حالة فزيائية معينة. و قد صاغ ذلك في القانون التالي:

$S=k\cdot lnW$

حيث k هي ثابت بولتزمان و تساوي $1,380662.10^{-23}J/K$ و W هي احتمال حدوث حالة ثرموديناميكية. تعتبر فكرة العشوائية الداخلية أساس القانون الثاني للديناميكا الحرارية. وطبقًا لهذا القانون فإن اتجاه التغير التلقائي في الأنظمة المعزولة يكتنفه اختلال أكبر. لذلك تنتقل الحرارة تلقائيًا فقط من المواد الساخنة إلى مواد باردة. وعندما تكتسب المواد الباردة الحرارة تصبح حركة جزيئاتها أكثر اختلالاً ويزداد تحولها الداخلي. انظر: الحرارة.

وبالإضافة إلى ذلك يتمدد الغاز دائمًا لملء وعائه، حيث تزداد العشوائية الداخلية للغاز كلما تمدد، وذلك لتوافر أماكن كثيرة للجزيئات. ولكل مادة عشوائية داخلية أكبر بوصفها غاز مقارنة بعشوائيتها الداخلية بوصفها سائل.

وربما تحدث بعض التغيرات انخفاضًا في العشوائية الداخلية في أحد الأنظمة، لكن هذا الانخفاض يمكن تعويضه من زيادة العشوائية الداخلية في الأنظمة المتصلة. فعلى سبيل المثال تنخفض العشوائية الداخلية للماء كلما تجمد السائل، لكن الحرارة المنطلقة في العملية تزيد العشوائية الداخلية للهواء المحيط.

وتزداد العشوائية الداخلية للمادة عندما تفقد المادة بعض قدرتها على الشغل. فالهواء المدخل إلى بالون فارغ، على سبيل المثال له إنتروپيا منخفضة لأن جزيئات الهواء مضغوطة في حيّز صغير. ويبذل الهواء المضغوط شغلاً بالتمدد ونفخ البالون. وفي البالون المنفوخ تستطيع الجزيئات أن تشغل عددا أكبر من الأماكن، وبالتالي يكون لها إنتروپيا أكبر. لكن هذه الجزيئات تكون قد فقدت القدرة على المزيد من العمل عند تضخيم البالون أكثر.

ولو أخذنا جميع العمليات التي تحدث الآن، فسوف ينتج عنها كون من الاختلال الكبير. ولأن العشوائية الداخلية للكون في ارتفاع مستمر، فإن حالة الإنتروپيا الكبيرة هذه يجب أن تحدث في وقت لاحق، ولهذا السبب يشار إلى الإنتروپيا أحيانًا بالسهم الزمني.

 التحولات العكوسة

لقد لوحظ أن الجملة الموجودة في شروط خارجية ثابتة تتحول مقتربةً من حالة نهائية بسيطة تسمى حالة التوازن. فمثلاً، إذا وُصِل جسمان مختلفان في درجتي حرارتيهما بسلك معدني، انتقلت الحرارة من الجسم الساخن إلى الجسم البارد حتى تتساوى درجتا الحرارة في الجسمين. كذلك إذا وُصِل وعاء يحوي غازاً عبر صنبور بوعاءٍ مُخلّى من الهواء، فإن الغاز يتمدد ويستمر تمدّده حتى يمتلئ كلا الوعاءين امتلاءً منتظماً. كما يمكن أن يمتزج غازان امتزاجاً تاماً مع تساوي درجة الحرارة والضغط فيهما.

إن هذه التحولات وأمثالها مألوفة، إلا أن التحولات المعاكسة غير مألوفة، ولا يمكن إجراؤها تجريبياً من دون تدخل الوسط الخارجي. فلم يُلاحظ قط انتقال الحرارة من جسم بارد إلى جسم ساخن، ولا انضغاط غازٍ تلقائياً ليملأ أحد الوعاءيْن، ولا انفصال أحد الغازيْن الممتزجين عن الآخر تلقائياً. وقد صنّف ماكس پلانك Planck كل التحولات الأولية في ثلاثة أصناف: طبيعية وغير طبيعية وعكوسة.

فالتحولات الطبيعية هي تحولات تلقائية تحدث في اتجاه التوازن. أما التحولات غير الطبيعية فهي التي لا تحدث مطلقاً لابتعادها عن حالة التوازن. فمثلاً، إذا كان التحول أ!ب طبيعياً، كان التحول ب!أ غير طبيعي. أما التحول العكوس فهو تحول طبيعي مثالي يمر بسلسلة متصلة من حالات التوازن، مثال ذلك تبخّر سائل بوجود بخاره في الضغط P، فإذا افتُرض أن ضغط البخار التوازني للسائل يساوي p، فإن السائل يتبخر بتحول طبيعي إذا كان P < p؛ أما إذا كان P > p، فإن التحول يكون غير طبيعي ولا يحدث؛ وما يحدث فعلاً حينئذ هو التحول المعاكس، وهو تكاثف البخار condensation. وإذا كان p = P، فإن عمليتي التبخر والتكاثف تكونان عكوستين، ويمكن أن تبدأ أيٌ منهما بزيادة بسيطة في الضغط الخارجي P، أو بنقصان طفيف فيه. فالتحول العكوس يمكن إذن عكسه عكساً تاماً بتغييرٍ في الشروط الخارجية لا متناه في الصغر. فإذا جُعل جسم في جوار جسم أبرد منه كثيراً، فإنه لا يمكن عكس اتجاه جريان الحرارة بإحداث تغيير طفيف في درجة حرارة أحد الجسمين. أما في التحول العكوس فيتم التحول بإحداث تغيرات طفيفة في فروق الضغط، ويتم انتقال الحرارة بإحداث فروق ضئيلة في درجة الحرارة.

 دالة الإنتروپيا

عندما تقوم جملة ترموديناميكية بدورة تحولات قابلة للانعكاس وفق مبدأ كارنو Carnot فإن العلاقة التالية:

تصح من أجل دورة ثنائية درجة الحرارة ditherm، حيث T₁، T₂ درجتا الحرارة المطلقتان لمنبعي الحرارة اللذين هما على تماس مع الجملة التي تتبادل معهما كميتي الحرارة Q₁، Q₂ المحسوبتين جبرياً. وتتحقق العلاقة :

في حالة دورة عكوسة ما لجملةٍ هي على تماس متعاقب مع عددٍ كبير من المنابع الحرارية في درجات حرارة مختلفة، أي إن:

حيث dQ: كمية الحرارة التي تتلقاها الجملة من المنبع ذي الدرجة T. أما إذا كان التحول مفتوحاً، فإن الجملة تنتقل من حالة ابتدائية (1) إلى حالة نهائية (2) ، ويُبرهن بسهولة على أن الكمية

مستقلة عن الطريق المسلوكة، ولا تتوقف إلا على الحالتين الابتدائية والنهائية. وعلى هذا يمكن، في حالة هذه الجملة، تعريف دالةٍ لمقادير تُميِّز حالة هذه الجملة، أو يمكن بعبارة أخرى تعريف دالة حالةٍ بحيث يكون :

إن هذه الدالة S، التي لم تُعرَّف هنا إلا بتقريب ثابتةٍ اختيارية، هي بالتعريف إنتروپيا الجملة المعتبرة.

وفي حالة تحولٍ عكوس لا متناهٍ في الصغر يكون:

وفي الحالة الخاصة لتحول متساوي الدرجة isotherm، في الدرجة T (كلفن) يكون:

حيث Q: كمية الحرارة التي تتلقاها الجملة. وتُعدّ هذه الكمية موجبة عندما تتلقاها الجملة فعلياً. وينتج من هذا أن الجملة تزداد إنتروپياها عندما تمتص الحرارة. أما إذا لم تتبادل الجملة مع المحيط الخارجي حرارة خلال تحول عكوس فإن إنتروپياها لا تتغير، ويقال حينئذ إن التحول متساوي الإنتروپيا isentropie.

إن حساب تغير الإنتروپيا لجملة بين حالتين يعدّ حساباً سهلاً في حالة غاز كامل. فإذا أُخذ مول واحد من الغاز الكامل فإنه ينتج من تعريف المعاملات الترموديناميكية إمكان كتابة ما يلي في حالة تحول عكوس لا متناه في الصغر:

نظراً لكون الغاز كاملاً، وحيث CV السعة الحرارية المولية للغاز في حجم ثابت، وR ثابت الغازات الكاملة.

وعلى هذا تتغير درجة حرارة الغاز من T0 إلى T في حالة تحول محدَّد عكوس، ويتغير الحجم من V0 إلى V، ويكون:

فإذا افتُرض، بغية التبسيط، أن CV ثابتة، فإنه ينتج أن:

وفي حالة تغير في الضغط تصبح العلاقة على النحو التالي:

إن العلاقة (1) تصبح في حالة تحول قابل للانعكاس متساوي الحجم كما يلي:

وهذا الازدياد في إنتروپيا الجسم يكافئه، بسبب عكوسية التحول النقصانُ الكلي في إنتروپيا المنبعين، إذ إن درجة حرارة الجسم في كل لحظة تساوي درجة حرارة المنبع الذي يكون الجسم على تماس معه. أما في حالة التحول اللاعكوس فيكون ازدياد الأنتروبية هو أيضاً:

ولكن نقصان إنتروپيا المنبع ذي الدرجة T₂، الذي يغذّي الجسم بكمية الحرارة المعطاة بـ:

Q = C_V(T₁-T₂)

يساوي:

ومن السهل تبيُّن أن:

فالجسم اكتسب إنتروپيا أكثر من تلك التي خسرها المنبع. ولما لم يكن هناك أي تبادل حراري آخر، فإنه يُستنتج أن كمية معينة من الإنتروپيا قد تولَّدت في هذا التحول التلقائي. فعند النظر في جملةٍ تشتمل على الجسم السابق والمنبعين، تكون التبادلات السابقة تبادلات داخلية (أي في الجملة)، ولا يعدِّل التحولُ الداخلي العكوس الإنتروپيا الكلية للجملة، في حين يولّد التحول التلقائي زيادة فيها. وقد أدت هذه النتيجة إلى قبول المسلَّمة التالية: «تزداد أنتروبية الجملة المعزولة في حالة كل تحول تلقائي يطرأ عليها، في حين تظل ثابتة في كل تحول عكوس؛ ولا يمكن لها أن تنقص ما دامت الجملة معزولة». إن التوازن المستقر لجملة معزولة يحدث عندما تصبح قيمة أنتروبيتها عظمى، ولا يمكن للإنتروپيا بعد ذلك أن تتطور. إن هذا الافتراض السابق يكوِّن نص القانون الثاني في التحريك الحراري (الترموديناميك)، المنسوب إلى كلاوسيوس Clausius. يستحيل تحقيق تحولٍ تكون نتيجته الوحيدة أخذ كمية حرارة من خزان وحيد وتحويلها إلى عملٍ يكافئها.

 مفهوم الإنتروپيا الفيزيائي

وُصفت الأنتروبية بأنها مفهوم مجرد إلى حد بعيد، ووصف هذا المفهوم بأنه أقل وضوحاً من المفاهيم الميكانيكية كالقوة أو التسارع أو الطاقة، بل إنه أقل وضوحاً من مفهوم درجة الحرارة أو كمية الحرارة. ويرجع السبب في ذلك إلى أن مثل هذه المفاهيم الفيزيائية إما أن تكون فيسيولوجية المنشأ أو أن تكون على صلة وثيقة بالمفاهيم الفيزيولوجية المنشأ.

 مفهوم الإنتروپيا باستخدام مفهوم الطاقة

ومع ذلك يمكن تقريب مفهوم الإنتروپيا باستخدام مفهوم الطاقة: إن كل نوع من أنواع الطاقة يمكن التعبير عنه رياضياً بجداء عاملين مثل جداء القوة بالانتقال F.dl أو جداء الثقل بالارتفاع W.dh في حالة الطاقة الميكانيكية؛ أو جداء الحقل الكهربائي بالشحنة E.dq في حالة الطاقة الكهربائية؛ أو جداء الضغط بالحجم P.dv في حالة طاقة الضغط؛ أو جداء درجة الحرارة بتغير الإنتروپيا T.ds في حالة الطاقة الحرارية. ويتألف كلٌ من هذه الجداءات من عامليْن، أحدهما هو متغيُر توترٍ (شدة)، مثل: (القوة والوزن والحقل الكهربائي والضغط أو درجة الحرارة) وهو يعبِّر عن حالة التوازن. أما العامل الثاني فهو عامل كمية ويتناسب مع كِبر الجملة مثل: extension التمدد والطول وكمية الكهرباء والحجم والإنتروپيا. فمثلاً عندما يقاس متغير توتر كالضغط أو درجة الحرارة في جملة متوازنة، فإن مقداره يكون ثابتاً ولا يتوقف على موضعه أو كِبَر الجملة. إن للمقادير الامتدادية extension خواص جمعية، وتتصف جميعها تقريباً بأنها تخضع لمبدأ الانحفاظ conservation، فلا يمكن مثلا توليد كمية كهربائية أو إفناؤها، أما الإنتروپيا فهي وحدها المستثناة، إذ إنها تشذ عن هذا المبدأ، فمع استحالة إفنائها فإن بالإمكان توليدها؛ وهذا الإمكان هو السبب في شذوذ الإنتروپيا عن مختلف المقادير الامتدادية الأخرى، وهو السبب أيضاً في شذوذ الطاقة الحرارية عن مختلف الطاقات الأخرى.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انحطاط الطاقة degradation of energy

تبقى الطاقة محفوظة في أي تحوّل سواء أكان التحول قابلاً للانعكاس أم كان غير قابل له؛ ولكن شيئاً غير الطاقة يكون مفقوداً في التحول، فمثلاً في تجربة جول تتحول الطاقة الميكانيكية إلى طاقة حرارية يكتسبها الماء وتستقر فيه، وإذا أُريد استخدام هذه الطاقة الحرارية فإنها تتحول إلى عمل أقل كثيراً مما صُرف لتوليدها. فالطاقة الأولى انحطت إلى شكل أقل نفعاً ومردوداً. كذلك إذا امتزج ماء بارد بماء ساخن تكون الطاقة الداخلية للجملة واحدة قبل المزج وبعده وفقاً لمبدأ انحفاظ الطاقة. ولكن يكون هناك بعد المزج خزان واحد في درجة حرارة واحدة؛ في حين كان الماء قبل المزج في خزانين في درجتي حرارة مختلفتين. ومن المستحيل وفقا للمبدأ الثاني في التحريك الحراري تحويل الحرارة إلى عمل ميكانيكي من خزان وحيد، في حين كان من الممكن فعل ذلك باستخدام الخزان الساخن الأول مع خزانات أخرى باردة، وتحويل جزءٍ من الحرارة إلى عمل. فالطاقة الداخلية للجملة قبل المزج انحطت إلى شكل أقل نفعاً ومردوداً، ويحدث الأمر في أي تحول طبيعي لاعكوس. وعلى هذا يمكن أن تعدَّ الإنتروپيا مقياساً لمدى الاستفادة من الطاقة. وإذا كانت طاقة الكون محفوظة فإن إنتروپياه تسعى نحو نهاية عظمى.

 تعيين القيمة المطلقة للإنتروپيا

إن معرفة قيم إنتروپيا الأجسام بدلالة درجة الحرارة والضغط مهمة جداً لتحديد إمكانات التفاعلات الكيمياوية، فهي لا تكون ممكنة إلا إذا أدى التفاعل إلى تزايد الإنتروپيا في التحول اللاعكوس. ولكن إنتروپيا جسم في حالة معينة لا تكون معروفة إلا بتقريب ثابتة اختيارية وفقاً للعلاقة:

ولتعيين القيمة المطلقة للإنتروپيا وُضعت فرضية معروفة باسم فرضية نرسنت بلانك Nernst-Planck، اعتماداً على تجارب أُجريت في درجات حرارة منخفضة جداً حُدِّدت فيها قيم هذه الثابتة بالقول: إن إنتروپيا جميع الأجسام تؤول إلى الصفر عندما تؤول درجة الحرارة إلى درجة الصفر المطلق (التي لم تبلغها التجارب)، وتؤلف هذه الفرضية المبدأ الثالث في التحريك الحراري التقليدي. وقد أُدرجت في جداول الثوابت العددية قيمُ أنتروبية الأجسام المختلفة، بدءاً من درجة الصفر المطلق؛ وقد تم الحصول عليها بقياسات حرارية في الشرطين T=298K، و1=P جو وهذه القيم تفيد في تطبيقات كثيرة في التفاعلات الكيمياوية وفي الهندسة الميكانيكية.

 الإنتروپيا والاحتمال

يحتم المبدأ الثاني في التحريك الحراري استحالة انفصال ذرات الغاز السريعة عن الذرات البطيئة الموجودة في أسطوانة، لأن هذا الانفصال هو تحول مصحوب بنقصان إنتروپيا الجملة. ولكن الحركة العشوائية الدائمة لذرات الغاز قد تؤدي إلى تصور احتمال تجمع الذرات السريعة في مكان ما من الأسطوانة، غير أن احتمال وقوع هذه الحادثة ضعيف جداً لأنه لم يلاحظ حتى اليوم مثل هذا التحول. وهذا هو ما تدل عليه نظرية الاحتمال التي تبين أن احتمال انفصال الذرات السريعة عن الذرات البطيئة انفصالاً تاماً يساوي (1/2)ⁿ، حيث n: عدد ذرات الغاز. فإذا كان هناك ذرة غرامية واحدة من الغاز، كان N=n (عدد آفوغادرو) 6ײ³10، فإن الاحتمال في هذه الحالة يساوي الصفر عملياً. إن هذا الارتباط غير المباشر ما بين الإنتروپيا والاحتمال يمكن تبيينه بتطبيق العلاقة (1) على تحول عكوس متساوي درجة الحرارة، فيكون تغير الإنتروپيا مساوياً:

حيث V0: حجم الغاز الابتدائي، وV= حجمه في نهاية التحول. أما احتمال وجود ذرة ما من الغاز في جزءٍ ما V من الأسطوانة ذات الحجم V0 فيساوي نسبة مجموع الحالات المواتية favorable لوقوع ذلك إلى مجموع الحالات الممكنة، أي يساوي

وأما احتمال وجود ذرات الغاز كلها التي عددها N (في حالة ذرة غرامية) في الجزء V فقط فيساوي أيضاً

بتعويض هذه العلاقة في (3) يصبح تغير الإنتروپيا:

أو:

حيث k: ثابت ستيفان-بولتزمان Boltzmann وتساوي 1.381× 10^-23 جول/كلفن وحيث C: ثابتة اختيارية هي كالثابتة الاختيارية التي تدخل في تعيين دالة الإنتروپيا. وتدل العلاقة (4) على أن أنتروبية جملة ما تبلغ قيمة عظمى في حالتها الأكثر احتمالاً، وهذا ما يتفق مع مبدأ تزايد الإنتروپيا.

وتجدر الإشارة أخيراً إلى أن عبارة الإنتروپيا أُدخلت في نظرية المعلومات بصيغة شبيهة بالعلاقة (4) لتدل على قياس المعلومات المتاحة (المحتملة) في جملةٍ من الجمل.

 انظر أيضا

• سهم الزمن Arrow of time
• ثقب أسود Black hole
• قوة اعتلاجية Entropic force
• إنتروپيا المزج Entropy of mixing
• إنتروپيا المعلومات Information entropy
• إنتروپيا كولموغوروف-سيناي Kolmogorov-Sinai entropy (في الجمل الحركية)
• وحدات لوغاريثمية Logarithmic units
• عفريت ماكسويل Maxwell's demon
• إنتروپيا متبقية Residual entropy
• كمون ترمودينامي Thermodynamic potential
• Negentropy
• Ectropy

 مراجع

الموسوعة المعرفية الشاملة

• P. Pluch Quantum Probability Theory, PhD Thesis, University of Klagenfurt (2006)

 قراءات أخرى

1. Ben-Naim, Arieh (2007). Entropy Demystified. World Scientific. ISBN 981-270-055-2.
2. Dugdale, J. S. (1996). Entropy and its Physical Meaning (2nd Ed. ed.). Taylor and Francis (UK); CRC (US). ISBN 0748405690. {{cite book}}: |edition= has extra text (help)
3. Fermi, Enrico (1937). Thermodynamics. Prentice Hall. ISBN 0-486-60361-X.
4. Kroemer, Herbert (1980). Thermal Physics (2nd Ed. ed.). W. H. Freeman Company. ISBN 0-7167-1088-9. {{cite book}}: |edition= has extra text (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
5. Penrose, Roger (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. ISBN 0-679-45443-8.
6. Reif, F. (1965). Fundamentals of statistical and thermal physics. McGraw-Hill. ISBN 0-07-051800-9.
7. Goldstein, Martin; Inge, F (1993). The Refrigerator and the Universe. Harvard University Press. ISBN 0-674-75325-9.{{cite book}}: CS1 maint: multiple names: authors list (link)
8. vonBaeyer; Hans Christian (1998). Maxwell's Demon: Why Warmth Disperses and Time Passes. Random House. ISBN 0-679-43342-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
9. Entropy for beginners

1. عبد الله واثق شهيد، الترموديناميك (جامعة دمشق 1968).
2. الفيزياء الإحصائية، ترجمة بغدادي ودرويش وعوض (مطبعة جامعة دمشق).
3. F.W.SEARS, Thermodynamics (1963).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

• Entropy - A Basic Understanding A primer for entropy from a chemical perspective
• Interactive Shockwave Animation on Entropy
• Max Jammer (1973). Dictionary of the History of Ideas: Entropy
• Frank L. Lambert; entropysite.com – links to articles including simple introductions to entropy for chemistry students and for general readers.
• Thermodynamics - a chapter from an online textbook
• Entropy on Project PHYSNET
• Entropy - an Open Access journal