مدار إهليلجي

تحريك لرسم مسار الدوران باختلاف المراكز
0.0 • 0.2 • 0.4 • 0.6 • 0.8

جرمان بكتلة مماثلة يدوران حول مركز ثقل مشترك بمدارات إهليلجية.

جرمان بكتلة غير متساوية يدوران حول مركز ثقل مشترك بمدارات دائرية.

جرمان بكتلة غير متساوية بشكل كبير يدوران حول مركز ثقل مشترك بمدارات دائرية.

صُور مدار بيضاوي في الربع العلوي الأيمن من هذا الرسم البياني، حيث يُظهر الحفرة الجاذبية للكتلة المركزية الطاقة المحتملة، وتُظهر الطاقة الحركية لسرعة المدار باللون الأحمر. ينخفض ارتفاع الطاقة الحركية مع انخفاض سرعة الجرم المداري وزيادة المسافة وفقاً لقوانين كپلر.

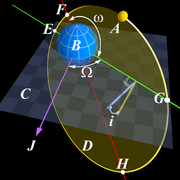في علم الديناميكا الفلكية أو الميكانيكا السماوية، مدار إهليلجي أو المدار البيضاوي إنگليزية: Elliptic orbit هو مدار كبلري مع انحراف أقل من واحد؛ ويشمل هذا الحالة الخاصة للمدار الدائري، حيث يكون الانحراف مساوياً للصفر. بمعنى أدق، هو مدار كبلري بقيمة للانحراف تزيد عن الصفر وتقل عن واحد (وبالتالي يستبعد المدار الدائري). بمعنى أوسع، هو مدار كبلري بطاقة سالبة. ويشمل هذا المدار المباشر اإهليلجي، حيث يكون الانحراف مساوياً للواحد.

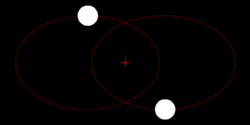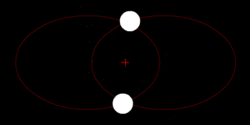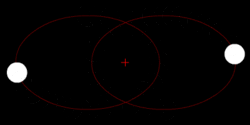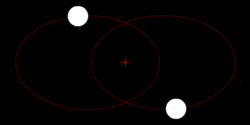
في مسألة الجاذبية ثنائية الأجسام ذات الطاقة السالبة، يتبع كلا الجرمين مدار إهليلجي مشابه بنفس الدور المداري حول مركز الجاذبية المشترك بينهما. أيضاً، تتبع الوضع النسبي لجرم واحد بالنسبة للجسم الآخر مدار إهليلجي.

أمثلة على المدارات الإهليلجية تشمل: مدار هوهمان الانتقالي (Hohmann transfer orbit)، مدار مولنيا (Molniya orbit)، ومدار التندرا (Tundra orbit).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

السرعة

بالافتراضات القياسية، وعدم وجود قوى أخرى تعمل إلا الجرمين المتجانسين كروياً m₁ وm₂^[1]يمكن حساب السرعة المدارية ( $v\,$ ) للجرم الذي ينتقل على مدار إهليلجي من معادلة فيس-فيفا (vis-viva equation) على النحو التالي:^[2]

v={\sqrt {\mu \left({2 \over {r}}-{1 \over {a}}\right)}}

حيث:

معامل الجاذبية القياسي $\mu \,$ هو حاصل ضرب الثابت الجاذبي G(m₁+m₂) (في مجموع كتلتي الجرمين m1 وm2)، وعادة ما يعبر عنه بـ GM عندما يكون أحد الجرمين أكبر بكثير من الآخر.
$r\,$ هي المسافة بين الجرم المداري ومركز الكتلة.
$a\,\!$ هي طول نصف المحور الرئيسي.

معادلة السرعة للمسار الزائدي الناقص تحتوي إما على + ${1 \over {a}}$ أو تكون نفسها بافتراض أن a سالبة في هذه الحالة.

الفترة المدارية

وفق الافتراضات القياسية، يمكن حساب فترة المدار ( $T\,\!$ ) لجرم يتحرك على مدار إهليلجي كما يلي:^[3]

T=2\pi {\sqrt {a^{3} \over {\mu }}}

حيث:

$\mu$ وهي بارامتر الجاذبية القياسية.
$a\,\!$ هو طول نصف المحور الرئيسي.

نستنتج:

فترة المدار تساوي تلك الخاصة بمسار دائري مع نصف قطر المدار يساوي نصف المحور الرئيسي ( $a\,\!$ ),
بالنسبة لنصف المحور الرئيسي المحدد، لا تعتمد فترة المدار على الاختلاف المركزي. (انظر: قانون كبلر الثالث).

الطاقة

وفقاً للافتراضات القياسية، تكون الطاقة المدارية النوعية ( $\epsilon$ ) لـ مدار إهليلجي سالبة ويمكن أن تأخذ معادلة حفظ الطاقة المدارية (Vis-viva equation) لهذا المدار الشكل:^[4]

{v^{2} \over {2}}-{\mu  \over {r}}=-{\mu  \over {2a}}=\epsilon <0

حيث:

$v\,$ هو السرعة المدارية للجرم المداري،
$r\,$ هو مسافة الجرم المداري من الجسم المركزي،
$a\,$ هو طول نصف المحور الرئيسي،
$\mu \,$ هي بارامتر الجاذبية القياسية.

باختصار:

لمحور شبه رئيسي معين، تكون الطاقة المدارية النوعية مستقلة عن الاختلاف المركزي.

باستخدام نظرية فيريال نجد:

متوسط الطاقة النوعية على مدار الزمن يساوي −2ε
- متوسط قيمة الزمن r⁻¹ هو a⁻¹.
متوسط الوقت للطاقة الحركية المحددة يساوي ε

الطاقة من حيث نصف المحور الرئيسي

من المفيد معرفة الطاقة من حيث نصف المحور الرئيسي (والكتل المعنية). تعطى الطاقة الكلية للمدار بواسطة

E=-G{\frac {Mm}{2a}}

,

حيث a هو نصف المحور الرئيسي.

الاستنتاج

نظراً لأن الجاذبية قوة مركزية، فإن الزخم الزاوي ثابت:

{\dot {\mathbf {L} }}=\mathbf {r} \times \mathbf {F} =\mathbf {r} \times F(r)\mathbf {\hat {r}} =0

في أقرب وآخر نهج، يكون الزخم الزاوي عمودياً على المسافة من الكتلة المدارية، لذلك:

L=rp=rmv

.

الطاقة الكلية للمدار تعطى بواسطة^[5]

E={\frac {1}{2}}mv^{2}-G{\frac {Mm}{r}}

.

يمكننا استبدال v والحصول على

E={\frac {1}{2}}{\frac {L^{2}}{mr^{2}}}-G{\frac {Mm}{r}}

.

صحيح بالنسبة لـ r هو أقرب/أبعد مسافة، لذلك نحصل على معادلتين متزامنتين نحلهما بالنسبة إلى E:

E=-G{\frac {Mm}{r_{1}+r_{2}}}

اعتباراً ${\textstyle r_{1}=a+a\epsilon }$ و $r_{2}=a-a\epsilon$ ، عندما يكون إبسيلون هو الانحراف اللامركزي للمدار، فقد حصلنا أخيراً على النتيجة المعلنة.

زاوية مسار الطواف

زاوية مسار الطواف هي الزاوية بين متجه سرعة الجرم المداري (= المتجه المماس لمسار المدار الفوري) والمستوى الأفقي المحلي. في ظل الافتراض القياسي لحفظ الزخم الزاوي $\phi$ ، فإن زاوية مسار الطيران:^[6]

h\,=r\,v\,\cos \phi

حيث:

$h\,$ هو الزخم الزاوي النسبي النوعي للمدار،
$v\,$ هو السرعة المدارية للجرم المداري،
$r\,$ هو المسافة الشعاعية للجسم المداري من الجسم المركزي،
$\phi \,$ هو زاوية مسار الطواف.

$\psi$ هي الزاوية بين متجه السرعة المدارية والمحور شبه الرئيسي. $\nu$ هو الانحراف المحلي الحقيقي. $\phi =\nu +{\frac {\pi }{2}}-\psi$ ، لذلك،

\cos \phi =\sin(\psi -\nu )=\sin \psi \cos \nu -\cos \psi \sin \nu ={\frac {1+e\cos \nu }{\sqrt {1+e^{2}+2e\cos \nu }}}

\tan \phi ={\frac {e\sin \nu }{1+e\cos \nu }}

حيث $e$ هو الانحراف المركزي.

يرتبط الزخم الزاوي بحاصل الضرب المتجهي لموقع الجسم وسرعته، والذي يتناسب مع جيب الزاوية بين هذين المتجهين. هنا يتم تعريف $\phi$ على أنه الزاوية التي تختلف عن ذلك بزاوية 90 درجة، لذلك يظهر جيب التمام في مكان الجيب.

معادلة الحركة

مقال رئيسي: معادلة المدار

من الموضع والسرعة الأولية

تحدد معادلة المدار مسار جرم مدار $m_{2}\,\!$ حول الجرم المركزي $m_{1}\,\!$ بالنسبة لـ $m_{1}\,\!$ ، بدون تحديد الموقع كدالة للزمن. إذا كان الانحراف أقل من 1، فإن معادلة الحركة تصف مدار إهليلجي. نظراً لأن معادلة كبلر $M=E-e\sin E$ ليس لها حل مغلق الشكل للانحراف الامركزي (E) من حيث متوسط الانحراف (M)، فإن معادلات الحركة كدالة متوسط الزمن لها أيضاً الحلول العددية المتوفرة لكليهما.

ومع ذلك، يمكن تحديد معادلات مدار زمنية مستقلة في صيغة مغلقة من مدار إهليلجي بالنسبة إلى جسم مركزي من مجرد موضع أولي ( $\mathbf {r}$ ) والسرعة ( $\mathbf {v}$ ).

في هذه الحالة، من الملائم استخدام الافتراضات التالية التي تختلف بعض الشيء عن الافتراضات القياسية المذكورة أعلاه:

يقع مركز الجرم المركزي عند الأصل وهو التركيز الرئيسي ( $\mathbf {F1}$ ) للقطع الناقص (يمكن أيضاً استخدام مركز الكتلة بدلاً من ذلك إذا كان الجرم المداري له كتلة كبيرة).
كتلة الجرم المركزي (m1) معروفة.
يُعرف موضع الجرم المداري الأولي ( $\mathbf {r}$ ) وسرعته ( $\mathbf {v}$ ).
يقع القطع الناقص في مستوى XY.

يمكن إجراء الافتراض الرابع دون فقدان العمومية لأن أي ثلاث نقاط (أو ناقلات) يجب أن تقع داخل مستوى مشترك. في ظل هذه الافتراضات، يجب أن يقع التركيز الثاني (يسمى أحياناً التركيز "الفارغ") ضمن المستوى XY: $\mathbf {F2} =\left(f_{x},f_{y}\right)$ .

استخدام المتجهات

المعادلة العامة للقطع الناقص بحكم هذه الافتراضات باستخدام المتجهات هي:

|\mathbf {F2} -\mathbf {p} |+|\mathbf {p} |=2a\qquad \mid z=0

حيث:

$a\,\!$ هو طول نصف المحور الرئيسي.
$\mathbf {F2} =\left(f_{x},f_{y}\right)$ هو التركيز الثاني ("الفارغ").
$\mathbf {p} =\left(x,y\right)$ هي أي قيمة (x,y) تحقق المعادلة.

يمكن حساب طول نصف المحور الرئيسي (a) على النحو التالي:

a={\frac {\mu |\mathbf {r} |}{2\mu -|\mathbf {r} |\mathbf {v} ^{2}}}

where $\mu \ =Gm_{1}$ وهو بارامتر الجاذبية القياسية.

يمكن إيجاد التركيز الفارغ ( $\mathbf {F2} =\left(f_{x},f_{y}\right)$ ) أولاً بتحديد متجه الانحراف:

\mathbf {e} ={\frac {\mathbf {r} }{|\mathbf {r} |}}-{\frac {\mathbf {v} \times \mathbf {h} }{\mu }}

حيث أن $\mathbf {h}$ هو الزخم الزاوي المحدد للجرم المداري:^[7]

\mathbf {h} =\mathbf {r} \times \mathbf {v}

إذاً

\mathbf {F2} =-2a\mathbf {e}

استخدام إحداثيات XY

يمكن القيام بذلك باستخدام الإحداثيات الديكارتية باستخدام الإجراء التالي:

المعادلة العامة للقطع الناقص تحت الافتراضات المذكورة أعلاه هي:

{\sqrt {\left(f_{x}-x\right)^{2}+\left(f_{y}-y\right)^{2}}}+{\sqrt {x^{2}+y^{2}}}=2a\qquad \mid z=0

يعطى:

r_{x},r_{y}\quad

إحداثيات الموضع الأولي

v_{x},v_{y}\quad

إحداثيات السرعة الأولية

و

\mu =Gm_{1}\quad

ثابت الجاذبية

إذاً:

h=r_{x}v_{y}-r_{y}v_{x}\quad

الزخم الزاوي النوعي

r={\sqrt {r_{x}^{2}+r_{y}^{2}}}\quad

المسافة الأولية من F1 (في الأصل):

a={\frac {\mu r}{2\mu -r\left(v_{x}^{2}+v_{y}^{2}\right)}}\quad

طول نصف المحور الرئيسي

e_{x}={\frac {r_{x}}{r}}-{\frac {hv_{y}}{\mu }}\quad

إحداثيات متجه الانحراف المداري:

e_{y}={\frac {r_{y}}{r}}+{\frac {hv_{x}}{\mu }}\quad

أخيراً، إحداثيات التركيز الفارغة

f_{x}=-2ae_{x}\quad

f_{y}=-2ae_{y}\quad

الآن يمكن تطبيق قيم fx، fy وa الناتجة على معادلة القطع الناقص العامة أعلاه.

البارامترات المدارية

حالة الجرم المداري في أي وقت محدد تُعرَّف بموقع الجرم المداري وسرعته بالنسبة إلى الجرم المركزي، والتي يمكن تمثيلها بالإحداثيات الديكارتية ثلاثية الأبعاد (موضع الجرم المداري ممثلاً بـ x وy وz) ومكونات ديكارتية مماثلة لسرعة الجسم المداري. يُطلق على هذه المجموعة المكونة من ست متغيرات، بالإضافة إلى الزمن، متجهات حالة المدار. نظراً لمجموعة الجرمين، فإنهما يحددان المدار الكامل. الحالات الأكثر عمومية مع هذه الدرجة الستة من الحرية هي المدار الإهليلجي والمدار القطع المكابلي. الحالات الخاصة مع عدد أقل من درجات الحرية هي المدار الدائري والمدار المكافيء.

لأن ستة متغيرات على الأقل مطلوبة تماماً لتمثيل مدار بيضاوي تماماً مع هذه المجموعة من البارامترات، فإن ستة متغيرات مطلوبة لتمثيل مدار بأي مجموعة من البارامترات. مجموعة أخرى من ستة بارامترات شائعة الاستخدام هي عناصر مدارية.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

النظام الشمسي

في النظام الشمسي، تدور الكواكب والكويكبات ومعظم المذنبات وبعض قطع المخلفات الفضائية تقريباً في مدارات إهليلجية حول الشمس.

بالمعنى الحرفي، يدور كلا الجرمين حول نفس بؤرة مدار إهليلجي، الذي يكون أقرب إلى الجرم الأكثر كتلة، ولكن عندما يكون أحد الجرمين أكثر كتلة بشكل كبير، مثل الشمس بالنسبة للأرض، فقد يتم احتواء البؤرة داخل الجرم الأكبر كتلة، وبالتالي يقال أن الأصغر يدور حوله.

يوضح المخطط التالي لنقطة الحضيض ونقطة الأوج للكواكب والكواكب القزمية والمذنب هالي تباين انحراف مداراتها الإهليلجية. بالنسبة لمثل هذه المسافات من الشمس، تشير القضبان الأوسع إلى انحراف أكبر. لاحظ شبه الصفر من انحراف الأرض والزهرة مقارنة بالانحراف الهائل لمذنب هالي وإيريس.

يوضح الرسم البياني مسافات الأجسام المختارة للنظام الشمسي من الشمس. تتوافق الحواف اليسرى واليمنى لكل شريط مع الحضيض والأوج للجسم، على التوالي، وبالتالي فإن القضبان الطويلة تشير إلى انحراف مداري كبير. يبلغ قطر الشمس 0.7 مليون كيلومتر، ويبلغ قطر المشتري (أكبر كوكب) 0.07 مليون كيلومتر، وكلاهما صغير جداً بحيث لا يمكن حلهما في هذه الصورة.

مدار إهليلجي شعاعي

يمكن أن يكون المسار الشعاعي عبارة عن مقطع خط مزدوج، وهو بيضاوي (إهليلجي) مشوه مع نصف المحور الصغير = 0 وانحراف = 1. على الرغم من أن الانحراف هو 1، إلا أنه ليس مداراً مكافئاً. تنطبق معظم خواص وصيغ المدارات الإهليلجية. ومع ذلك، لا يمكن إغلاق المدار. إنه مدار مفتوح يتوافق مع الجزء من القطع الناقص المشوه من اللحظة التي تلمس فيها الأجسام بعضها البعض وتتحرك بعيداً عن بعضها البعض حتى تلمس بعضها البعض مرة أخرى. في حالة كتل النقطة، يمكن إجراء مدار كامل واحد، بدءاً من نقطة الانطلاق وينتهي بنقطة تفرد. تكون السرعات في البداية والنهاية لانهائية في اتجاهين متعاكسين وتكون الطاقة الكامنة مساوياً لـ ناقص اللانهاية.

مدار إهليلجي شعاعي هو حل لمسألة جسمين في وقت ما بسرعة صفرية، كما في حالة إسقاط جسم (بغض النظر عن مقاومة الهواء).

التاريخ

كان [[البابليون أول من أدرك أن حركة الشمس على طول مسار الشمس لم تكن موحدة، على الرغم من أنهم لم يكونوا على علم بسبب ذلك؛ من المعروف اليوم أن هذا يرجع إلى أن الأرض تتحرك في مدار إهليلجي حول الشمس، مع تحرك الأرض بشكل أسرع عندما تكون أقرب إلى الشمس عند الحضيض والتحرك ببطء عندما تكون أبعد في الأوج.^[8]

في القرن السابع عشر، اكتشف يوهانس كيبلر أن المدارات التي تتحرك فيها الكواكب حول الشمس هي بيضاويات الشكل مع الشمس في أحد بؤرتيها، ووصف ذلك في قانونه الأول لحركة الكواكب. لاحقاً، أوضح إسحاق نيوتن ذلك باعتباره نتيجة لقانونه العام للجاذبية.

انظر أيضاً

المراجع

^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 11–12. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences: physics, chemistry, and habitability. New York, NY, USA: Cambridge University Press. pp. 29–31. ISBN 9781108411981.
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 33. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 27–28. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 15. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 18. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 17. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ David Leverington (2003), Babylon to Voyager and beyond: a history of planetary astronomy, Cambridge University Press, pp. 6–7, ISBN 0-521-80840-5

المصادر

D'Eliseo, Maurizio M. (2007). "The First-Order Orbital Equation". American Journal of Physics. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. doi:10.1119/1.2432126.
D'Eliseo, Maurizio M.; Mironov, Sergey V. (2009). "The Gravitational Ellipse". Journal of Mathematical Physics. 50 (2): 022901. arXiv:0802.2435. Bibcode:2009JMP....50a2901M. doi:10.1063/1.3078419.
Curtis, Howard D. (2019). Orbital Mechanics for Engineering Students (4th ed.). Butterworth-Heinemann. ISBN 978-0-08-102133-0.

وصلات خارجية

Java applet animating the orbit of a satellite in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
Apogee - Perigee Lunar photographic comparison
Aphelion - Perihelion Solar photographic comparison
http://www.castor2.ca

[1] Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 11–12. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[lissauer2019-2] Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences: physics, chemistry, and habitability. New York, NY, USA: Cambridge University Press. pp. 29–31. ISBN 9781108411981.

[3] Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 33. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[4] Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 27–28. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[5] Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 15. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[6] Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 18. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[7] Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 17. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[8] David Leverington (2003), Babylon to Voyager and beyond: a history of planetary astronomy, Cambridge University Press, pp. 6–7, ISBN 0-521-80840-5

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]