سقوط حر

سقوط حر لتفاحة

في الفيزياء النيوتنية، السقوط الحر هو أي حركة للجسم حيث أن الجاذبية هي القوة الوحيدة التي تؤثر عليه. في حالة نظرية النسبية العامة، حيث يتم اختصار الجاذبية إلى انحناء الزمكان، لا يخضع الجسم في حالة السقوط الحر لأي قوة مؤثرة عليه.

في المفهوم الفني لمصطلح "السقوط الحر"، فإن الجسم لا يتعرض للسقوط بالمعنى التقليدي للمصطلح. ويمكن أن يكون جسماً يتحرك باتجاه الأعلى لا يعتبر عادة كجسم ساقط، ولكن إذا كان يتعرض لقوة الجاذبية فقط، فيقال إنه في حالة سقوط حر. وبالتالي، يتعرض القمر للسقوط الحر حول الأرض، على الرغم من أن سرعته المدارية تبقيه في مدار بعيد جداً عن سطح الأرض.

في حقل جاذبية متجانس تقريباً، تعمل الجاذبية على كل جزء من الجسم بشكل تقريبي بالتساوي. عند عدم وجود قوى أخرى، مثل القوة العمودية المبذولة بين الجسم (على سبيل المثال، رائد فضاء في المدار) والأجسام المحيطة به، فإن ذلك يؤدي إلى شعور بانعدام الوزن، وهو حالة تحدث أيضاً عندما يكون حقل الجاذبية ضعيفاً (مثل الحالة التي يكون فيها بعيداً عن أي مصدر للجاذبية).

غالباً ما يُستخدم مصطلح "السقوط الحر" بمعنى أشمل من المفهوم الدقيق المعرف أعلاه. وبالتالي، يشار أيضاً إلى السقوط عبر الغلاف الجوي بدون استخدام پاراشوت أو جهاز رفع كسقوط حر. تمنع القوى الهوائية في مثل هذه الحالات الوصول إلى حالة عدم الوزن الكاملة، وبالتالي ينتج عن السقوط الحر للمظليين بعد الوصول إلى السرعة الحدية شعور بدعم وزن الجسم على وسادة من الهواء.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

التاريخ

في العالم الغربي قبل القرن السادس عشر، كان من المفترض عموماً أن سرعة جسم ساقط تكون متناسبة مع وزنه - وهذا يعني أنه كان من المتوقع أن يسقط جسم يزن 10 كجم بمعدل 10 مرات أسرع من جسم مماثل بوزن 1 كجم عبر نفس الوسط. ناقش الفيلسوف اليوناني القديم أرسطو (384-322 ق.م.) الأجسام الساقطة في كتابه "الفيزياء" (الجزء السابع)، وهو واحد من أقدم الكتب في الميكانيكا (انظر الفيزياء الأرسطية). على الرغم من ذلك، في القرن السادس، تحدى يوحنا النحوي هذا البرهان وقال أن كرتين بأوزان مختلفة جداً ستسقطان بسرعة تقريباً متساوية بناءً على الملاحظة.^[1]

في العراق في القرن الثاني عشر ، قدم ابن ملكا البغدادي شرحاً لتسارع الجاذبية للأجسام المتساقطة. ووفقاً لشلومو پينز، فإن نظرية البغدادي للحركة كانت "أقدم نفي لقانون أرسطو الديناميكي الأساسي [أي أن القوة الثابتة تنتج حركة موحدة]، وبالتالي فهي توقعاً بطريقة غامضة للقانون الأساسي للميكانيكا الكلاسيكية [أي أن القوة المطبقة باستمرار تنتج تسارعاً]. "[2]"^[2]

وفقاً لقصة قد تكون مزيفة، في 1589-1592 أسقط گاليليو جسمين غير متساويين من الكتلة من برج پيزا المائل. ونظراً إلى السرعة التي سيحدث بها مثل هذا السقوط، فمن المشكوك فيه أن يكون گاليليو قد استخرج الكثير من المعلومات من هذه التجربة. معظم ملاحظاته عن الأجسام المتساقطة كانت في الحقيقة لجثث تتدحرج على منحدرات. أدى هذا إلى إبطاء الأمور بدرجة كافية لدرجة أنه تمكن من قياس الفترات الزمنية باستخدام ساعة مائية ونبضه (لم يتم اختراع ساعات التوقيف حتى ذلك الحين). وقام بتكرار هذا "مئة مرة كاملة" حتى حقق "دقة تصل إلى أن الانحراف بين ملاحظتين عُشر نبضة". في 1589-1592، كتب جاليليو De Motu Antiquiora، وهي مخطوطة غير منشورة عن حركة الأجسام الساقطة.^{[بحاجة لمصدر]}

أمثلة

تشمل أمثلة على الأجسام المتساقطة حراً:

مركبة فضائية (في الفضاء) بدون دفع (مثل التحليق المستمر، أو المسار الفلكي الفاصل (علم القذائف) الذي يرتفع لبضع دقائق ثم ينحدر).
جسم مُسقط من أعلى أنبوب إسقاط.
جسم ملقى لأعلى أو شخص يقفز من الأرض بسرعة منخفضة (أي طالما أن المقاومة الهوائية لا تُعَدُّ ملحوظة مقارنة بالوزن).

تقنياً، يكون الجسم في حالة سقوط حر حتى عندما يتحرك باتجاه الأعلى أو يكون ساكناً تماماً لفترة قصيرة عند القمة من حركته. إذا كانت الجاذبية هي القوة الوحيدة المؤثرة، فإن التسارع^[3] دائماً إلى الأسفل وله نفس المقدار لجميع الأجسام، والتي عادة ما يُرمز له بـ $g$ .

نظراً لأن جميع الأشياء تسقط بالمعدل نفسه في غياب أي قوة أخرى، فإن الأشياء والأشخاص سيختبرون انعدام الوزن في هذه المواقف.

بعض الأمثلة على الأشياء التي لا تكون في حالة سقوط حر:

التحليق في الطائرة: هناك أيضاً قوة إضافية تسمى الرفع.
الوقوف على الأرض: تعادل القوة الجاذبية بقوة عكسية تسمى "القوة العمودية" من الأرض.
النزول إلى الأرض باستخدام الپاراشوت، التي تعادل قوة الجاذبية بقوة السحب الديناميكية (وببعض الپاراشوتات، تُضاف قوة رفع إضافية).

لا يعتبر مثال القافز المظلي الساقط الذي لم ينشر المظلة بعد سقوطاً حراً من منظور فيزيائي، نظراً لأنه يعاني من قوة السحب التي تساوي وزنه بمجرد بلوغه السرعة الحدية (انظر أدناه).

زمن السقوط المقاس لكرة فولاذية صغيرة تسقط من ارتفاعات مختلفة. تتوافق البيانات جيداً مع زمن السقوط المتوقع لـ

{\sqrt {2h/g}}

، حيث h هو الارتفاع وg هو تسارع السقوط الحر بسبب الجاذبية.

بالقرب من سطح الأرض، سيتسارع جسم في حالة سقوط حر في فراغ بسرعة 9.8 m/s²، بغض النظر عن كتلته. مع مقاومة الهواء التي تعمل على جسم تم إسقاطه، سيصل الجسم في النهاية إلى السرعة النهائية، والتي تبلغ حوالي 53 m/s (190 km/h or 118 mph؛^[4]) لقافز مظلي بشري. تعتمد السرعة النهائية على العديد من العوامل بما في ذلك الكتلة، معامل السحب، ومساحة السطح النسبية ولن تتحقق إلا إذا كان السقوط من ارتفاع كافٍ. سيصل لاعب القفز المظلي النموذجي في وضع النسر المنتشر إلى السرعة النهائية بعد حوالي 12 ثانية، وخلال هذه الفترة سيكونون قد سقطوا حوالي 450 متر (1500 قدم).^[4]

أُظهر السقوط الحر على القمر بواسطة رائد الفضاء ديڤد سكوت في 2 أغسطس 1971. أطلق في نفس الوقت مطرقة وريشة من نفس الارتفاع فوق سطح القمر. سقطت المطرقة والريشة بنفس المعدل وضربت السطح في نفس الوقت. أظهر هذا اكتشاف گاليليو أنه في حالة عدم وجود مقاومة للهواء، فإن كل الأجسام تتعرض لنفس التسارع بسبب الجاذبية. ومع ذلك يبلغ تسارع الجاذبية على سطح القمر حوالي 1.63 m/s²، أو حوالي ¹⁄₆ على سطح الأرض.

السقوط الحر في ميكانيكا نيوتن

حقل جاذبية منتظم بدون مقاومة الهواء

وهي الحالة "النموذجية" للحركة العمودية لجسم يتساقط على مسافة صغيرة قريبة من سطح كوكب. إنه تقريب جيد في الهواء طالما أن قوة الجاذبية على الجسم أكبر بكثير من قوة مقاومة الهواء، أو بالمقابل تكون سرعة الجسم دائماً أقل بكثير من السرعة الحرجة (انظر أدناه).

v(t)=v_{0}-gt\,

y(t)=v_{0}t+y_{0}-{\frac {1}{2}}gt^{2}

حيث

v_{0}\,

هي السرعة الابتدائية (m/s).

v(t)\,

هي السرعة العمودية بالنسبة للزمن (m/s).

y_{0}\,

هي الارتفاع الأولي (m).

y(t)\,

الارتفاع تابع للزمن (m).

t\,

الوقت المار (s).

g\,

هو التسارع بسبب الجاذبية(9.81 m/s² بالقرب من سطح الأرض).

إذا كانت السرعة الابتدائية تساوي صفر، فإن المسافة الساقطة من الموضع الأولي ستزداد بمربع الوقت المنقضي. علاوة على ذلك، نظراً لأن مجموع الأرقام الفردية للمربعات الكاملة، فإن المسافة الساقطة في الفترات الزمنية المتتالية تتزايد كأرقام فردية. هذا الوصف لسلوك الأجسام الساقطة قدمه گاليليو سابقاً.^[5]

حقل جاذبية منتظم مع مقاومة الهواء

تسارع نيزك صغير عند دخوله جو الأرض بسرعات أولية مختلفة

هذه الحالة، التي تنطبق على القفز بالمظلات أو المظليين أو أي جسم ذي كتلة، $m$ ،ومساحة عرضية $A$ ، مع رقم رينولدز أعلى بكثير من رقم رينولدز الحدي، بحيث تتناسب مقاومة الهواء مع مربع سرعة السقوط ، $v$ ، بمعادلة الحركة

m{\frac {\mathrm {d} v}{\mathrm {d} t}}=mg-{\frac {1}{2}}\rho C_{\mathrm {D} }Av^{2}\,,

حيث $\rho$ هي كثافة الهواء و $C_{\mathrm {D} }$ هو معامل السحب، يُفترض أنه ثابت على الرغم من أنه بشكل عام سيعتمد على رقم رينولدز. بافتراض سقوط جسم من السكون وعدم حدوث تغيير في كثافة الهواء مع الارتفاع، فإن الحل هو:

v(t)=v\tanh \left({\frac {gt}{v}}\right),

حيث يتم إعطاء السرعة الحدية بواسطة

v_{\infty }={\sqrt {\frac {2mg}{\rho C_{D}A}}}\,.

يمكن دمج سرعة الجسم مقابل الزمن بمرور الزمن للعثور على الوضع العمودي كدالة للزمن:

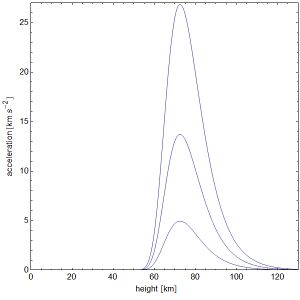
y=y_{0}-{\frac {v_{\infty }^{2}}{g}}\ln \cosh \left({\frac {gt}{v_{\infty }}}\right).

باستخدام الرقم 56 m/s للسرعة الحدية للإنسان، يتبين أنه بعد 10 ثوانٍ سيكون قد هبط 348 متراً وبلغ 94٪ من السرعة النهائية، وبعد 12 ثانية سيكون قد سقط 455 متراً وسيصاب بلغت 97٪ من السرعة النهائية. ومع ذلك، عندما لا يمكن افتراض أن كثافة الهواء ثابتة، كما هو الحال بالنسبة للأجسام التي تسقط من ارتفاع عالٍ، يصبح حل معادلة الحركة أكثر صعوبة في الحل تحليلياً وعادة ما تكون المحاكاة العددية للحركة ضرورية. يوضح الشكل القوى المؤثرة على النيازك المتساقطة عبر الغلاف الجوي العلوي للأرض. تنتمي قفزة HALO، بما في ذلك قفزات جوزف كتنگر وفيلكس بومگارتنر، أيضاً إلى هذه الفئة.^[6]

قانون الجاذبية المعكوس تربيعياً لحقل الجاذبية

يمكن القول أن جسمين في الفضاء يدوران حول بعضهما البعض في حالة عدم وجود قوى أخرى في حالة سقوط حر حول بعضهما البعض، على سبيل المثال أن القمر أو ساتل "الساقط" حول الأرض، أو أن كوكباً "يسقط" حول الشمس. يعني افتراض الأجسام الكروية أن معادلة الحركة تحكمها قانون الجذب العام لنيوتن، مع حلول مسألة الجاذبية ثنائية الجسم كونها مدارات إهليلجية تخضع قوانين كپلر للحركة الكوكبية. ويمكن توضيح العلاقة بين الأجسام الساقطة بالقرب من الأرض والأجسام التي تدور في مدارات بشكل أفضل من خلال التجربة النظرية، مقذوف نيوتن.

يمكن اعتبار حركة جسمين يتحركان شعاعياً تجاه بعضهما البعض بدون زخم زاوي حالة خاصة لمدار إهليلجي من الانحراف المركزي e = 1 (مسار إهليلجي شعاعي). هذا يتيح حساب زمن السقوط الحر لأجسام نقطية على مسار شعاعي. يؤدي حل معادلة الحركة هذه إلى الحصول على الزمن كدالة للفصل بين الجسمين:

t(y)={\sqrt {\frac {{y_{0}}^{3}}{2\mu }}}\left({\sqrt {{\frac {y}{y_{0}}}\left(1-{\frac {y}{y_{0}}}\right)}}+\arccos {\sqrt {\frac {y}{y_{0}}}}\right),

حيث

t

الزمن بعد بداية السقوط

y

المسافة بين مراكز الأجسام

y_{0}

القيمة الأولية لـ

y

\mu =G(m_{1}+m_{2})

پارامتر الجاذبية المعيارية.

بتعويض $y=0$ نحصل على زمن السقوط الحر.

يتم الحصول على الفصل كدالة للزمن من خلال معكوس المعادلة. يتم تمثيل المعكوس بالضبط بواسطة سلسلة القوة التحليلية:

y(t)=\sum _{n=1}^{\infty }\left[\lim _{r\to 0}\left({\frac {x^{n}}{n!}}{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} r^{\,n-1}}}\left[r^{n}\left({\frac {7}{2}}(\arcsin({\sqrt {r}})-{\sqrt {r-r^{2}}})\right)^{-{\frac {2}{3}}n}\right]\right)\right].

يعطي تقدير ذلك:^[7]^[8]

y(t)=y_{0}\left(x-{\frac {1}{5}}x^{2}-{\frac {3}{175}}x^{3}-{\frac {23}{7875}}x^{4}-{\frac {1894}{3031875}}x^{5}-{\frac {3293}{21896875}}x^{6}-{\frac {2418092}{62077640625}}x^{7}-\cdots \right)\ ,

حيث

$x=\left[{\frac {3}{2}}\left({\frac {\pi }{2}}-t{\sqrt {\frac {2\mu }{{y_{0}}^{3}}}}\right)\right]^{2/3}.$

السقوط الحر في نظرية النسبية العامة

في النسبية العامة، لا يخضع الجسم في السقوط الحر لأي قوة وهو جسم عطالي يتحرك على طول كروية الأرض. بعيدًا عن أي مصادر لانحناء الزمكان، حيث يكون الزمكان مسطحاً، تتفق نظرية نيوتن للسقوط الحر مع النسبية العامة. وإلا فإن الاثنين سيتعارضان. على سبيل المثال، يمكن للنسبية العامة تفسير حركة البداية للمدارات فقط، والاضمحلال المداري أو الدوامة للثنائيات المدمجة بسبب موجات الجاذبية، والنسبية في الاتجاه (التأثير الجيوديسي وتباطؤ الإطار المرجعي).

لاحظ گاليليو في تجاربه أن جميع الأجسام في السقوط الحر تتسارع بنفس المعدل، ثم جسدها في نظرية نيوتن كمساواة بين كتل الجاذبية والقصور الذاتي، وتأكد لاحقاً بالدقة العالية بواسطة الأشكال الحديثة من تجربة أوتڤوش، هو أساس مبدأ التكافؤ، الذي انطلقت منه نظرية النسبية العامة لأينشتاين في البداية.

انظر أيضاً

المراجع

^ Cohen, Morris R.; Drabkin, I. E., eds. (1958). A Source Book in Greek Science. Cambridge, MA: Harvard University Press. p. 220.
^ Pines, Shlomo (1970). "Abu'l-Barakāt al-Baghdādī , Hibat Allah". Dictionary of Scientific Biography. Vol. 1. New York: Charles Scribner's Sons. pp. 26–28. ISBN 0-684-10114-9.
(cf. Abel B. Franco (October 2003). "Avempace, Projectile Motion, and Impetus Theory", Journal of the History of Ideas 64 (4), p. 521-546 [528].)
^ "The Feynman Lectures on Physics Vol. I Ch. 8: Motion".
^ ^أ ^ب "Free fall graph" (PDF). Green Harbor Publications. 2010. Retrieved 14 March 2016.
^ Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2008-01-14). The Mechanical Universe: Introduction to Mechanics and Heat (in الإنجليزية). Cambridge University Press. p. 18. ISBN 978-0-521-71592-8.
^ An analysis of such jumps is given in Mohazzabi, P.; Shea, J. (1996). "High altitude free fall" (PDF). American Journal of Physics. 64 (10): 1242. Bibcode:1996AmJPh..64.1242M. doi:10.1119/1.18386.
^ Foong, S K (2008). "From Moon-fall to motions under inverse square laws". European Journal of Physics. 29 (5): 987–1003. Bibcode:2008EJPh...29..987F. doi:10.1088/0143-0807/29/5/012.
^ Mungan, Carl E. (2009). "Radial Motion of Two Mutually Attracting Particles" (PDF). The Physics Teacher. 47 (8): 502–507. Bibcode:2009PhTea..47..502M. doi:10.1119/1.3246467.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

وصلات خارجية

Freefall formula calculator
The Way Things Fall an educational website

[1] Cohen, Morris R.; Drabkin, I. E., eds. (1958). A Source Book in Greek Science. Cambridge, MA: Harvard University Press. p. 220.

[2] Pines, Shlomo (1970). "Abu'l-Barakāt al-Baghdādī , Hibat Allah". Dictionary of Scientific Biography. Vol. 1. New York: Charles Scribner's Sons. pp. 26–28. ISBN 0-684-10114-9.
(cf. Abel B. Franco (October 2003). "Avempace, Projectile Motion, and Impetus Theory", Journal of the History of Ideas 64 (4), p. 521-546 [528].)

[3] "The Feynman Lectures on Physics Vol. I Ch. 8: Motion".

[Greenharbor-4] أ ^ب "Free fall graph" (PDF). Green Harbor Publications. 2010. Retrieved 14 March 2016.

[5] Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2008-01-14). The Mechanical Universe: Introduction to Mechanics and Heat (in الإنجليزية). Cambridge University Press. p. 18. ISBN 978-0-521-71592-8.

[6] An analysis of such jumps is given in Mohazzabi, P.; Shea, J. (1996). "High altitude free fall" (PDF). American Journal of Physics. 64 (10): 1242. Bibcode:1996AmJPh..64.1242M. doi:10.1119/1.18386.

[7] Foong, S K (2008). "From Moon-fall to motions under inverse square laws". European Journal of Physics. 29 (5): 987–1003. Bibcode:2008EJPh...29..987F. doi:10.1088/0143-0807/29/5/012.

[8] Mungan, Carl E. (2009). "Radial Motion of Two Mutually Attracting Particles" (PDF). The Physics Teacher. 47 (8): 502–507. Bibcode:2009PhTea..47..502M. doi:10.1119/1.3246467.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]