جداء نقطي

"Scalar product" redirects here. For the abstract scalar product, see Inner product space. For the product of a vector and a scalar, see Scalar multiplication.

في الرياضيات، الجداء النقطي dot product أو الجداء العددي scalar product هي عملية جبرية تأخذ تسلسلين متساويي الطول من الأرقام (عادةً شعاع إحداثي، وتعيد رقماً واحداً. في الهندسة الإقليدية، يتم استخدام المنتج النقطي لـ الإحداثيات الديكارتية لاثنين من الأشعة على نطاق واسع. غالباً ما يطلق عليه الجداء الداخلي (أو نادراً الجداء الإسقاطي) من الفضاء الإقليدي، على الرغم من أنه ليس الجداء الداخلي الوحيد الذي يمكن تحديده في الفضاء الإقليدي (راجع فضاء الجداء الداخلي للمزيد).

جبرياً، الجداء النقطي هو مجموع النواتج من الإدخالات المقابلة لتسلسل الأرقام. هندسياً، هو ناتج المطال الإقليدي للشعاعين و جيب التمام للزاوية بينهما. هذه التعريفات متكافئة عند استخدام الإحداثيات الديكارتية. في الهندسة الحديثة، يتم تعريف الفضاء الإقليدي غالباً باستخدام فضاء الشعاع. في هذه الحالة، يتم استخدام الجداء النقطي لتعريف الأطوال (طول الشعاع هو الجذر التربيعي للجداء النقطي للشعاع بحد ذاته) والزوايا (جيب تمام زاوية الشعاعين هو حاصل القسمة للجداء النقطي بحاصل ضرب أطوالهم).

اسم "المنتج النقطي" مشتق من نقطة مركزية " · "، التي غالباً ما تستخدم لتعيين هذه العملية; يؤكد الاسم البديل "الجداء العددي" على أن النتيجة هي عددية، وليس شعاعية، كما هو الحال بالنسبة للجداء الشعاعي في فضاء ثلاثي الأبعاد.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تعريف

يمكن تعريف الجداء النقطي جبرياً أو هندسياً. يعتمد التعريف الهندسي على مفاهيم الزاوية والمسافة (حجم الأشعة). تكافؤ هذين التعريفين يعتمد على وجود نظام إحداثيات ديكارتي للفضاء الإقليدي.

في التقديمات الحديثة لـ الهندسة الإقليدية، يتم تحديد نقاط الفضاء من حيث الإحداثيات الديكارتية، و الفضاء الإقليدي نفسه يتم تحديده بشكل شائع مع فضاء إحداثي حقيقي Rⁿ. في مثل هذا الشرح، يتم تحديد مفاهيم الطول والزوايا عن طريق الجداء العددي. ويتم تعريف طول الشعاع على أنه الجذر التربيعي للجداء النقطي للشعاع في حد ذاته، و جيب التمام للزاوية (غير الموجهة) لشعاعين بطول واحد يتم تعريفه كجداء نقطي. لذا فإن تكافؤ التعريفين للجداء النقطي هو جزء من تكافؤ الصيغتين الكلاسيكية والحديثة للهندسة الإقليدية.

 التعريف الجبري

يُعرَّف الجداء النقطي لشعاعين a = [a₁, a₂, …, a_n] and b = [b₁, b₂, …, b_n]  :

$\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} =\sum _{i=1}^{n}{\color {red}a}_{i}{\color {blue}b}_{i}={\color {red}a}_{1}{\color {blue}b}_{1}+{\color {red}a}_{2}{\color {blue}b}_{2}+\cdots +{\color {red}a}_{n}{\color {blue}b}_{n}$

حيث تشير Σ إلى الجمع و n هي البعد من فضاء الشعاع. على سبيل المثال، في فضاء ثلاثي الأبعاد، يكون الجداء النقطي للأشعة [1, 3, −5] و [4, −2, −1]:

${\begin{aligned}\ [{\color {red}1,3,-5}]\cdot [{\color {blue}4,-2,-1}]&=({\color {red}1}\times {\color {blue}4})+({\color {red}3}\times {\color {blue}-2})+({\color {red}-5}\times {\color {blue}-1})\\&=4-6+5\\&=3\end{aligned}}$

إذا تم تحديد الأشعة باستخدام مصفوفات نسقية، يمكن أيضاً كتابة الجداء النقطي كـ جداء مصفوفة

$\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} =\mathbf {\color {red}a} \mathbf {\color {blue}b} ^{\mathsf {T}},$

حيث $\mathbf {\color {blue}b} ^{\mathsf {T}}$ يدل على منقول $\mathbf {\color {blue}b}$.

للتعبير عن المثال أعلاه بهذه الطريقة، يتم ضرب مصفوفة 1 × 3 (شعاع نسقي) في مصفوفة 3 × 1 (شعاع عمودي) للحصول على مصفوفة 1 × 1 التي تم تحديدها بمدخلها الفريد:

${\begin{bmatrix}\color {red}1&\color {red}3&\color {red}-5\end{bmatrix}}{\begin{bmatrix}\color {blue}4\\\color {blue}-2\\\color {blue}-1\end{bmatrix}}=\color {purple}3$.

 التعريف الهندسي

رسم توضيحي يوضح كيفية إيجاد الزاوية بين الشعاعين باستخدام الجداء النقطي

حساب الزوايا المترابطة المتناظرة الهندسة الجزيئية رباعية السطوح باستخدام جداء نقطي

في الفضاء الإقليدي، الشعاع الإقليدي هو شيء هندسي يمتلك مقداراً واتجاهاً. يمكن تصوير الشعاع كسهم. حجمه هو طوله، واتجاهه هو الاتجاه الذي يشير إليه السهم. يُشار إلى حجم الشعاع a بواسطة $\left\|\mathbf {a} \right\|$. الجداء النقطي لشعاعين إقليديين a و b "يتم تعريفه بواسطة

$\mathbf {a} \cdot \mathbf {b} =\|\mathbf {a} \|\ \|\mathbf {b} \|\cos \theta ,$

حيث θ هي الزاوية بين a و b.

على وجه الخصوص، إذا كانت المتجهات a و b متعامدة (أي أن زاويتها هي π / 2 أو 90 درجة)، إذاً $\cos {\frac {\pi }{2}}=0$، مما يعني أن

$\mathbf {a} \cdot \mathbf {b} =0.$

في الطرف الآخر، إذا كانت ذات اتجاه مشترك، فإن الزاوية بينهما تساوي صفراً:$\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|$ هذا يعني أن الجداء النقطي للشعاع a مع نفسه هو

$\mathbf {a} \cdot \mathbf {a} =\left\|\mathbf {a} \right\|^{2},$

والذي يعطي

$\left\|\mathbf {a} \right\|={\sqrt {\mathbf {a} \cdot \mathbf {a} }},$

وهي صيغة الطول الإقليدي للشعاع.

 الإسقاط العددي والخصائص الأولية

الإسقاط العددي

يُعطى الإسقاط العددي (أو المكون العددي) لشعاع إقليدي a في اتجاه الشعاع الإقليدي b:$a_{b}=\left\|\mathbf {a} \right\|\cos \theta ,$ حيث تكون θ الزاوية بين a و b.

من حيث التعريف الهندسي للجداء النقطي، يمكن إعادة كتابة هذا

$a_{b}=\mathbf {a} \cdot {\widehat {\mathbf {b} }},$

حيث ${\widehat {\mathbf {b} }}=\mathbf {b} /\left\|\mathbf {b} \right\|$ هو شعاع الوحدة في اتجاه b.

قانون التوزيع للخداء النقطي

وهكذا يتم تمييز الجداء النقطي هندسياً بواسطة

$\mathbf {a} \cdot \mathbf {b} =a_{b}\left\|\mathbf {b} \right\|=b_{a}\left\|\mathbf {a} \right\|.$

يكون الجداء النقطي، المعرّف بهذه الطريقة، متجانس تحت القياس في كل متغير، مما يعني أنه لأي عدد قياسي α،

$(\alpha \mathbf {a} )\cdot \mathbf {b} =\alpha (\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot (\alpha \mathbf {b} ).$

كما أنه يستوفي قانون التوزيع، بمعنى ذلك

$\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

يمكن تلخيص هذه الخصائص بالقول إن الجداء النقطي هو صيغة ثنائية الخطية. علاوة على ذلك، فإن هذا الشكل الثنائي الخطي هو تحديد إيجابي، مما يعني أن $\mathbf {a} \cdot \mathbf {a}$ ليست سالبة أبداً، وتكون صفراً إذا وفقط إذا $\mathbf {a} =\mathbf {0}$—الشعاع الصفري.

وبالتالي، فإن الجداء النقطي يعادل ضرب معيار (طول) b بمعيار إسقاط a على b.

 معادلة التعاريف

إذا كان e₁, ..., e_n هي أشعة الأساس القياسي في Rⁿ، إذاً قد نكتب

${\begin{aligned}\mathbf {a} &=[a_{1},\dots ,a_{n}]=\sum _{i}a_{i}\mathbf {e} _{i}\\\mathbf {b} &=[b_{1},\dots ,b_{n}]=\sum _{i}b_{i}\mathbf {e} _{i}.\end{aligned}}$

الأشعة e_i هي أساس متعامد ، مما يعني أن لها طول وحدة وزوايا قائمة مع بعضها البعض. ومن ثم لأن هذه الأشعة لها وحدة طول

$\mathbf {e} _{i}\cdot \mathbf {e} _{i}=1$

وبما أنهم يشكلون زوايا قائمة مع بعضهم البعض، إذا i ≠ j,

$\mathbf {e} _{i}\cdot \mathbf {e} _{j}=0.$

لذلك بشكل عام يمكننا القول:

$\mathbf {e} _{i}\cdot \mathbf {e} _{j}=\delta _{ij}.$

حيث تكون δ _ij دلتا كرونيكر.

مكونات الشعاع في أساس متعامد

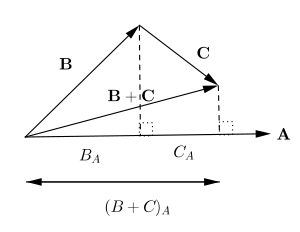
أيضاً، من خلال التعريف الهندسي، لأي شعاع e_i والشعاع a، نلاحظ

$\mathbf {a} \cdot \mathbf {e} _{i}=\left\|\mathbf {a} \right\|\,\left\|\mathbf {e} _{i}\right\|\cos \theta _{i}=\left\|\mathbf {a} \right\|\cos \theta _{i}=a_{i},$

حيث تكون a_i هو مكون الشعاع a في اتجاه e_i. يمكن رؤية الخطوة الأخيرة في المساواة من الشكل.

الآن تطبيق توزيعية النسخة الهندسية يعطيها الجداء النقطي

$\mathbf {a} \cdot \mathbf {b} =\mathbf {a} \cdot \sum _{i}b_{i}\mathbf {e} _{i}=\sum _{i}b_{i}(\mathbf {a} \cdot \mathbf {e} _{i})=\sum _{i}b_{i}a_{i}=\sum _{i}a_{i}b_{i},$

وهو بالضبط التعريف الجبري للجداء النقطي. إذن، الجداء النقطي الهندسي يساوي الجداء النقطي الجبري.

 الخصائص

يفي الجداء النقطي بالخصائص التالية إذا كانت a و b و c أشعة حقيقة و r عددي.

1. التبادلية:

   $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} ,$

   الذي يلي التعريف (θ هي الزاوية بين a و b):

   $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta =\left\|\mathbf {b} \right\|\left\|\mathbf {a} \right\|\cos \theta =\mathbf {b} \cdot \mathbf {a} .$

2. التوزيعية على إضافة الشعاع:

   $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

3. ثنائية الخطية:

   $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

4. الضرب العددي:

   $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=c_{1}c_{2}(\mathbf {a} \cdot \mathbf {b} ).$

5. ليس ترابطية لأن الجداء النقطي بين (a ⋅ b) عددي والشعاع (c) لم يتم تعريفه، مما يعني أن التعبيرات المتضمنة في الخاصية الترابطية (a ⋅ b) ⋅ c أو a ⋅ (b ⋅ c) كلاهما غير محدد. نلاحظ مع ذلك أن خاصية الضرب العددية المذكورة سابقاً تسمى أحياناً "القانون الترابطي للجداء العددي والنقطي" أو يمكن للمرء أن يقول أن "الجداء النقطي ترابطي فيما يتعلق بالضرب العددي" لأن c (a ⋅ b) = (c a) ⋅ b = a ⋅ (c b).
6. التعامدية:

   شعاعين غير صفريين a وb هما متعامدان إذا وفقط إذا a ⋅ b = 0.

7. لا اختصارية:

   على عكس ضرب الأعداد العادية، حيث إذا ab = ac، فإن b تساوي دائماً c إلا إذا كانت a تساوي صفراً، فإن الجداء النقطي لا يخضع لقانون الاختصار:

   إذا a ⋅ b = a ⋅ c و a ≠ 0، إذا يمكننا أن نكتب: a ⋅ (b − c) = 0 بموجب قانون التوزيع؛ النتيجة أعلاه تقول أن هذا يعني فقط أن a عمودي على (b − c)، الذي لا يزال يسمح (b − c) ≠ 0، وبالتالي يسمح b ≠ c.

8. قاعدة الجداء:

   إذا كانت a و b (ذات قيمة شعاعية) دوال التفاضل، فإن المشتق (يدل عليه بعدد أولي ′) من a ⋅ b يعطى بالقاعدة (a ⋅ b)′ = a′ ⋅ b + a ⋅ b′.

 تطبيق لقانون جيب التمام

مثلث ذو حواف شعاعية a و b، مفصول بزاوية θ.

المقالة الرئيسية: Law of cosines

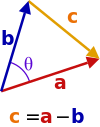
بالنظر إلى شعاعين a و b مفصول بزاوية θ (انظر الصورة على اليمين)، فإنهما يشكلان مثلثاً ضلع ثالث c = a − b. الجداء النقطي لذلك مع نفسه:

${\begin{aligned}\mathbf {\color {gold}c} \cdot \mathbf {\color {gold}c} &=(\mathbf {\color {red}a} -\mathbf {\color {blue}b} )\cdot (\mathbf {\color {red}a} -\mathbf {\color {blue}b} )\\&=\mathbf {\color {red}a} \cdot \mathbf {\color {red}a} -\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} -\mathbf {\color {blue}b} \cdot \mathbf {\color {red}a} +\mathbf {\color {blue}b} \cdot \mathbf {\color {blue}b} \\&={\color {red}a}^{2}-\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} -\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} +{\color {blue}b}^{2}\\&={\color {red}a}^{2}-2\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} +{\color {blue}b}^{2}\\{\color {gold}c}^{2}&={\color {red}a}^{2}+{\color {blue}b}^{2}-2{\color {red}a}{\color {blue}b}\cos {\color {purple}\theta }\\\end{aligned}}$

وهو قانون جيب التمام.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 جداء ثلاثي

المقالة الرئيسية: جداء ثلاثي

هناك نوعان من العمليات الثلاثية تتضمن الجداء النقطي و الجداء التقاطعي.

يتم تعريف الجداء الثلاثي العددي لثلاثة أشعة على أنه

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).$

قيمتها هي محدد المصفوفة التي تمثل أعمدتها الإحداثيات الديكارتية للأشعة الثلاثة. وهو الحجم المؤشَّر من متوازي سطوح محدد بالأشعة الثلاثة.

يتم تعريف جداء ثلاثي الأشعة بواسطة

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} ).$

هذه المطابقة، المعروفة أيضاً باسم صيغة لاگرانج، يمكن تذكرها باسم "BAC minus CAB"، مع مراعاة الأشعةالمنتشرة معاً. هذه الصيغة لها تطبيقات في تبسيط حسابات الأشعة في الفيزياء.

 الفيزياء

في الفيزياء، مطال الشعاع هو العددية بالمعنى المادي (أي الكمية المادية مستقلة عن نظام الإحداثيات)، معبراً عنها بـ جداء قيمة عددية و وحدة مادية، وليس مجرد رقم. الجداء النقطي هو أيضاً عددي بهذا المعنى، معطى بواسطة الصيغة، مستقل عن نظام الإحداثيات. فمثً:

• العمل الميكانيكي هو الجداء النقطي لأشعة القوة و الإزاحة،
• القدرة هي الجداء النقطي لـ القوة و السرعة.

 التعميمات

 أشعة عقدية

بالنسبة إلى المتجهات التي تحتوي على مدخلات عقدية، فإن استخدام التعريف المعطى للجداء النقطي سيؤدي إلى خصائص مختلفة تماماً. على سبيل المثال، سيكون الجداء النقطي للمتجه بحد ذاته عدداً مركباً عشوائياً، ويمكن أن يكون صفراً دون أن يكون المتجه هو المتجه الصفري (تسمى هذه المتجهات متساوية الخواص)؛ وهذا بدوره سيكون له آثار على مفاهيم مثل الطول والزاوية. يمكن استعادة خصائص مثل معيار التحديد الإيجابي على حساب التخلي عن الخصائص المتماثلة والخطية للمنتج القياسي، من خلال التعريف البديل

$\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}},$

حيث b_i هو المرافق العقدي لـ b_i.يمكن أيضاً التعبير عنها بعبارات منقول مرافق (يُشار إليها بالحرف المرتفع H):

$\mathbf {a} \cdot \mathbf {b} =\mathbf {a} \mathbf {b} ^{H}.$

حيث يُفترض أن يتم تمثيل المتجهات كأشعة نسقية. ثم يكون الجداء العددي لأي متجه مع نفسه عدداً حقيقياً غير سالب، وهو غير صفري باستثناء المتجه الصفري. ومع ذلك، فإن هذا الجداء العددي هو خطي متماثل بدلاً من خطين: إنه خطي مترافق وليس خطي في a، والجداء القياسي غير متماثل، حيث

$\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}.$

الزاوية المحصورة بين متجهين مركبين تُعطى بواسطة

$\cos \theta ={\frac {\operatorname {Re} (\mathbf {a} \cdot \mathbf {b} )}{\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|}}.$

هذا النوع من الجداءات العددية مفيد، ويؤدي إلى مفهومين الشكل هيرميتي و فضاءات الجداء الداخلي العامة. الجداء الذاتي النقطي لمتجه معقد $\mathbf {a} \cdot \mathbf {a}$ هو تعميم لـ المربع المطلق لعدد مركب.

 الجداء الداخلي

المقالة الرئيسية: فضاء الجداء الداخلي

يعمم الجداء الداخلي الجداء النقطي على قضاءات متجه مجردة عبر مجال من العدديات، إما أن يكون مجال أعداد حقيقية$\mathbb {R}$أو مجال أعداد مركبة $\mathbb {C}$. عادة ما يتم الإشارة إليها باستخدام الأقواس الزاوية بواسطة $\left\langle \mathbf {a} \,,\mathbf {b} \right\rangle$.

الجداء الداخلي لمتجهين في مجال الأعداد المركبة هو، بشكل عام، عدد مركب، وهو خطي متماثل بدلاً من خطين. فضاء الجداء الداخلي هي فضاء متجه معياري، والجداء الداخلي للمتجه بحد ذاته حقيقي وإيجابي - محدد.

 الدوال

يتم تعريف الجداء النقطي للمتجهات التي لها عدد محدود من الإدخالات. وبالتالي يمكن اعتبار هذه المتجهات على أنها دوال متقطعة: طول - n متجه u، إذن، الدالة مع المجال {k ∈ ℕ ∣ 1 ≤ k ≤ n}, و u_i هي تدوين لصورة i بالدالة / المتجه u.

يمكن تعميم هذه الفكرة على الدوال المستمرة: تماماً كما يستخدم الجداء الداخلي في المتجهات مجموعاً فوق المكونات المقابلة، يتم تعريف الجداء الداخلي في الدوال على أنه جزء لا يتجزأ من بعض الفترات a ≤ x ≤ b (يُشار إليها أيضاً بـ [a, b]):

$\left\langle u,v\right\rangle =\int _{a}^{b}u(x)v(x)dx$

معمم كذلك على الدالة العقدية ψ(x) و χ(x)، عن طريق القياس مع الجداء الداخلي المعقد أعلاه، يعطي

$\left\langle \psi ,\chi \right\rangle =\int _{a}^{b}\psi (x){\overline {\chi (x)}}dx.$

 دالة الوزن

يمكن أن تحتوي الجداءات الداخلية على دالة وزن (أي دالة تزن كل مصطلح في الجداء الداخلي بقيمة). صراحة، الجداء الداخلي للدوال $u(x)$ و $v(x)$فيما يتعلق بدالة الوزن $r(x)>0$ يكون

$\left\langle u,v\right\rangle =\int _{a}^{b}r(x)u(x)v(x)dx.$

 الثنائيات والمصفوفات

لدى المصفوفات جداء فروبينيوس الداخلي، والذي يماثل الجداء الداخلي المتجه. يتم تعريفه على أنه مجموع جداءات المكونات المقابلة لمصفوفتين A و B لهما نفس الحجم:

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}{\overline {B_{ij}}}=\mathrm {tr} (\mathbf {B} ^{\mathrm {H} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {H} }).$

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}B_{ij}=\mathrm {tr} (\mathbf {B} ^{\mathrm {T} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {T} })=\mathrm {tr} (\mathbf {A} ^{\mathrm {T} }\mathbf {B} )=\mathrm {tr} (\mathbf {B} \mathbf {A} ^{\mathrm {T} }).$ (للمصفوفات الحقيقية)

لدى الثنائيات جداء نقطي وجداء نقطي مزدوج محدد عليها، راجع Dyadics § Product of dyadic and dyadic للتعرف على تعريفاتها.

 الموتّرات

الجداء الداخلي بين موتّر للمرتبة n وموتّر المرتبة m هو موتّر من المرتبة n + m − 2، راجع تقلص موتّر للحصول على التفاصيل.

 الحساب

 الخوارزميات

يمكن أن تعاني الخوارزمية المباشرة لحساب جداء النقطة العائمة للمتجهات من اختصار كارثي. لتجنب ذلك، يتم استخدام أساليب مثل خوارزمية جمع كاهان.

 المكتبات

يتم تضمين دالة الجداء النقطي في المستوى 1 BLAS.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضاً

• Cauchy–Schwarz inequality
• Cross product
• Dot product representation of a graph
• Euclidean norm, the square-root of the self dot product
• Matrix multiplication
• Metric tensor
• Multiplication of vectors
• Outer product

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Inner product", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Explanation of dot product including with complex vectors
• "Dot Product" by Bruce Torrence, Wolfram Demonstrations Project, 2007.