قاعدة الجداء

هذا المقال هو عن the derivative of a product. إذا كنت تريد the relation between derivatives of 3 dependent variables، انظر Triple product rule. إذا كنت تريد a counting principle in combinatorics، انظر Rule of product. إذا كنت تريد conditional probabilities، انظر Chain rule (probability).

Geometric illustration of a proof of the product rule

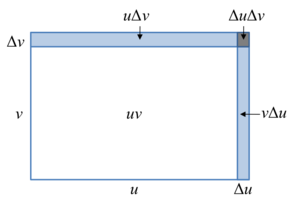
في التحليل الرياضي ، قاعدة الجداء ( و تدعى أيضا قانون لايبنتز) قاعدة تستخدم لحساب التفاضل لجداء توابع قابلة للمفاضلة :

لهذا يمكن ان نقول :

$(fg)'=f'g+fg'\,$

أو بترميز لايبنتز :

${d \over dx}(uv)=u{dv \over dx}+v{du \over dx}.$

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Geometric algebra

انظر أيضاً: Blade (geometry)

The term k-blade was used in Clifford Algebra to Geometric Calculus (1984)

Multivectors play a central role in the mathematical formulation of physics known as geometric algebra. According to David Hestenes,

[Non-scalar] k-vectors are sometimes called k-blades or, merely blades, to emphasize the fact that, in contrast to 0-vectors (scalars), they have "directional properties".

In 2003 the term blade for a multivector that can be written as the exterior product of [a scalar and] a set of vectors was used by C. Doran and A. Lasenby. Here, by the statement "Any multivector can be expressed as the sum of blades", scalars are implicitly defined as 0-blades.

In geometric algebra, a multivector is defined to be the sum of different-grade k-blades, such as the summation of a scalar, a vector, and a 2-vector. A sum of only k-grade components is called a k-vector, or a homogeneous multivector.

The highest grade element in a space is called a pseudoscalar.

If a given element is homogeneous of a grade k, then it is a k-vector, but not necessarily a k-blade. Such an element is a k-blade when it can be expressed as the exterior product of k vectors. A geometric algebra generated by a 4-dimensional vector space illustrates the point with an example: The sum of any two blades with one taken from the XY-plane and the other taken from the ZW-plane will form a 2-vector that is not a 2-blade. In a geometric algebra generated by a vector space of dimension 2 or 3, all sums of 2-blades may be written as a single 2-blade.

 أمثلة

Orientation defined by an ordered set of vectors.

Reversed orientation corresponds to negating the exterior product.

Geometric interpretation of grade n elements in a real exterior algebra for n = 0 (signed point), 1 (directed line segment, or vector), 2 (oriented plane element), 3 (oriented volume). The exterior product of n vectors can be visualized as any n-dimensional shape (e.g. n-parallelotope, n-ellipsoid); with magnitude (hypervolume), and orientation defined by that on its (n − 1)-dimensional boundary and on which side the interior is.

• 0-vectors are scalars;
• 1-vectors are vectors;
• 2-vectors are bivectors;
• (n − 1)-vectors are pseudovectors;
• n-vectors are pseudoscalars.

In the presence of a volume form (such as given an inner product and an orientation), pseudovectors and pseudoscalars can be identified with vectors and scalars, which is routine in vector calculus, but without a volume form this cannot be done without making an arbitrary choice.

In the algebra of physical space (the geometric algebra of Euclidean 3-space, used as a model of (3+1)-spacetime), a sum of a scalar and a vector is called a paravector, and represents a point in spacetime (the vector the space, the scalar the time).

 Bivectors

المقالة الرئيسية: Bivector

A bivector is an element of the antisymmetric tensor product of a tangent space with itself.

In geometric algebra, also, a bivector is a grade 2 element (a 2-vector) resulting from the wedge product of two vectors, and so it is geometrically an oriented area, in the same way a vector is an oriented line segment. If a and b are two vectors, the bivector a ∧ b has

• a norm which is its area, given by

  $\left\|\mathbf {a} \wedge \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\,\sin(\phi _{a,b})$

• a direction: the plane where that area lies on, i.e., the plane determined by a and b, as long as they are linearly independent;
• an orientation (out of two), determined by the order in which the originating vectors are multiplied.

Bivectors are connected to pseudovectors, and are used to represent rotations in geometric algebra.

As bivectors are elements of a vector space Λ²V (where V is a finite-dimensional vector space with dim V = n), it makes sense to define an inner product on this vector space as follows. First, write any element F ∈ Λ²V in terms of a basis (e_i ∧ e_j)_{1 ≤ i < j ≤ n} of Λ²V as

$F=F^{ab}\mathbf {e} _{a}\wedge \mathbf {e} _{b}\quad (1\leq a<b\leq n),$

where the Einstein summation convention is being used.

Now define a map G : Λ²V × Λ²V → R by insisting that

$G(F,H):=G_{abcd}F^{ab}H^{cd},$

where $G_{abcd}$ are a set of numbers.

 تطبيقات

Bivectors play many important roles in physics, for example, in the classification of electromagnetic fields.

 انظر أيضاً

• Blade (geometry)
• Paravector