ميكانيكا
يُعرِّف الميكانيك mechanics القواعدَ والشروط التي وفقها تحافظ الأجسام في الطبيعة على حالتها، أوتعدلها من السكون أو الحركة. وهو علم تجريدي في تطوراته وتجريبي في مبادئه الأساسية. كما أنه علم رياضي بحت ومجرد، له فرضياته ومسلماته الخاصة (التي تمليها الطبيعة عليه)، وهذا ما يلمس عند تشبيه النقطة المادية بالنقطة الهندسية، وعدّ الأجسام التي لها حجمٌ ما وكأنها أجسام اعتبارية صورية غير قابلة للتشوه. وينتمي علم الميكانيك إلى العلوم التجريبية عندما يتناول بالمعالجة مسائل الأجسام الصلبة الطبيعية والقابلة للتشوه، لكن حتى عند تطبيقه على الأجسام الصلبة الحقيقية، فإنه يبحث عن الحلول بطريقة استنتاجيّه مبنية على قاعدة أسس بسيطة وعامة، وبهذا يعود؛ لينضم لميدان العلوم العقلية، وليس لميدان العلوم الفيزيائية التي تعمل بطريقة استقرائية للوصول إلى البرهان0 وللملاحظة والتجربة فيه دور حاسم إذ يشتمل الميكانيك العقلي إضافة إلى الأسس العامة المهمة من نماذج وطرائق تقصٍّ (ولا سيّما نظرية المتجهات) على:[1]
- علم الحركة: الذي يدرس حركة الأجسام بتابعية الزمن.
- علم التحريك: الذي يدخل في دراسة حركة الأجسام مبدأ العطالة ومفهوم الكتلة والخواص الجوهرية الذاتية للمادة.
- علم السكون: الذي يدرس خصوصاً مسائل التوازن وشرط استقرار الأجسام في حالة الراحة (السكون)0
فروع الميكانيك
- ميكانيكا كلاسيكية Classical mechanics
- ميكانيك نيوتني, يمثل النظرية الأساسي في الحركة (علم الحركة (كينماتيكا) kinematics ) و القوى (علم التحريك (ديناميكا) Dynamics )
- ميكانيك لاغرانج Lagrangian mechanics ، شكلية نظرية للميكانيك .
- ميكانيك هاميلتوني Hamiltonian mechanics ، شكلية نظرية أخرى
- ميكانيك نجمي Celestial mechanics ، حركة النجوم ، و مجرات, .. الخ .
- علم التحريك الفلكي Astrodynamics, استكشاف الفضاء بالمركبات الفضائية.
- ميكانيك الأجسام الصلبة Solid mechanics ، مرونة Elasticity ، خواص الأجسام
- صوتيات Acoustics ، الصوت في الأصلاب و السوائل .. .
- علم السكون Statics ، الأجسام في حالة توازن .
- ميكانيك السوائل Fluid mechanics, يدرس حركة السوائل .
- ميكانيك استمراري Continuum mechanics ، ميكانيك المواد المستمرة (الأجسام الصلبة و السائلة)
- هيدروليك Hydraulics ، توازن السوائل .
- ميكانيك حيوي Biomechanics ، الأجسام الصلبة ، السوائل .. الخ ضمن الجسم الحي
- ميكانيك إحصائي Statistical mechanics ، تجمعات كبيرة من الجسيمات .
- الميكانيك النسبي العام
- ميكانيك الكم Quantum mechanics
- فيزياء الجسيمات, حركة و بنية و تفاعلات الجسيمات
- فيزياء نووية Nuclear physics ، الرحكة ، البنية ، ردود الفعل للنواة الذرية
- فيزياء المادة المكثفة Condensed matter physics ، غازات, أصلاب, سوائل كمومية .. الخ .
- ميكانيك إحصائي كمومي, التجمعات الكبيرة من الجسيمات
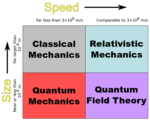
الكلاسيكية مقابل الكم
| ميكانيكا كلاسيكية | ||||||||
تاريخ...
| ||||||||
| جزء من سلسلة مقالات عن |
| ميكانيكا الكم |
|---|
النسبية مقابل نيوتن
تقدّم الميكانيك العقلي تدريجياً عبر الزمن وفقاً لطريقتين منفصلتين دون التوقف عن العمل بالطريقة الاستنتاجية: الطريق الأول هو الطريق التركيبي الذي اتبعه نيوتن خصوصاً على غرار علوم الهندسة القديمة التي كانت تسعى إلى اكتشاف القوانين والنظريات بتركيب الخواص الناتجة للإنشاءات المرسومة والأشكال الهندسية. ثم تطور الميكانيك بالبحث عن شروط وجود القوانين والنظريات، أو مميزات الأشكال وخواصها بطريقة الحساب الجبري وكما توجد هندسة تحليلية يوجد أيضاً ميكانيك تحليلي له مجال واسع؛ ليكون موضوع دراسة خاصة مثمرة ولا سيّما على قاعدة مبدأ الأعمال الافتراضية ومعادلات لاغرانج، وكذلك في البحث عن شروط توازن الأجسام واستقرارها.
النسبية العامة مقابل الكم
التاريخ
العصور القديمة
كانت إسهامات قدماء اليونان في تطوير علم الميكانيك قليلة. ففي مجال الميكانيك السماوي شارك كل من أرسطو وهيبارك وبطلميوس في تطويره إلى أن توصلوا إلى أن الشمس هي مركز الكون، وكانت الدراسات وقتئذٍ موجهة نحو علم الحركة. أما في الميكانيك الأرضي فكانت الأبحاث مكرسة لدراسة السكون وتوازن السوائل وضغطها؛ والتي عالجها أرخميدس الذي يعود له الفضل في تعريف مركز الثقل وقوانين توازن الروافع واكتشاف ما يعرف بدافعة أرخميدس. وفي الفترة الفاصلة بين القرن الأول والقرن الرابع للميلاد أجرى عدد من العلماء دراسات أولية لبعض الآلات المستخدمة في الورش «كالروافع والملفاف» (آلة رفع متعددة البكرات)0 وقد طرح أرسطو أفكاراً ونظريات في علم التحريك؛ منها أن كل جسم أرضي يبقى في مكانه ساكناً مالم يحرك من مكانه وعند إزاحته من مكانه بعنف يعود إليه بحركة طبيعية؛ والأكثر استقامة هو الأكبر سرعة؛ وأن كل حركة شديدة تحتاج إلى محرِك تعاكسه مقاومة. وقد ساد ميكانيك أرسطو فترة طويلة في الغرب حتى القرن الثالث عشر الميلادي.
العصر الإسلامي
أما في العالم الإسلامي فقد كانت لابن سينا وفخر الدين الرازي وأبي البركات هبة الله البغدادي وغيرهم (بين القرنين الحادي عشر والثالث عشر الميلادي) مساهماتهم القيمة في دراسة الحركات والقوى. فقد رأى ابن سينا «أن الجسم له ميل للاستمرار في حركته، يحس بها المانع الذي لا يتمكن من منع حركته إلا فيما يضعفها أولاً، إذ تأخذ الموانع الطبيعية والخارجية في إفنائها قليلاً». ويؤكد الرازي «أن القوة الطبيعية تزداد مع عظم الجسم، فالأجسام كلما كانت أعظم كان ميلها إلى إحيازها الطبيعة أقوى، فإذا كانت كذلك كان قبولها للميل القسري أضعف». ويتضح من كلام الرازي أن المقصود ازدياد القوة كلما كانت كتلته أكبر. وقد توصل البغدادي إلى ما يقابل مفهوم «التسارع» إذ يقول: «إن الجسم الذي يلازمه سبب حركته؛ تزداد حركته على التواصل لولا مقاومة الوسط، سواء أكانت حركته طبيعية أم قسرية»، كما توصل إلى ما يقابل قانون العطالة الذي قال به غاليليه بعد ما يقرب من 500عام: «إن الجسم الذي يفارقه سبب حركته يظل مستمراً في الحركة التي استفادها من القاسر لولا مقاومة الوسط من ناحية، ولولا سبب حركة طبيعية فيه إلى جهة خاصة من ناحية أخرى» (يقصد حركة السقوط بتأثير جاذبية الأرض).
العصور الوسطى
وفي القرن الرابع عشر ظهرت نظرية الاندفاع التي دافع عنها جان بوريدان (1300-1358): «يطبع المحرك على المتحرك اندفاعاً يتناسب طرداً مع السرعة، لكن مقاومة الهواء والجاذبية يضعِفان هذا الاندفاع بشكل تدريجي، وهذا يدعو الجاذبية إلى إعادة المتحرك إلى الأرض عندما يضعف الاندفاع وينتهي»0
بداية العصر الحديث
وتقدم علم الفلك في عصر كوبرنيك إذ حرر ثلاثة قوانين أساسية في علم الحركة للمجموعة الشمسية:
1- ترسم الكواكب في حركتها قطوعاً ناقصة تتوضع الشمس في أحد محرقيها (1609).
2- يمسح نصف القطر الشعاعي الذي ينطلق من الشمس إلى الكوكب سطوحاً متساوية في أزمنة متساوية (1609)0
3- يتناسب مربع زمن دوران الكوكب حول الشمس مع مكعب طول المحور الكبير للمدار (1619). وفي هذه الفترة اكتشف غاليليه الأقمار الأربعة لزحل (1610) مع اهتمامه بالفيزياء والميكانيك الأرضي خاصّة بعد أن اعتقد في بداية أبحاثه أن السرعة في السقوط الحر بدءاً من السكون تتناسب طرداً مع المسافة المقطوعة. لكنه عاد واعترف بلا معقولية هذا الفرض وأن السرعة تتناسب مع الزمن.
جاء بعد ذلك هويگنز Huygens الذي اكتشف القوة النابذة عام 1673. وطبق الحركة النوسية على الميقاتيات الدقيقة. في أثناء هذه الفترة من الزمن أعلن ديكارت عدة قوانين تتعلق بتصادم الأجسام، وكانت غالبيتها خاطئة. وقام العالم هوك (1635-1703) بتجارب عديدة في مجال الضوء والميكانيك، وكتب في عام 1680 إلى نيوتن: «إني أفترض أن التجاذب قائم دائماً بشكل متبادل ويتناسب مع مربع المسافة عن المركز». وقد رُفضت فرضيات هوك في كل من الضوء والميكانيك من قبل نيوتن الذي كان تلميذاً نبيهاً عند ديكارت في مجال الرياضيات البحتة. وقد عرف نيوتن قبل عام 1672 مكونات الضوء الأبيض. وفي مطلع عام 1685 قدّم إلى الجمعية الملكية في لندن مقترحاته الأساسية حول مؤلفه «المبادئ الرياضية للفلسفة الطبيعية»، وكان يقع في ثلاثة كتب، تناول أولها الأداة الرياضية لحساباته مع تطوير علم الميكانيك النظري المطبق على حركة الكواكب وتناول الكتاب الثاني دحض نظرية الاضطرابات الدوامية لديكارت وتفنيدها وإعادة تلك النظرية إلى الحركة في وسط مقاوم والمقاومة فيه تتناسب طرداً مع السرعة أو مربعها، أما الكتاب الثالث فكان أكثر فيزيائية من الكتابين الآخرين، وشمل مجموعة من تجاربه واختباراته الأرضية وملاحظاته الفلكية. وقد صاغ نيوتن كتاباته بأسلوب يختلف عن الأسلوب التحليلي الذي استخدمه ديكارت، وهو أقرب لأسلوب قوانين أرخميدس وأبولونيوس قبل الميلاد ودقّتها. وقد اتبع هذا الأسلوب بعض العلماء البريطانيين في القرن الثامن عشر. لكن سرعان ماعاد بعض الميكانيكيين الذين جاؤوا بعد نيوتن إلى الكتابة التحليلية الديكارتية المطوَّرة والمستخدمة في حساب اللامتناهيات في الصغر0 وكان من أشهر هؤلاء العلماء دالامبير وأولر (1707-1783). لكن دراسات هؤلاء العلماء كانت مبعثرة؛ وتنقصها المنهجية، فجاء لاغرانج ، وكان عمره وقتئذ لايتجاوز تسعة عشر عاماً؛ واكتشف المبادئ والأسس المهمة في الميكانيك؛ ومن بينها التغيرات العائدة لأولر ومبدأ السرع الافتراضية في علم السكون ومبدأ دالامبير. وصاغ لاغرانج جميع الأعمال المنتثرة هنا وهناك في كتاب واحد؛ هو الميكانيك التحليلي (1788)، وأشهر أعمال لاغرانج مايعرف بمعادلات لاغرانج وهي معادلات تفاضلية للحركة.
ومن ألمع خلفاء لاغرانج كان هاملتون(1805-1865)، وقد شرع في أبحاثه في كل من علم الضوء والميكانيك، وصاغ مجموعة من النتائج في الضوء الهندسي كانت قابلة للتفسير وفقاً لفهم هويجنز وقابلة للتفسير جسيمياً وفقاً لفهم علم الحركة في مبدأ الفعل الأصغري الذي يعرف بمبدأ هاملتون.
العصر الحديث
وأصبح الميكانيك التقليدي في بداية القرن العشرين مجموعة مترابطة يفترض مسبّقاً وجود المكان المطلق (الجملة المطلقة التي تنسب إليها الحركات كافة)؛ أي ما عرف بالأثير الذي قبل بوجوده كل من فرينل وماكسويل ولورنتز في مجال علم الضوء الموجي. بعد ذلك جاءت تجربة مايكلسون (1852-1931) في عام 1881 مناقضة لفرضية وجود الأثير، وأيدَ ذلك أينشتاين الذي أعلن فرضياته الشهيرة:
1- تبقى قوانين الظواهر الفيزيائية نفسها في جمل المقارنة المتحركة بالنسبة إلى بعضها حركة مستقيمة منتظمة0
2- ينتشر الضوء في الجملة المعتبرة بسرعة ثابتة مستقلة عن حركة المنبع الضوئي0
بقي الميكانيك التقليدي تقريباً أولياً في النظرية النسبية الخاصة والعامة عندما يمكن إهمال السرعات أمام سرعة الضوء.
جلبت فيزياء الذرة وكذلك الضوء أنواعاً أخرى من الميكانيك تختلف عن ميكانيك نيوتن. فنموذج بور للذرة الذي اقترح عام 1913 قاد إلى قبول أن الإشعاعات التي تصدرها الذرة ليست مستمرة، لكنها تنتج بطريقة منفصلة عندما يقفز الإلكترون من مدار مستقر إلى آخر. يرتبط هذا الإصدار بالفعل الكمومي (الكوانتي) الذي أدخله العالم بلانك في نظرية إشعاع الجسم الأسود عام (1900). وانطلاقاً من النظرية النسبية الخاصة ومن قانون بلانك أوجد لوي دوبري عام 1924 الميكانيك الموجي الذي وفقه يلازم بكل متحرك في حالة الحركة موجة طور، ومن هذه الدعوى استوحى شرودينغر عام 1926 بحثه عن العلاقة بين علم الحركة للجمل وظاهرة انتشار الأمواج.
وفي عام 1925 ظهر ميكانيك الكمّ لهايزنبرغ الذي أراد بالتماثل مع الميكانيك التقليدي تأسيس ميكانيك موافق للنظرية الكمومية. وقد أيقظت قراءة المذكرة الأصلية لهايزنبرغ عند بول ديراك فكرة أن المعادلات التقليدية للميكانيك التحليلي ليست خاطئة إطلاقاً، وإنما يجب تعديل العمليات الرياضية التي يمكن بوساطتها أن تستخلص النتائج الفيزيائية، مما يقتضي إيجاد خوارزميات جديدة. ومع ذلك فالميكانيك الموجي لدوبري والميكانيك الكمومي لهايزنبرغ هما - رياضياً - متكافئان. وعلى الرغم من ذلك فإنه مع التطور المعاصر لعلم الفلك من جهة وفيزياء الجسيمات من جهة أخرى يتتابع؛ ويستمر تاريخ الميكانيك منذ كبلر وغاليليو على الأقل، وهذا مثال رائع عن الجهد المستمر الجماعي في مجال التعاون العلمي.
أنواع الأجهزة الميكانيكية
جمل المقارنة واختبارها
يتطلب تعيين وضع الجسم المتحرك اختيار أجسام أخرى (أجسام القياس) يتم بوساطتها تعيين وضع الجسم. تسمى هذه الأجسام بأجسام المقارنة، وتُسمى جملة الإحداثيات المسندة إلى تلك الأجسام جمل المقارنة. وكان العالم كوبرنيك أول من لاحظ أن اختيار جمل المقارنة يؤدي دوراً مهماً في دراسة الحركات، واقترح جملة مقارنة دعيت جملة كوبرنيك مبدؤها هو مركز الشمس، ومحاورها الثلاثة موجهة نحو ثلاثة نجوم توصف بالنجوم الثابتة لبعدها الشاسع عن المجموعة الشمسية0 وقد استخدم نيوتن جملة كوبرنيك عند دراسة حركة الأجرام السماوية. وهناك جملة تشتق من جملة كوبرنيك، لكنها تحمل اسماً مغايراً، تدعى الجملة الساكنة0 وإلى جانب جملة كوبرنيك أو الجملة الساكنة؛ يمكن استعمال جمل أخرى ملائمة، فمثلاً تستخدم الجملة المرتبطة بالأرض عند دراسة حركة الأجسام القريبة من سطح الأرض؛ وفي هذه الحالة ينطبق مبدأ الإحداثيات المتعامدة على مركز الأرض، أما المحاور الثلاثة فإما أن توجّه إلى ثلاثة نجوم بعيدة؛ وإما أن تتماسك مع ثلاث نقاط من الكرة الأرضية. تسمى الجملة الأولى الجملة الأرضية اللادورانية، وتسمى الأخرى الجملة الأرضية الدورانية.
يدعى تسارع الأجسام المتحركة المنسوبة إلى جملة كوبرنيك بالتسارع المطلق، وتدعى المحاور بالمطلقة، والحركات هي حركات مطلقة. إن المعادلة الأساسية للحركة المطلقة هي المعادلة المتجهة (الشعاعية):
حيث m كتلة النقطة المادية، و→a تسارع النقطة المنسوب إلى المحاور المطلقة، و→F القوة المطبقة.
قانون العطالة والجمل العطالية
الجسيم الحرّ - أي الذي لا يخضع لأيّ تأثير متبادل - هو عملياً غير موجود. والجسيم الحرّ ينبغي أن يكون إما معزولاً تماماً، وإما أن يكون وحيداً في الكون. ينص قانون العطالة على ما يأتي: يتحرك الجسيم الحرّ دوماً بسرعة ثابتة المقدار والاتجاه؛ أي دون تسارع؛ وبتعبير آخر يمكن القول: إن الجسيم الحرّ إما أن يتحرك على خطّ مستقيم بسرعة ثابتة؛ وإما أن يكون ساكناً (سرعته معدومة)0 وكل جملة مقارنة يتحقق فيها قانون العطالة تسمى جملة المقارنة العطالية. في الواقع لا تكون أيّ جملة معزولة على نحو تام في الكون، لكن بسبب بعد النجوم الشاسع عن المجموعة الشمسية يمكن القبول بأن مركز ثقل المجموعة الشمسية يتحرك دون تسارع؛ وهذا يصحّ على جملة كوبرنيك.
الميكانيك الأرضي
لايتحقق قانون العطالة عند دراسة حركة الأجسام في جملة المقارنة المرتبطة بالأرض؛ لأنها ليست جملة عطالية؛ وذلك بسبب تفلطح الأرض ودورانها حول المحور المار من القطبين. فإذا كانت السرعة الزاويّة للأرض هي ω كان التسارع النابذ الناتج هو ω2 r cos λ حيث r نصف قطر الأرض وλ زاوية خط العرض للجسم الموجود على سطح الكرة الأرضية.
فعند قذف حجر من قمة برج عال نحو الأسفل مباشرة ينحرف عن اتجاه الجاذبية؛ لأن لتسارع الحجر المقذوف مركّبة لا تولدها قوة جاذبية الأرض، وإنما تعود إلى الحركة الدورانية اليومية للأرض. وكذلك فإن اتجاه المطمار يأخذ اتجاه محصلة القوتين الناتجتين من جاذبية الأرض والقوة النابذة. وبما أن الأرض ليست معزولة في الكون؛ لأنها تتبادل التأثير مع كل من الشمس والقمر حسب قانون التجاذب الكوني. فمثلاً قوة التجاذب الكوني بين الشمس والأرض تعطى بالقانون:
حيث M كتلة الشمس، وm كتلة الأرض، وR المسافة بين مركز الشمس والأرض وK ثابت التجاذب الكوني.
وبما أن القيمة العددية للنسبة
من رتبة 0.006، فإذا كان جسم كتلته μ موجوداً على الأرض؛ فإن قوة التجاذب بينه وبين الشمس هي F = 0.006μ (باعتبار أن مركز الأرض غير متحرك) وهذه القوة موجهة من مركز الشمس نحو مركز الأرض وقيمتها ضئيلة جداً. وأيضاً تكون قوة التجاذب بين تلك النقطة والقمر هي F = 0.012μ، وهذه القيمة أيضاً ضئيلة جداً. إن قوى التجاذب بين الأرض من جهة وكل من الشمس والقمر من جهة أخرى تشوِّه قيمة تسارع الثقالة واتجاهها.
تسارع الثقالة ( الثقالة)
إذا كانت نقطة مادية معلقة بنهاية خيط، وهي بحالة سكون؛ فإن مقدار كلٍ من سرعتها النسبية Vr وتسارعها النسبي يساوي الصفر.
فإذا كان ثقل النقطة المادية المذكورة هو P، وكتلتها m، كان:
حيث
تسارع جذب الأرض، وجهته باتجاه مركز الأرض و
التسارع النابذ. ويدعى
تسارع الثقالة واختصاراً الثقالة.
إن اتجاه ينحرف عن اتجاه مركز الأرض من النقطة المعتبرة بسبب وجود الحد الثاني في العلاقة أعلاه، ويأخذ اتجاه الشاقول الذي يتعين بوساطة المطمار.
تغيّر قيمة g حسب خط الطول (الزوال)
إن قيمة سرعة دوران الأرض الزاويّة معبّراً عنها بالجملة السغثية CGS (وهي الجملة التي يقاس فيها الطول بالسنتيمتر، والكتلة بالغرام، والزمن بالثانية) هي:
وفي العلاقة:
تقع المتجهات
في مستوى الزوال، ومن المهم معرفة تغيّر g وفقاً لخطوط الطول. وبما أنه عند القطب تكون قيمة المتجهة
معدومة؛ فإن التسارع يؤول إلى تسارع جذب الأرض Y أما عند مستوى خط الاستواء فتكون الثقالةg عمودية على خط القطبين0 في الواقع يكون منحى المتجهتين
ومن ثمّ محصلتهما هو منحى الخط القطري لدائرة خط الاستواء، وبما أن المتجهتين متعاكستان؛ فإن قيمة g هي:
g = γ - ω r
إن قيمة نصف قطر الأرض r معروف عادة من القياسات الجيوديزية، ويمكن أن تقاس g بوساطة النواس، حيث g= 983.2(C.G.S) عند القطب، وg = 978.1 C.G.S عند خط الاستواء. والقيمة المطلقة γ لتسارع الأرض ليست كما عند خط الاستواء، بل هي وحدة سغثية n981.1(C.G.S) كما عند القطبين؛ وهذا يعود إلى تفلطح الكرة الأرضية0
قياس الثقالة
يمكن أن تقاس الثقالة تجريبياً بوساطة النواس البسيط الذي هو كرة صغيرة معلقة بخيط عديم الوزن وغير قابل للامتطاط، ثبت طرفه الآخر بنقطة ثابتة0 في حالة الاهتزازات الصغيرة (السعات الصغيرة) يعطى دور النواس T - وهو الزمن الفاصل بين لحظتي مرور الكرة بنقطة واحدة من مسارها مرتين متعاقبتين وفي جهة واحدة (نوسة كاملة) - بالقانون:
حيث l ترمز إلى طول النواس، وg الثقالة الأرضية في مكان النواس0 ومن قياس الدور T يتم بسهولة حساب الثقالة g.
انظر أيضا
- Analytical mechanics
- Applied mechanics
- Dynamics
- Engineering
- Index of engineering science and mechanics articles
- Kinematics
- Kinetics
- Non-autonomous mechanics
- Statics
- Wiesen Test of Mechanical Aptitude (WTMA)
المصادر
- ^ محمد سعيد محاسنة. "الميكانيك". الموسوعة العربية. Retrieved 2012-04-10.
- ^
Walter Lewin (October 4, 1999). Work, Energy, and Universal Gravitation. MIT Course 8.01: Classical Mechanics, Lecture 11 (ogg) (videotape) (in English). Cambridge, MA USA: MIT OCW. Event occurs at 1:21-10:10. Retrieved December 23, 2010.
{{cite AV media}}: CS1 maint: unrecognized language (link)
قراءات للإستزادة
- Landau, L. D.; Lifshitz, E. M. (1972). Mechanics and Electrodynamics, Vol. 1. Franklin Book Company, Inc. ISBN 0-08-016739-X.
{{cite book}}: CS1 maint: multiple names: authors list (link)
وصلات خارجية
- iMechanica: the web of mechanics and mechanicians
- Mechanics Blog by a Purdue University Professor
- The Mechanics program at Virginia Tech
- Physclips: Mechanics with animations and video clips from the University of New South Wales
- U.S. National Committee on Theoretical and Applied Mechanics
- Interactive learning resources for teaching Mechanics
- The Archimedes Project