فضاء طوبولوجي
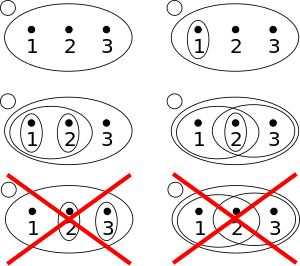
الفضاء الطوبولوجي (X,T) هو مجموعة X و نظام من مجموعات جزئية T ، تسمى مفتوحات X . النظام T (أو طوبولوجيا) يحقق الخصائص الآتية :
- المجموعة الفارغة و X ضمن T .
- تقاطع عناصر منتهية من T هو من T .
- الاتحاد (منته أم لا) لعناصر من T هو أيضا ضمن T .
أنواع للتوبولوجي التوبولوجي العام - التوبولوجي الهندسي - التوبولوجي الجبري - الطوبولوجيا الضبابية
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التعريف العام لعلم التوبولوجي
المعني اللغوي : وتنقسم الكلمة إلي مقطعين TOP) ومعناها المكان أو القمة OLOGY و معناها علم ) وهو علم دراسة المكان . المعني العلمي : هو هندسة الأشكال( الشرائح) المطاطية . وفرع التوبولوجي العام هو الركيزة الأساسية للدراسة والبحث المتقدم حيث أن هندسة اقليدس التي وضعت قبل الميلاد قد أرست دعائم التفكير المنطقي والعلمي بشكل معين , فإن علم التوبولوجي قد وسع دائرة الفكر لتكون أكثر مرونة ولتشمل العديد من الجوانب التي عجز التفكير أو الاتجاه الإقليدي عن معالجتها. و التوبولوجي هو العلم الجديد الذي يستخدم المرونة بدلاً من الحزم الاقليدي. والفضاء التوبولوجي هو نموذج رياضي مجرد للفضاء الكوني التي يدعونا الله عز جل إلي التفكير دائماً فيه أو دراسة ومحاولة وصف و التحكم في الظواهر الكونية , والتعامل مع كونه في صورته اللانهائية يعجز عنه قدرة البشر. وهناك بعض الاتجاهات الحديثة للنظر للبنية التوبولوجية علي أنها قاعدة أو أساس معرفي علي مجموعة من البيانات مستخلصة من تجارب في الحياة العملية , حيث إنشائها يعتبر بمثابة نموذج رياضي يمكن من خلاله استخراج خصائص جديدة لتجمع البيانات , وهذا الاتجاه في عصر المعلومات يُمكن الباحثين في جوانب الحياة المختلفة من إنشاء نماذج رياضية علي تجمعات كان من الصعب التعامل معها رياضياً . ووجود أكثر من بناء توبولوجي علي المجموعة يمكن النظر إليه علي أنه دراسة خصائص تجمع البيانات من خلال وجهات نظر للعديد من الخبراء بدلاً من خبير واحد وهذا يعطي نتائج أدق وطرق أخري لاستخلاص المعلومات .ولكي نقوم بصنع نموذج بنائي أكثر دقة فإن هذا النموذج لابد وأن يصنع من مميزات وخواص كل العناصر البنائية و قديما هناك كثيراً من العوامل المؤثرة تجعل صعوبة استخدام النماذج الرياضية ولا يمكن استخدامها والنظام الفازي قد جعل الخواص والصفات تشرح وتختبر تميز العناصر و العوامل للوظائف العضوية من خلال التجارب ونتيجة لذلك بالنظام الفازي يمكن الحصول علي نموذج إنساني ثابت يستخدم في حالات عديدة وينجز العديد من المهام المتعددة.
وأحدث اتجاه للمدرسة التوبولوجية إدخال المفهوم الفازي FUZZY SETS. وفي منتصف القرن التاسع عشر بدأت الرياضيات الحديثة بالظهور مع نظرية المجموعات لجورج كانتور التي بدأت وصف الظواهر الكونية وجبر المنطق الذي قدمه العالم بوول وبدأ التطبيق العملي لهذه المفاهيم في أنظمة فتح وغلق أجهزة الهاتف والدوائر الكهربية والمتغيرات في جبر بوول تأخذ القيمتين الصفر والواحد وهما يمثلان مرور تيار كهربي أو عدم مروره في دائرة كهربية وهي الآن تمثل عصب الشبكات الكهربية و شبكات الحاسب وفي العصر الحديث أعطي لطفي زادة الهندي الأصل مفهوم جديد يعطي وصفاً أكثر دقة للظواهر الطبيعية وهو مفهوم المجموعات الفازية (المشوشة ) والتي تعطي درجات الانتماء في الفترة المغلقة التي تحتوي علي الصفر والواحد وكان علم التوبولوجي هو اللبنة الأولي لتطبيق المفهوم الفازي وجهود العلماء تتوالي عاماً بعد عام لتقديم معرفات ومفاهيم جديدة وأول من طبق وأدخل هذه المفاهيم المدرسة التوبولوجية المصرية التي أرسي قواعدها العالم الجليل المرحوم الأستاذ الدكتور علي سالم مشهور عليه رحمة الله وحامل لواء علمه الأستاذ الدكتور محمد عزت عبد المنصف عميد كلية العلوم جامعة طنطا وأستاذ الرياضيات البحتة وطلابه الذين أعطوا الكثير والكثير ويشهد علي ذلك الموسوعات العلمية في مجال الرياضيات البحتة والتطبيقية. وخير شاهد علي هذا ما نشر مؤخراً عام 1998 في مؤتمر باليابان أن أكثر من 50 % من الأبحاث المقدمة في هذا المؤتمر العالمي تعتمد علي مفهوم واحد فقط من المفاهيم التي أدخلها العالم الجليل المتواضع الأستاذ الدكتور محمد عزت ومدرسته العلمية وقد غزت المدرسة التوبولوجية أنحاء العالم كله بالأبحاث العلمية والتطبيقية المختلفة وللأسف إعلامنا العربي غافل عن إبراز دور هذه المدرسة في خدمة العلم و هذه المدرسة العريقة التي يجب علي جميع التخصصات من مختلف فروع العلم التعاون مع هذه المدرسة لكي يجدوا ضالتهم وذلك لخدمة البشرية . وامتد ذلك للعلوم الأخرى مثل علوم الحاسب ( المترجمات – الذكاء الاصطناعي والنظم الخبيرة – أنظمة التحكم ) وعلم البيولوجي والاقتصاد وحتى الجغرافيا.
وأحدث رسالة دكتوراه في هذا الاتجاه التي قدمت ونوقشت في جامعة طنطا هي بعنوان : المثاليات في الفراغات التوبولوجية الفازية وتعتبر إضافة علمية جديدة للمدرسة التوبولوجية المصرية وبناء جديد في الفضاءات التوبولوجية الفازية عن طريق المفهوم الجديد المثاليات الفازية . وهي تفتح أبواب البحث في حلول مشاكل علمية معقدة لظواهر كونية لم تكن معروفة من قبل كما قال العالم المصري د. محمد النشائي رئيس قسم الفيزياء النظرية بجامعة كمبريدج ورئيس تحرير أكبر مجلة علمية Chaos تصدر في بريطانيا وأمريكا وهولندا و المرشح لجائزة نوبل في العلوم حيث أنه مكتشف العلم الجديد علم الشوشرة ونشرت بعض أبحاث هذه الرسالة في انجلترا و نشرت أبحاث آخري في الهند و أبحاث قدمت في المؤتمر السعودي الأول للعلوم و نشرت في مجلة اللقاء السادس لجمعية العلوم الرياضية السعودية و امتداداً لأحد تطبيقات هذه الرسالة :
اتجاه جديد وأبحاث تطبيقية في علم الهندسة الوراثية عن طريق التوبولوجي : وحيث أن الفراغ التوبولوجي الفازي يمكن النظر إليه هندسياً علي أنه حالة مجردة للشكل الهندسي وللفضاء الكوني بوجه عام , ولذلك فإن الدوال بين الفضاءات يمكن النظر إليها علي أنها تحويلات للأشكال الهندسية أو تغيرات تطرأ علي خصائص الفضاء ,ولذلك دراسة الدوال تساعد علي معرفة خواص هذه الفراغات وبناء أو تخليق فراغات جديدة ُمشتقة من الأنواع القديمة . لتطبيق التوبولوجي نختار المكان وهو الخلية الحية . في الحقيقة عندما قرأنا عن الخلية الحية هناك تصور من وجهة النظر التوبولوجية نجد أن الخلية الحية بمكوناتها تحقق شروط الفراغ التوبولوجي وعلي مدي علمي أن الحامض النووي (DNA ) يقع داخل النواة وأعرف أن دور الهندسة الوراثية هو توليد أحماض نوويةDNA جديدة دراسة إمكانية علاج الأورام السرطانية فيمكن أيضاً إثبات أن مكونات النواة فضاء توبولوجي أخر وأيضاً الخلية السرطانية فضاء توبولوجي مختلف طبيعته عن الفضاء التوبولوجي للخلية الحية ولإثبات ذلك بالنمذجة الرياضية لابد من وجود نظام خبير (نظام فازي) يحمل قواعد بيانات مفصلة عن مكونات الخلية الحية والحمض النووي DNA( النظام الفازي (FUZZY SYS. يعطي وصفاً أكثر دقة لتفسير الظواهر فهو يعطي درجات دقيقة للانتماء وعدم الانتماء . وبالتالي يمكن تعريف دالة توبولوجية تحمل خصائص الحمض النووي (DNA ) من النواة (الفضاء التوبولوجي الأول) إلي الخلية السرطانية ( الفضاء التوبولوجي الثاني ) تحت شروط حدية معينة بحيث تؤثر هذه الدالة علي مكونات الخلية السرطانية وتحويلها إلي خلايا ليس لها أي دور مؤثر علي الخلية الحية أو تعريف دالة توبولوجية أخري من الخلية السرطانية المتكونة إلي الخلية الحية وتحويل مكوناتها إلي مكونات مفيدة في الخلية الحية .
تطبيق بعض المفاهيم التوبولوجية :
مفهوم التغليق والانفتاح الإحكام والانفصال : في الفراغات التوبولوجيةٍ فتوسيع وتضيق الخلية والتحكم في محتواها يتم من هذا المفهوم .ويمكن استخدام مفهوم الداخلية بتصغير الخلية السرطانية حتى تتلاشي وتصل إلي .
عمل نظام خبير في الخلية الحية يمكن استخدام النظام الفازي واحدي لغات الذكاء الاصطناعي في عمل نموذج رياضي ونظام خبير أو قاعدة بيانات DATABASE في الأجزاء المكونة للخلية والقواعد المكونة للحمض النووي. فمن الأساليب الحديثة لاستخلاص المعلومات من البيانات وهندسة الأنظمة والذكاء الاصطناعي استخدام جميع النتائج في الفضاءات التوبولوجية الفازية في استحداث أساليب جديدة لاستخراج البيانات من المعلومات السابقة عن الخلية الحية والأحماض النووية .
طالع أيضاً
- T0 space
- T1 space
- Hausdorff space (T2)
- Completely Hausdorff space
- Urysohn space
- T3 space
- Tychonoff space
- Normal Hausdorff space (T4)
- Completely normal Hausdorff space (T5)
- Perfectly normal Hausdorff space (T6)
المصادر
د.أحمد عبد الخالق سلامة http://knol.google.com/k/-/spssmaple/2cp2vayd4io2e/1#
المراجع
- Armstrong, M. A.; Basic Topology, Springer; 1st edition (May 1, 1997). ISBN 0-387-90839-0.
- Bredon, Glen E., Topology and Geometry (Graduate Texts in Mathematics), Springer; 1st edition (October 17, 1997). ISBN 0-387-97926-3.
- Bourbaki, Nicolas; Elements of Mathematics: General Topology, Addison-Wesley (1966).
- Čech, Eduard; Point Sets, Academic Press (1969).
- Fulton, William, Algebraic Topology, (Graduate Texts in Mathematics), Springer; 1st edition (September 5, 1997). ISBN 0-387-94327-7.
- Lipschutz, Seymour; Schaum's Outline of General Topology, McGraw-Hill; 1st edition (June 1, 1968). ISBN 0-07-037988-2.
- Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.
- Runde, Volker; A Taste of Topology (Universitext), Springer; 1st edition (July 6, 2005). ISBN 0-387-25790-X.
- Steen, Lynn A. and Seebach, J. Arthur Jr.; Counterexamples in Topology, Holt, Rinehart and Winston (1970). ISBN 0-03-079485-4.
- Willard, Stephen (2004). General Topology. Dover Publications. ISBN 0-486-43479-6.
http://knol.google.com/k/-/extensions-of-fuzzy-ideals/2cp2vayd4io2e/12# Some fuzzy topological operators via fuzzy ideals Some fuzzy topological operators via fuzzy ideals http://www.ingentaconnect.com/content/els/09600779/2001/00000012/00000013/art00228;jsessionid=3lu5ndrnwf31r.alice?format=print