سيبرنيتيك
السيبرنيتيك Cybernetics هو علم حديث نوعيا ظهر في بداية الأربعينيات من القرن ال20 و يعتبر الرياضي نوربرت فينر من أهم مؤسسيه و قد عرف فينر السيبرنيتيك على أنها علم القيادة أو التحكم (control) في الأحياء و الآلات و دراسة آليات التواصل communication في كل منهما.
تاريخ السيبرنيتيك
المصدر اللغوي: سيبرنيتيك أو كيبرنتيك هي مفردة مشتقة من اللغة الإغريقية القديمة من كيبرنتيس أي القائد أو قائد السفينة كما قد تكون مشتقة من كيبرنتيكا أي فن قيادة السفن أو من كيبرنيسيس أي منصب قيادي في الكنيسة.
المصدر الإصطلاحي الحديث: السيبرنتيك هو علم القيادة أو التحكم (control) في الأحياء و الآلات و دراسة آليات التواصل communication في كل منهما.
بما أن فعل القيادة أو التحكم و فعل التواصل أو التخاطب قديمان قدم التاريخ الإنساني فإنه ليس من الدقة القول أن السيبرنيتيك علم حديث و هنا لمحة عن بعض الآلات التي إستعمل عند إختراعها مفاهيم سيبرنيتيكية دون أن تعرف هذه المفاهيم كسيبرنتيكية أو حتى أن يذكر اللفظ سيبرنيتيك:
في 300 ق م أخترع أول قنديل زيتي يحتوي على آلية تحكم
في 100 ق م إخترع هيرون الإسكندري آلية لفتح أبواب المسارح بطريقة أوتومتيكية
في 1784 م إخترع جيمس وات أدات لتعديل أو التحكم في سرعة دوران الآلة البخارية
إلخ ...
أما لفظة السيبرنتيك في مفهومها الحديث فقد أستعملت لأول مرة من قبل عالم الرياضيات الأمريكي نوربت فينر الذي عرف السيبرنتيك وأعطاها مفهومها الإصطلاحي الحديث للمزيد إضغط هنا .
إن بدايات السيبرنيتيك الحديثة كانت في المجال التقني ولعل ذلك أحد أسباب صعوبة إقحام هذه المادة في العلوم الإنسانية.
أهم مصطلحات السيبرنيتيك و فلسفتها
من أهم الإختلافات بين نظرة السيبرنيتيك إلى المشاكل و غيرها من الطرق هو أن السيبرنتيكي يفكر دائما في إطار النظم أو النظام أو المنظومات أي systems هذه النظرة تميزه عن غيره. حيث أنه يحاول أن يجرد الإشكال و ذلك يكون عادة عبر الخطوات التالية:
- تحديد حدود المنظومة التي يراد درسها. المنظومة تستطيع أن تكون مادية أو غير مادية أي متخيلة و حدودها أيضا
- وصف المنظومة أو القوانين التي تحكمها بالرياضيات عادة و بأي طريقة أو لغة تسمح بقدر ما من الحساب وذلك في مفهوم أوسع. هذه الخطوة تعرف بخطوة بناء النموذج من المنظومة Model building أو النمذجة
- إجراء الدراسات على إعتمادا على النموذج
كما أن السيبرنتيكي يفرق بين المجموعة و المنظومة. النظرة هنا قريبة إلى التيار المعروف بالتيار التوصيلي connectinism التي تقول أن الوظيفة أي وظيفة نظام ما تنتج عن الديناميكية أو العلاقات بين أجزائه. هذه الفكرة مطبقة مثلا بشكل كبير في الشبكات العصبونية
مثال على الفرق بين المجموعة و المنظومة
فلنأخذ الإنسان مثلا و ننظر إليه من الناحية البيولوجية فهو يمكن إعتباره مجموعة من الأعضاء كالقلب و الكبد و الرئة إلخ لكن السبيرنتيكي و على الصعيد البيولوجي سيعارض هذه الفكرة حيث أنك إذا جمعت الأعضاء الآنفة الذكر فإنك لن تتحصل على كائن حي فبالنسبة إليه المنظومة أي الكائن الحي إنسان هو أكثر من مجرد مجموع العناصر المكونة. ويمكن تعميم هذه الفكرة على منظومات أخرى و نظرات أخرى.
الأسس الرياضية للسبرنتيك
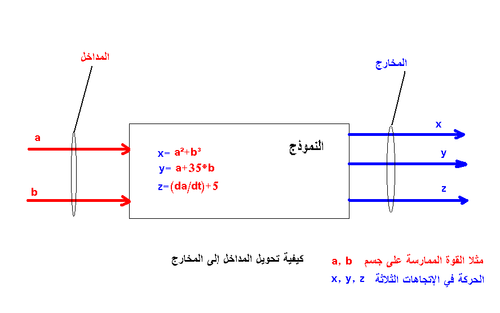
باالنسبة للنظم التقنية فإن اللغة الأكثر شيوعا لوصف أو بناء النموذج هي الرياضيات أما في ما يخص النظم الأخرى فإن إستعمال الرياضيات بقي محدودا نوعا ما. من أهم المصطلحات الرياضية في السيبرنتيك هو مصطلح التحويل أو دالة التحويل (transfer Functions) أي كيف تحول المداخل إلى المخرج حيث المداخل و المخارج يمثلان كميات فزيائية أو خصوصيات. و مصطلح التوصيل الدائري أو الإرجاعي closeed loop.
أنواع النظم أو المنظومات
يمكن تقسيم النظم على عدة أسس:
- نظام ملموس كالصاروخ أو الإنسان أو المنظومة الشمسية او غير ملموس كالنظام المصرفي أو النظام الإشتراكي
- على أساس المعادلات التي تصف النموذج:
- نظم خطية و هي الأسهل معالجة رياضيا linear
- نظم غير خطية و لا يوجد لمعالجتها طريقة عامة non linear
- نظم ترتبط فيها الخاصية المدروسة بالزمن فقط أي أن التغير في الزمن فقط differential equation
- نظم ترتبط فيها الخاصية المدروسة بالزمن و المكان partial differential equations
- نظم تكون فيها الخاصية المدروسة متصلة أي غير متقطعة continous
- نظم تكون فيها الخاصية المدروسة متقطعة discrete
- نظم ذات مدخل واحد و مخرج واحد single input single output أو سيزو
- نظم ذات عدة مداخل و عدة مخارج multiple input multipl output أو ميمو
- نظم ذات نموذج غير معروف أو ما يسمى بالصندوق أسود BlackBox أو ذات نموذج معروف أي صندوق زجاجي GlassBox
الحساب بالنظم
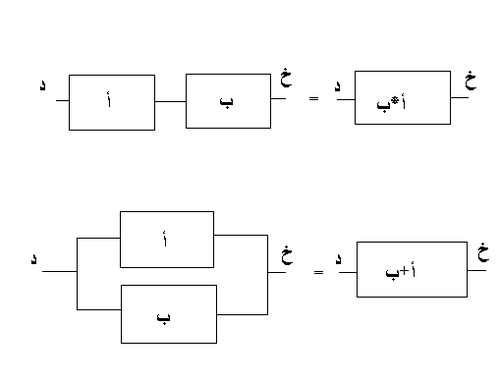
إذا إعتبرنا د و خ مداخل و مخارج المنظومة و أ و ب دالة التحويل النظام وإذا ربطنا النظم أ و ب كما هو مبين في الصورة فإن دالة التحويل تصبح كما هو مبين أسفله.
لفظة أو مفهوم التحكم
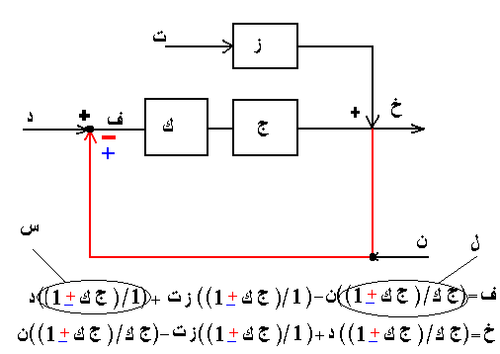
لنفترض أنه لدينا نظام ك×ج أيا كان نوعه تقني أو بيولوجي أو غيره و لنفترض أن لهذا النظام مدخلا واحدا د و مخرجا واحدا خ أي أنه نظام سيزو. التحكم في نظام كهذا يعني أننا نريد أن نتحكم في مخرج النظام و على أساس ذلك فإننا نعطيه أو نزود مدخله بالقيمة التي نريدها لمخرجه. و لمزيد من التدقيق لندرس النظام الموضح أسفله وهو نظام يمكن إعتباره كمثال عام لكل الأنظمة المتحكم فيها حيث أن النظام موصول دائريا closed loop أي أن خارجه يعاد و يوصل بمدخله كما هو موضح بالسهم الأحمر
حيث نعتبر
- ج×ك النظام المراد دراسته حيث ك هو المتحكم أي الcontroller أو ال governor
- د و خ المدخل و المخرج
- ت تشويشا عند المخرج
- ن تشويشا في قياس المخرج أو المتحكم فيه
- ف الفرق بين القيمة التي نريدها للمخرج و القيمة الحقيقية له
- ز دالة تحويل التشويش عند المدخل وهي غير مهمة
إذا إعتبرنا ذلك فإن دالات التحويل تكون كما هو مبين في الصورة أعلاه وهي دالات يسهل إشتقاقها إذا ما إستعملنا عمليات الحساب بالنظم. نلاحظ أول مشكلة تعترضنا حيث أننا نريد أن تكون المخارج مساوية للمداخل ولكن دون تشويش أي أننا نريد
خ = د
و هذا يعني أننا نريد ج ك/ ج ك + 1 أن تكون 1 ولكن هذه مشكلة لأن ذلك يعني أن دالة تحويل التشويش هي واحد أيضا وهذا ما لا نريده.
كما نريد
ف = 0
أي أن تكون الدالتان صفرا ولكننا لا نريد لدالة تحويل المدخل للمخرج أن تكون صفرا. لقائل أن يقول لماذا لا نتحكم في المدخل حتى يكون ضاربه في ج ك/ ج ك + 1 يساوي عكس الباقي. لا تنسى أن الهدف من التحكم هو أن يتغير المخرج طبقا لما نريده لا أن نحاول إيجاد مدخل يكون الفرق فيه صفرا. المشكل الثاني هو أنك لا تستطيع تغيير س بدون تغيير ل و ذلك لإن س + ل يساوي 1 و يمكن التأكد من ذلك بعملية حسابية بسيطة.
الحل:
عادة ما تكون ترددات أي frequency التشويش زت أي ت منخفضة
و ترددات ن مرتفعة
و ترددات د منخفضة
ولذلك فإن على دالات التحويل أن تكون كما هو موضح في الصورة أسفله
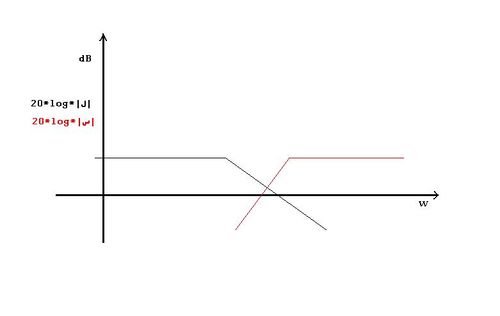
و الصورة عبارة عن مخطط خاص حيث يرسم على إحدى الإحداثيات التردد و على الآخر قوته ( بالديسيبال). وفي الرسم المبين أعلاه نستطيع أن نرى أن لكل تردد تقوية أو ضارب خاص أي أنك إذا و ضعت في المدخل إشارة يكون ترددها 1 هرتز و قوتها (Amplitude) خمسة مثلا فإن المخرج سيكون إشارة بقوة 1 هرتز (إذا كانت التقوية أو الضارب 1:5 مثلا) أما إذا وضعنا في المدخل إشارة بتردد 13.092 هرتز مثلا فسيكون الضارب مغايرا(ضارب 1 نثلا) و يكون المخرج إشارة بقوة قدرها قدر قوة المدخل. مثال(رياضي): المدخل = (a*cos(w*t+p حيث a قوة التردد w التردد
المخرج يساوي (G(w)*a*cos(w*t+p
الفرق بين التسيير و التحكم
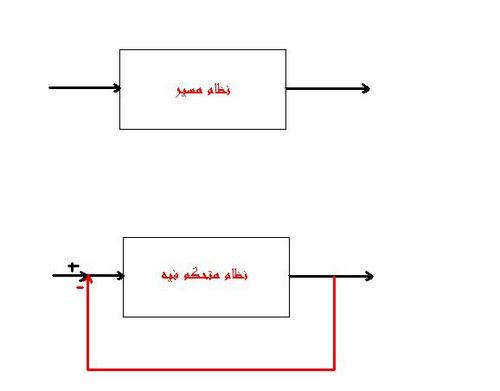
عادة ما يكون هناك تفريق بين النظام الموصل دائريا closed loop و النظام الموصل أماميا open loop control(أنظر الصورة)
مفهوم الإستقرار(stability)
تكون حالة نظام ما مستقرة إذا كان النظام يعود دائما إلى هذه الحالة إذا أبعدناه(في حدود معينة) عنها أو أنه يبقى في هذه الحالة إن لم نؤثر عليه
- مثال:
خذ عصا و حاول مسكها من طرفها سوف تشير العصا إلى الأسفل لأن هذه الحالة مستقرة و لكن إذا وضعت العصا على كفك و أردت أن تشير بها إلى الأعلى فإنك تلاحظ أن العصا تنفر من هذه الحالة و تبتعد عنها في إتجاه الحالة المستقرة.
- أهمية الإستقرار: لنؤخذ مثلا درجة حرارة الجسم مثلا فهي يجب أن تكون 37 درجة و هي حالة مستقرة أي أنه إذا أبعدنا أجسامنا عن هذه النقطة(37 درجة) بتعرضنا لحرارة الشمس فإن آلية التحكم تجعل الجسم يفرز العرق للتبريد فنعود إلى درجة حرارة 37 فتخيل إذا كانت هذه الحالة غير مستقرة ماذا سيحدث
- مثال ثاني من المجال الهندسي: في علم بناء الجسور يجب إجراء دراسة لكيفية تعامل الجسر مع الذبذبات التي يحدثها المارة فإذا كانت دالة تحويل الجسر غير مستقرة فإنه بالإمكان أن تهدم الجسر بمجرد أنك تمشي عليه و تحدث ترددا يوازي التردد الذاتي للجسر. وهنا أريد أن أذكر نكتة حيث تفطن الرومان القدامى لهذه الظاهرة(دون دراستها طبعا) فكانوا يعطون الأوامر لجنودهم بتغيير مشيتهم عند عبور الجسور.
و توجد عمليات رياضية معقدة لحساب إن كان نظام ما مستقر أم لا معضمها يتلخص في أن القيمة الذاتية لنظام ما يجب أن تكون سالبة.للمزيد إضغط هنا
مواضيع متعلقة
- تحويل فوريي
- تحويل لابلاس
- مفهوم الإستقرار
- التحكم المنبسط flatness based control
- التحكم بالنموذج الداخلي (internal model control (imc
- مصفوفة
- مصفوفة جاكوبي
- التخطيط بمعنى linearisation
- مفهوم الإنبساط
- أنواع الكونترولر
- مصفات كالمان
| تحرير | الحقول الفرعية و العلماء البارزين في مجال السيبرنتيك |
|---|---|
| مستوى أول | تعددية السياق Polycontexturality , سيبرنتيك الرتبة الثانية |
| مستوى ثان | نظرية الكوارث, الإتصالية, نظرية التحكم, نظرية القرار, نظرية المعلومات, سيميوتيك, سينيرجيتيك, نظرية الأنظمة |
| مستوى ثالث | سيبرنتيك بيولوجي, سيبرنتيك طبي حيوي, روبوتات حيوية, علوم عصبية حاسوبية, Homeostasis, سيبرنتيك طبي, سيبرنتيك عصبي, سيبرنتيكيات اجتماعية |
| علماء السيبرنتيك | ويليام روس أشبي, كلاود بيرنارد, فالينتين برايتنبيرغ, لودفيغ فون بيردالاندفي, جورج كاندي, جوزيف ج. ديستيفانو الثالث, هاينز فون فورستر, تشارلز فرانسوا, جاي فوريستير, ارنست فون غلاسيرسفيرد, فراسيس هيليغين, إيريش فون هولست, Stuart Kauffman, نيكيلاس لومان, فارين مككولوش, Humberto Maturana, Horst Mittelstaedt, Talcott Parsons, Walter Pitts, Alfred Radcliffe-Brown, Robert Trappl, Valentin Turchin, Francisco Varela, Frederic Vester, John N. Warfield, Kevin Warwick, نوربيرت فينر |