رنين

هذا المقال هو عن الرنين في الفيزياء. إذا كنت تريد الاستخدامات الأخرى، انظر رنين (توضيح).

"Resonate" redirects here. For other uses, see Resonate (توضيح).

"Resonant" redirects here. For the phonological term, see Sonorant.

Increase of amplitude as damping decreases and frequency approaches resonant frequency of a driven damped simple harmonic oscillator.

الرنين أو التجاوب المغناطيسي resonance هو ظاهرة مألوفة،

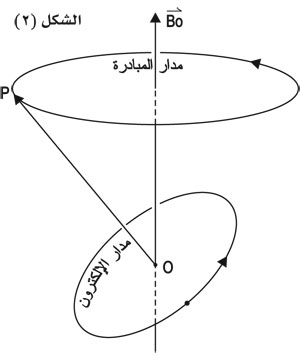
• الرنين من اكتشاف جاليليو جاليلي أثناء أبحاثه عن النواس بدءا من 1602. وتشاهد في جمل ميكانيكية أو كهربائية أو مغنطيسية. وتتلخص بأن يكون للجملة تواترٌ ذاتيٌّ (f0) حين تقوم بحركة دورية، وتستطيع أن تغيِّر طاقتها إذا أثّر فيها وسيط خارجي تأثيراًدوريّاً أيضاً. وحين يكون تواتر هذا الوسيط الذي يزوِّد الجملة بالطاقة يساوي تواترها الذاتي يتحقق شرط التجاوب، ويكون امتصاص الجملة للطاقة أعْظمياً. إن مثال الأرجوحة ودفعها دفعات بصورة دورية يتفق مع دورها فتزداد سرعتها زيادة كبيرة، نموذج لل التجاوب الميكانيكي، والوشيعة والمكثفة مثال عن التجاوب الكهربائي، وكلاهما يمكن ردّه إلى تغيرات في وسيط واحد أو مقدار عددي. أما التجاوب المغنطيسي magnetic resonance فيتعامل مع متَّجهات (أشعة). تُمثِّل هذه المتَّجهات اتجاهات مغانط صغيرة أو ما يعرف بعزوم ثنائيات القطب، وهي التي تملك التواترات الذاتية عندما يطبق عليها حقل مغناطيسي. إن استجابة المغنطيس الصغير (كالبوصلة) حين يؤثّر فيه حقل مغنطيسي ثابت في البدء تكون اهتزازية حول موضع توازنه، أمّا عندما يكون هذا المغنطيس من مرتبة الذرّة وفي الفضاء فإن تأثير الحقل يجعله يطوف أو يبادر precession حول الاتجاه الثابت بتواتر يتناسب مع شدّة الحقل يسمى تواتر المبادرة أو تواتر لارمور Larmor، وهو التواتر الذاتي للجملة المغنطيسية المدروسة. وإذا طُبِّق حقل مغنطيسي آخر عمودي على الحقل الأول ، يتغيَّر بصورة دورية فإن هذا الحقل الجديد هو الوسيط الذي سيغير طاقة الجملة وبالتالي سيغيّر من اتجاه الطواف في هذه الحالة. وعندما يتساوى التواتران يتحقق شرط التجاوب أي تمتص الجملة طاقة عظمى. وتعد الدوّامة أو الخذروف gyroscope المقابل الميكانيكي التقليدي لهذه الجملة. فإذا ما تخيَّلنا محور دوران الخذروف هو متجهة رأسها نحو الأعلى فإننا نلاحظ كيف ترسم النهاية العليا دائرة حول المحور الشاقولي نتيجة تأثير عزم الثقل أو عزم قوة الجاذبية الأرضية الذي يجعله يطوف (يبادر) وعلينا تطبيق قوة عمودية أخرى لتغيير اتجاه محور الدوران.

• وتحدث ظاهرة الرنين لكافة أنواع الاهتزازات والموجات. وهناك رنين ميكانيكي ورنين صوتي شوكة رنانة ورنين عمود الهواء في آلة الناي أو الأرغول الموسيقية. أو رنين كهرومغناطيسي في دائرة رنين، وكذلك رنين للموجات الكمومية. ويمكن استخدام أنظمة الرنين لتوليد اهتزازات عند تردد محدد، أو التقاط ترددات محددة من وسط حزمة اهتزازات تضم العديد من الترددات.

بدأت ظاهرة التجاوب المغنطيسي تحتل مكاناً مرموقاً في التطبيقات الفيزيائية والكيماوية حين طبقت على نوى الذرات التي لها عزم مغنطيسي وعرفت باسم التجاوب المغنطيسي النووي NMR: Nuclear Magnetic Resonance، كان ذلك عام 1940 على يد فيلكس بلوخ F.Bloch وويليام هانسن W.Hansen ومارتن بيكرد M.Bakerd في الولايات المتحدة وعلى يد إدوارد بيرسل E.Purcell وروبرت باوند R.Pound وهنري توري H.Torry في الوقت نفسه. ثم طبقت واكتشفت في إلكترونات الذرات التي تدور حول النواة، إذ تولّد الإلكترونات ذات الشحنة السالبة عند دورانها حول النواة حقلاً مغنطيسياً يمكن تمثيله بمغنطيس صغير عزمه ، وهو ما يسمى العزم المغناطيسي المداري. وكذلك فإن للإلكترون عزماً مغناطيسياً ذاتياً يسمى السبين (spin أو عزم اللف الذاتي). وعندما يكون هذا الأخير هو الجزء الفعّال في الجملة المدروسة يسمى التجاوب: تجاوب السبين الإلكتروني .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التطبيقات

قفزت تطبيقات هذه الظاهرة قفزات واسعة خاصة حين بدأ استعمالها لتعرُّف محيط بعض الذرات كالهيدروجين والكربون في الأنسجة الحية. وقد ترافق هذا الاستعمال مع معالجة النتائج بالحاسوب فصار بالإمكان استناداً إلى ظاهرة التجاوب هذه تصوير أجزاء مختلفة من جسم الإنسان استناداً إلى تراكيز هذه الذرات في الأنسجة المختلفة، دون تعريضها للأشعة السينية المؤذية فظهر ما يعرف باسم التصوير بالتجاوب المغنطيسيMagnetic Resonance Imaging اختصاراً (MRI) وصار الجهاز المستخدم معروفاً باسم «المرنان».

يكون الحقل المغنطيسي الناتج عن شحنة متحركة عمودياً على مستوى الحركة ويرتبط بمقدار الشحنة وسرعتها وموقعها من النقطة التي يقاس عندها الحقل، لذلك يمثل المغنطيس الصغير المقابل لإلكترون يدور في ذرة تبسيطاً بعزم مغنطيسي عمودي على مستوى حركته التحريك الكهربائي. ويوجد في الميكانيكا مقدار مشابه يصف الحركة الدورانية لجسم ما وتأثّرها بعزم القوة المطبق على الجسم هو العزم الزاوي، أو عزم الاندفاع anguler momentum الذي يرتبط بكتلة الجسم وسرعته وموقعه من محور الدوران وهو عمودي أيضاً على مستوي الحركة (الشكل ـ1). لذلك هناك نسبة ثابتة بينهما تسمى النسبة الجيرومغناطيسية.

في الواقع يتطلب معالجة سلوك الإلكترونات في الذرات وكذلك سلوك الذرات والجزيئات استعمال ميكانيك الكم[ر]. ويكون فيه الاندفاع الزاوي (المداري) مكمَّى، ولا يأخذ كل الاتجاهات بالنسبة لاتجاه مؤثر محدَّد كالحقل المغنطيسي بل يأخذ اتجاهات محدّدة بمسقطه على هذا الاتجاه ويتحدد طوله بالعلاقة ومسقطه بـ hm[ر.الأعداد الكمومية]. حيث h ثابتة بلانك مقسومة بـ . كما يظهر في ميكانيك الكم اندفاع زاوي ذاتي (لف ذاتي) للإلكترون وللبروتون هو السبين S ويعامل معاملة الاندفاع الزاوي المداري. تبعاً لذلك تقدر العزوم المغنطيسية للإلكترونات بواحدة .

 العزم المغناطيسي

"Universal Resonance Curve", a symmetric approximation to the normalized response of a resonant circuit; abscissa values are deviation from center frequency, in units of center frequency divided by 2Q; ordinate is relative amplitude, and phase in cycles; dashed curves compare the range of responses of real two-pole circuits for a Q value of 5; for higher Q values, there is less deviation from the universal curve. Crosses mark the edges of the 3-dB bandwidth (gain 0.707, phase shift 45 degrees or 0.125 cycle).

أما العزوم المغنطيسية للنوى فتقدر بواحدة يستعاض فيها عن كتلة الإلكترون بكتلة البروتون الذي له شحنة مساوية بالقيمة لشحنة الإلكترون لكنها موجبة فتصبح قيمة الواحدة 5.05.10-27Am2 وتسمى مغنتون بور Bohr Magneton، وجميع العزوم مكمّاة. وتجمع عزوم مكوّنات جملة مدروسة جمعاً متجهاً لنحصل على العزم المغنطيسي الكلي . عندما توضع ذرة عزمها المغنطيسي ممثلاً بالشعاع في حقل مغنطيسي يبدأ هذا العزم بالمبادرة (الطواف) حول هذا الحقل بتواتر يسمى تواتر لارمور Larmor frequency WL معطى بالعلاقة: تعطى طاقة التفاعل بين الذرة والحقل المغنطيسي، إذا أخذنا اتجاه الحقل المغنطيسي هو اتجاه المحور oz بـ: حيث Sz مركبة السبين الذي يمكن أن يأخذ إحدى قيمتين

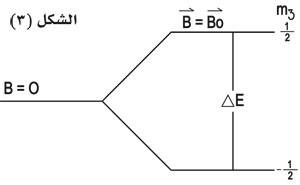
وعليه تنشطر السوية الواحدة قبل تطبيق الحقل، إلى سويتين الفرق بينهما هو ،

وسيكون التأثير أكثر تعقيداً عندما تكون الجملة ذات عزم مغنطيسي يختلف عن القيمة وتتعدد السويات تبعاً لذلك. وإذا قابلنا بين العلاقتين (3) و(4) نجد أن الانتقال من سوية الطاقة السفلى إلى السوية العليا يقابل تواتراً زاوياً هو تواتر لارمور wl. فإذا كانت جملة في السوية السفلى وامتصت طاقة من حقل مغنطيسي متناوب له هذا التواتر ستنتقل إلى السوية العليا، غير أن ظهور الأثر في الاتجاه العمودي يجعل ضرورة تطبيق هذا الحقل المتناوب بصورة عمودية على الحقل المغنطيسي الثابت B0 الذي جعل العزم المغنطيسي يُبادر. فإذا ما تمت مراقبة الطاقة التي يغذى بها الحقل المتناوب نجد عند تواتر لارمور امتصاصاً واضحاً لها. وقد أدت القياسات الدقيقة لتواترات التجاوب إلى التمييز بين ذرة في محيط أول عنه في محيط آخر متأثرة بالحقل المغنطيسي المحلّي الذي هو عبارة عن الحقل المغنطيسي المطبق مضافاً له تأثيرات الذرات أو العناصر المغنطيسية المجاورة المتمثلة بانزياح عن القيمة المقابلة لـ B0 تقع تواترات التجاوب من أجل تجاوب سبين الإلكترون في مجال الأمواج المكروية (غيغا هرتز 28 GHz~)[الأمواج الكهرومغنطيسية]. أما في حالة التجاوب المغنطيسي النووي والذي تمثله نوى الهدروجين فهو في مجال الأمواج الراديوية 42 MHz~، حين تكون قيمة الحقل المغنطيسي الثابت 1T (تسلا) أو 10K gauss.

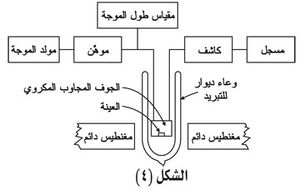
التجاوب المغنطيسي النووي للبروتونات (نوى الهدروجين) عند ثلاثة قيم للحقل المغنطيسي المعدَّل حيث تتغير قيمة الحقل ببطء حول قيمة ثابتة وتسمى القيمة المضافة حقل الكنس، والتي تقابل ثلاثة تواترات مختلفة بسبب اختلاف محيط كل منها على المستوى الذري، إذ يمكن لشرط التجاوب أن يتحقق وفق المعادلة (3) إما بتغيير التواتر أو بتغيير الحقل. فالتجاوب الأول يقابل الهدروجين في جزيئة الإيتانول عند الطرف الأيمن أما الثاني فيقابل المحيط CH2 والثالث يقابل المحيط OH. وإن هذه الاختلافات وإمكانية الفصل بينها هو الذي جعل من هذه التقنية مسباراً حيوياً. إضافة إلى مسألة عروض خطوط التجاوب وشدات التجاوب التي ظهرت هنا متناسبة مع عدد نوى الهدروجين المساهمة.

 استعراض

Resonance occurs when a system is able to store and easily transfer energy between two or more different storage modes (such as kinetic energy and potential energy in the case of a simple pendulum). However, there are some losses from cycle to cycle, called damping. When damping is small, the resonant frequency is approximately equal to the natural frequency of the system, which is a frequency of unforced vibrations. Some systems have multiple and distinct resonant frequencies.

 أمثلة

Pushing a person in a swing is a common example of resonance. The loaded swing, a pendulum, has a natural frequency of oscillation, its resonant frequency, and resists being pushed at a faster or slower rate.

A familiar example is a playground swing, which acts as a pendulum. Pushing a person in a swing in time with the natural interval of the swing (its resonant frequency) makes the swing go higher and higher (maximum amplitude), while attempts to push the swing at a faster or slower tempo produce smaller arcs.^:p.2–24 This is because the energy the swing absorbs is maximized when the pushes match the swing's natural oscillations.

Resonance occurs widely in nature, and is exploited in many devices. It is the mechanism by which virtually all sinusoidal waves and vibrations are generated. For example, when hard objects like metal, glass, or wood are struck, there are brief resonant vibrations in the object.^:p.2–24 Light and other short wavelength electromagnetic radiation is produced by resonance on an atomic scale, such as electrons in atoms. Other examples of resonance include:

• Timekeeping mechanisms of modern clocks and watches, e.g., the balance wheel in a mechanical watch and the quartz crystal in a quartz watch
• Tidal resonance of the Bay of Fundy
• Acoustic resonances of musical instruments and the human vocal tract
• Shattering of a crystal wineglass when exposed to a musical tone of the right pitch (its resonant frequency)
• Friction idiophones, such as making a glass object (glass, bottle, vase) vibrate by rubbing around its rim with a fingertip
• Electrical resonance of tuned circuits in radios and TVs that allow radio frequencies to be selectively received
• Creation of coherent light by optical resonance in a laser cavity
• Orbital resonance as exemplified by some moons of the Solar System's giant planets and resonant groups such as the plutinos
• Material resonances in atomic scale are the basis of several spectroscopic techniques that are used in condensed matter physics
  • Electron spin resonance
  • Mössbauer effect
  • Nuclear magnetic resonance

 الأنظمة الخطية

Resonance manifests itself in many linear and nonlinear systems as oscillations around an equilibrium point. When the system is driven by a sinusoidal external input, a measured output of the system may oscillate in response. The ratio of the amplitude of the output's steady-state oscillations to the input's oscillations is called the gain, and the gain can be a function of the frequency of the sinusoidal external input. Peaks in the gain at certain frequencies correspond to resonances, where the amplitude of the measured output's oscillations are disproportionately large.

Since many linear and nonlinear systems that oscillate are modeled as harmonic oscillators near their equilibria, a derivation of the resonant frequency for a driven, damped harmonic oscillator is shown. An RLC circuit is used to illustrate connections between resonance and a system's transfer function, frequency response, poles, and zeroes. Building off the RLC circuit example, these connections for higher-order linear systems with multiple inputs and outputs are generalized.

 The driven, damped harmonic oscillator

المقالة الرئيسية: Harmonic oscillator § Driven harmonic oscillators

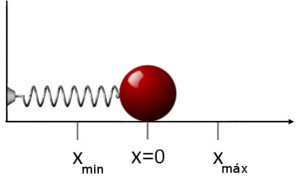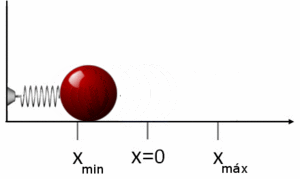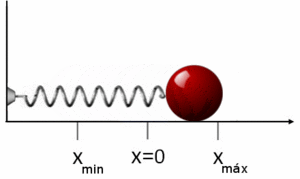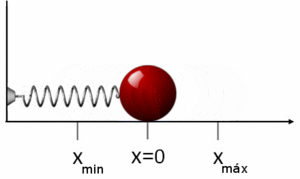
Consider a damped mass on a spring driven by a sinusoidal, externally applied force. Newton's second law takes the form

$$m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}},$$

(1)

where m is the mass, x is the displacement of the mass from the equilibrium point, F₀ is the driving amplitude, ω is the driving angular frequency, k is the spring constant, and c is the viscous damping coefficient. This can be rewritten in the form

$${\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\sin(\omega t),$$

(2)

where

• ${\textstyle \omega _{0}={\sqrt {k/m}}}$ is called the undamped angular frequency of the oscillator or the natural frequency,
• $\zeta ={\frac {c}{2{\sqrt {mk}}}}$ is called the damping ratio.

Many sources also refer to ω₀ as the resonant frequency. However, as shown below, when analyzing oscillations of the displacement x(t), the resonant frequency is close to but not the same as ω₀. In general the resonant frequency is close to but not necessarily the same as the natural frequency. The RLC circuit example in the next section gives examples of different resonant frequencies for the same system.

The general solution of Equation (2) is the sum of a transient solution that depends on initial conditions and a steady state solution that is independent of initial conditions and depends only on the driving amplitude F₀, driving frequency ω, undamped angular frequency ω₀, and the damping ratio ζ. The transient solution decays in a relatively short amount of time, so to study resonance it is sufficient to consider the steady state solution.

It is possible to write the steady-state solution for x(t) as a function proportional to the driving force with an induced phase change φ,

$$x(t)={\frac {F_{0}}{m{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}}\sin(\omega t+\varphi ),$$

(3)

where $\varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .$

The phase value is usually taken to be between −180° and 0 so it represents a phase lag for both positive and negative values of the arctan argument.

Steady-state variation of amplitude with relative frequency $\omega /\omega _{0}$ and damping $\zeta$ of a driven simple harmonic oscillator

Resonance occurs when, at certain driving frequencies, the steady-state amplitude of x(t) is large compared to its amplitude at other driving frequencies. For the mass on a spring, resonance corresponds physically to the mass's oscillations having large displacements from the spring's equilibrium position at certain driving frequencies. Looking at the amplitude of x(t) as a function of the driving frequency ω, the amplitude is maximal at the driving frequency

$$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.$$

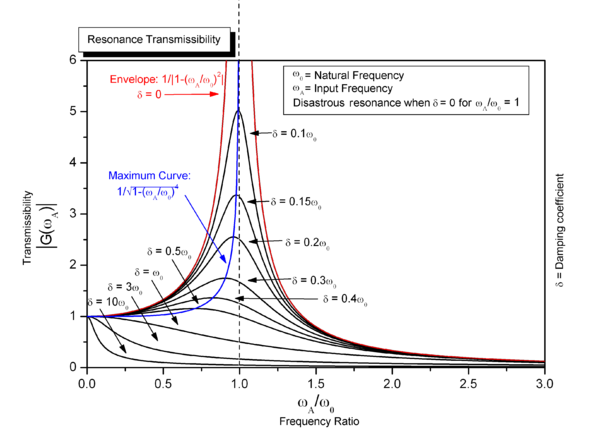
ω_r is the resonant frequency for this system. Again, the resonant frequency does not equal the undamped angular frequency ω₀ of the oscillator. They are proportional, and if the damping ratio goes to zero they are the same, but for non-zero damping they are not the same frequency. As shown in the figure, resonance may also occur at other frequencies near the resonant frequency, including ω₀, but the maximum response is at the resonant frequency.

Also, ω_r is only real and non-zero if ${\textstyle \zeta <1/{\sqrt {2}}}$, so this system can only resonate when the harmonic oscillator is significantly underdamped. For systems with a very small damping ratio and a driving frequency near the resonant frequency, the steady state oscillations can become very large.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 البندول

For other driven, damped harmonic oscillators whose equations of motion do not look exactly like the mass on a spring example, the resonant frequency remains

$$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}},$$

but the definitions of ω₀ and ζ change based on the physics of the system. For a pendulum of length ℓ and small displacement angle θ, Equation (1) becomes

$$m\ell {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-mg\theta -c\ell {\frac {\mathrm {d} \theta }{\mathrm {d} t}}$$

and therefore

• $\omega _{0}={\sqrt {\frac {g}{\ell }}},$
• $\zeta ={\frac {c}{2m}}{\sqrt {\frac {\ell }{g}}}.$

 RLC series circuits

انظر أيضاً: RLC Circuit § Series circuit

An RLC series circuit

Consider a circuit consisting of a resistor with resistance R, an inductor with inductance L, and a capacitor with capacitance C connected in series with current i(t) and driven by a voltage source with voltage v_in(t). The voltage drop around the circuit is

$L{\frac {di(t)}{dt}}+Ri(t)+V(0)+{\frac {1}{C}}\int _{0}^{t}i(\tau )d\tau =v_{\text{in}}(t).$

(4)

Rather than analyzing a candidate solution to this equation like in the mass on a spring example above, this section will analyze the frequency response of this circuit. Taking the Laplace transform of Equation (4),

$$sLI(s)+RI(s)+{\frac {1}{sC}}I(s)=V_{\text{in}}(s),$$

where I(s) and V_in(s) are the Laplace transform of the current and input voltage, respectively, and s is a complex frequency parameter in the Laplace domain. Rearranging terms,

$$I(s)={\frac {s}{s^{2}L+Rs+{\frac {1}{C}}}}V_{\text{in}}(s).$$

 Voltage across the capacitor

An RLC circuit in series presents several options for where to measure an output voltage. Suppose the output voltage of interest is the voltage drop across the capacitor. As shown above, in the Laplace domain this voltage is

$$V_{\text{out}}(s)={\frac {1}{sC}}I(s)$$

or

$$V_{\text{out}}={\frac {1}{LC(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{\text{in}}(s).$$

Define for this circuit a natural frequency and a damping ratio,

$$\omega _{0}={\frac {1}{\sqrt {LC}}},$$

$$\zeta ={\frac {R}{2}}{\sqrt {\frac {C}{L}}}.$$

The ratio of the output voltage to the input voltage becomes

$$H(s)\triangleq {\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}$$

H(s) is the transfer function between the input voltage and the output voltage. This transfer function has two poles–roots of the polynomial in the transfer function's denominator–at

$$s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}}$$

(5)

and no zeros–roots of the polynomial in the transfer function's numerator. Moreover, for ζ ≤ 1, the magnitude of these poles is the natural frequency ω₀ and that for ζ < 1/${\sqrt {2}}$, our condition for resonance in the harmonic oscillator example, the poles are closer to the imaginary axis than to the real axis.

Evaluating H(s) along the imaginary axis s = iω, the transfer function describes the frequency response of this circuit. Equivalently, the frequency response can be analyzed by taking the Fourier transform of Equation (4) instead of the Laplace transform. The transfer function, which is also complex, can be written as a gain and phase,

$$H(i\omega )=G(\omega )e^{i\Phi (\omega )}.$$

Bode magnitude plot for the voltage across the elements of an RLC series circuit. Natural frequency ω₀ = 1 rad/s, damping ratio ζ = 0.4. The capacitor voltage peaks below the circuit's natural frequency, the inductor voltage peaks above the natural frequency, and the resistor voltage peaks at the natural frequency with a peak gain of one. The gain for the voltage across the capacitor and inductor combined in series shows antiresonance, with gain going to zero at the natural frequency.

A sinusoidal input voltage at frequency ω results in an output voltage at the same frequency that has been scaled by G(ω) and has a phase shift Φ(ω). The gain and phase can be plotted versus frequency on a Bode plot. For the RLC circuit's capacitor voltage, the gain of the transfer function H(iω) is

$$G(\omega )={\frac {\omega _{0}^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

(6)

Note the similarity between the gain here and the amplitude in Equation (3). Once again, the gain is maximized at the resonant frequency

$$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.$$

Here, the resonance corresponds physically to having a relatively large amplitude for the steady state oscillations of the voltage across the capacitor compared to its amplitude at other driving frequencies.

 Voltage across the inductor

The resonant frequency need not always take the form given in the examples above. For the RLC circuit, suppose instead that the output voltage of interest is the voltage across the inductor. As shown above, in the Laplace domain the voltage across the inductor is

$$V_{\text{out}}(s)=sLI(s),$$

$$V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s),$$

$$V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}V_{\text{in}}(s),$$

using the same definitions for ω₀ and ζ as in the previous example. The transfer function between V_in(s) and this new V_out(s) across the inductor is

$$H(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$$

This transfer function has the same poles as the transfer function in the previous example, but it also has two zeroes in the numerator at s = 0. Evaluating H(s) along the imaginary axis, its gain becomes

$$G(\omega )={\frac {\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

Compared to the gain in Equation (6) using the capacitor voltage as the output, this gain has a factor of ω² in the numerator and will therefore have a different resonant frequency that maximizes the gain. That frequency is

$$\omega _{r}={\frac {\omega _{0}}{\sqrt {1-2\zeta ^{2}}}},$$

So for the same RLC circuit but with the voltage across the inductor as the output, the resonant frequency is now larger than the natural frequency, though it still tends towards the natural frequency as the damping ratio goes to zero. That the same circuit can have different resonant frequencies for different choices of output is not contradictory. As shown in Equation (4), the voltage drop across the circuit is divided among the three circuit elements, and each element has different dynamics. The capacitor's voltage grows slowly by integrating the current over time and is therefore more sensitive to lower frequencies, whereas the inductor's voltage grows when the current changes rapidly and is therefore more sensitive to higher frequencies. While the circuit as a whole has a natural frequency where it tends to oscillate, the different dynamics of each circuit element make each element resonate at a slightly different frequency.

 Voltage across the resistor

Suppose that the output voltage of interest is the voltage across the resistor. In the Laplace domain the voltage across the resistor is

$$V_{\text{out}}(s)=RI(s),$$

$$V_{\text{out}}(s)={\frac {Rs}{L\left(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}\right)}}V_{\text{in}}(s),$$

and using the same natural frequency and damping ratio as in the capacitor example the transfer function is

$$H(s)={\frac {2\zeta \omega _{0}s}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$$

This transfer function also has the same poles as the previous RLC circuit examples, but it only has one zero in the numerator at s = 0. For this transfer function, its gain is

$$G(\omega )={\frac {2\zeta \omega _{0}\omega }{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

The resonant frequency that maximizes this gain is

$$\omega _{r}=\omega _{0},$$

and the gain is one at this frequency, so the voltage across the resistor resonates at the circuit's natural frequency and at this frequency the amplitude of the voltage across the resistor equals the input voltage's amplitude.

 Antiresonance

المقالة الرئيسية: Antiresonance

Some systems exhibit antiresonance that can be analyzed in the same way as resonance. For antiresonance, the amplitude of the response of the system at certain frequencies is disproportionately small rather than being disproportionately large. In the RLC circuit example, this phenomenon can be observed by analyzing both the inductor and the capacitor combined.

Suppose that the output voltage of interest in the RLC circuit is the voltage across the inductor and the capacitor combined in series. Equation (4) showed that the sum of the voltages across the three circuit elements sums to the input voltage, so measuring the output voltage as the sum of the inductor and capacitor voltages combined is the same as v_in minus the voltage drop across the resistor. The previous example showed that at the natural frequency of the system, the amplitude of the voltage drop across the resistor equals the amplitude of v_in, and therefore the voltage across the inductor and capacitor combined has zero amplitude. We can show this with the transfer function.

The sum of the inductor and capacitor voltages is

$$V_{\text{out}}(s)=(sL+{\frac {1}{sC}})I(s),$$

$$V_{\text{out}}(s)={\frac {s^{2}+{\frac {1}{LC}}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s).$$

Using the same natural frequency and damping ratios as the previous examples, the transfer function is

$$H(s)={\frac {s^{2}+\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$$

This transfer has the same poles as the previous examples but has zeroes at

$$s=\pm i\omega _{0}.$$

(7)

Evaluating the transfer function along the imaginary axis, its gain is

$$G(\omega )={\frac {\omega _{0}^{2}-\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

Rather than look for resonance, i.e., peaks of the gain, notice that the gain goes to zero at ω = ω₀, which complements our analysis of the resistor's voltage. This is called antiresonance, which has the opposite effect of resonance. Rather than result in outputs that are disproportionately large at this frequency, this circuit with this choice of output has no response at all at this frequency. The frequency that is filtered out corresponds exactly to the zeroes of the transfer function, which were shown in Equation (7) and were on the imaginary axis.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Relationships between resonance and frequency response in the RLC series circuit example

These RLC circuit examples illustrate how resonance is related to the frequency response of the system. Specifically, these examples illustrate:

• How resonant frequencies can be found by looking for peaks in the gain of the transfer function between the input and output of the system, for example in a Bode magnitude plot
• How the resonant frequency for a single system can be different for different choices of system output
• The connection between the system's natural frequency, the system's damping ratio, and the system's resonant frequency
• The connection between the system's natural frequency and the magnitude of the transfer function's poles, pointed out in Equation (5), and therefore a connection between the poles and the resonant frequency
• A connection between the transfer function's zeroes and the shape of the gain as a function of frequency, and therefore a connection between the zeroes and the resonant frequency that maximizes gain
• A connection between the transfer function's zeroes and antiresonance

The next section extends these concepts to resonance in a general linear system.

 Generalizing resonance and antiresonance for linear systems

Next consider an arbitrary linear system with multiple inputs and outputs. For example, in state-space representation a third order linear time-invariant system with three inputs and two outputs might be written as

$${\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\end{bmatrix}}=A{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+B{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},$$

$${\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}=C{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+D{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},$$

where u_i(t) are the inputs, x_i(t) are the state variables, y_i(t) are the outputs, and A, B, C, and D are matrices describing the dynamics between the variables.

This system has a transfer function matrix whose elements are the transfer functions between the various inputs and outputs. For example,

$${\begin{bmatrix}Y_{1}(s)\\Y_{2}(s)\end{bmatrix}}={\begin{bmatrix}H_{11}(s)&H_{12}(s)&H_{13}(s)\\H_{21}(s)&H_{22}(s)&H_{23}(s)\end{bmatrix}}{\begin{bmatrix}U_{1}(s)\\U_{2}(s)\\U_{3}(s)\end{bmatrix}}.$$

Each H_ij(s) is a scalar transfer function linking one of the inputs to one of the outputs. The RLC circuit examples above had one input voltage and showed four possible output voltages–across the capacitor, across the inductor, across the resistor, and across the capacitor and inductor combined in series–each with its own transfer function. If the RLC circuit were set up to measure all four of these output voltages, that system would have a 4×1 transfer function matrix linking the single input to each of the four outputs.

Evaluated along the imaginary axis, each H_ij(iω) can be written as a gain and phase shift,

$$H_{ij}(i\omega )=G_{ij}(\omega )e^{i\Phi _{ij}(\omega )}.$$

Peaks in the gain at certain frequencies correspond to resonances between that transfer function's input and output, assuming the system is stable.

Each transfer function H_ij(s) can also be written as a fraction whose numerator and denominator are polynomials of s.

$$H_{ij}(s)={\frac {N_{ij}(s)}{D_{ij}(s)}}.$$

The complex roots of the numerator are called zeroes, and the complex roots of the denominator are called poles. For a stable system, the positions of these poles and zeroes on the complex plane give some indication of whether the system can resonate or antiresonate and at which frequencies. In particular, any stable or marginally stable, complex conjugate pair of poles with imaginary components can be written in terms of a natural frequency and a damping ratio as

$$s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}},$$

as in Equation (5). The natural frequency ω₀ of that pole is the magnitude of the position of the pole on the complex plane and the damping ratio of that pole determines how quickly that oscillation decays. In general,

• Complex conjugate pairs of poles near the imaginary axis correspond to a peak or resonance in the frequency response in the vicinity of the pole's natural frequency. If the pair of poles is on the imaginary axis, the gain is infinite at that frequency.
• Complex conjugate pairs of zeroes near the imaginary axis correspond to a notch or antiresonance in the frequency response in the vicinity of the zero's frequency, i.e., the frequency equal to the magnitude of the zero. If the pair of zeroes is on the imaginary axis, the gain is zero at that frequency.

In the RLC circuit example, the first generalization relating poles to resonance is observed in Equation (5). The second generalization relating zeroes to antiresonance is observed in Equation (7). In the examples of the harmonic oscillator, the RLC circuit capacitor voltage, and the RLC circuit inductor voltage, "poles near the imaginary axis" corresponds to the significantly underdamped condition ζ < 1/${\sqrt {2}}$.

 الموجات المستقرة

المقالة الرئيسية: موجة مستقرة

A mass on a spring has one natural frequency, as it has a single درجة حرية

A physical system can have as many natural frequencies as it has degrees of freedom and can resonate near each of those natural frequencies. A mass on a spring, which has one degree of freedom, has one natural frequency. A double pendulum, which has two degrees of freedom, can have two natural frequencies. As the number of coupled harmonic oscillators increases, the time it takes to transfer energy from one to the next becomes significant. Systems with very large numbers of degrees of freedom can be thought of as continuous rather than as having discrete oscillators.

Energy transfers from one oscillator to the next in the form of waves. For example, the string of a guitar or the surface of water in a bowl can be modeled as a continuum of small coupled oscillators and waves can travel along them. In many cases these systems have the potential to resonate at certain frequencies, forming standing waves with large-amplitude oscillations at fixed positions. Resonance in the form of standing waves underlies many familiar phenomena, such as the sound produced by musical instruments, electromagnetic cavities used in lasers and microwave ovens, and energy levels of atoms.

 موجات مستقرة على وتر

A standing wave (in black), created when two waves moving from left and right meet and superimpose

When a string of fixed length is driven at a particular frequency, a wave propagates along the string at the same frequency. The waves reflect off the ends of the string, and eventually a steady state is reached with waves traveling in both directions. The waveform is the superposition of the waves.

At certain frequencies, the steady state waveform does not appear to travel along the string. At fixed positions called nodes, the string is never displaced. Between the nodes the string oscillates and exactly halfway between the nodes–at positions called anti-nodes–the oscillations have their largest amplitude.

Standing waves in a string – the fundamental mode and the first 5 harmonics.

For a string of length $L$ with fixed ends, the displacement $y(x,t)$ of the string perpendicular to the $x$-axis at time $t$ is

$$y(x,t)=2y_{\text{max}}\sin(kx)\cos(2\pi ft),$$

حيث

• $y_{\text{max}}$ is the amplitude of the left- and right-traveling waves interfering to form the standing wave,
• $k$ is the wave number,
• $f$ is the frequency.

The frequencies that resonate and form standing waves relate to the length of the string as

$$f={\frac {nv}{2L}},$$

$$n=1,2,3,\dots$$

where $v$ is the speed of the wave and the integer $n$ denotes different modes or harmonics. The standing wave with n = 1 oscillates at the fundamental frequency and has a wavelength that is twice the length of the string. The possible modes of oscillation form a harmonic series.

 الرنين في الشبكات المعقدة

A generalization to complex networks of coupled harmonic oscillators shows that such systems have a finite number of natural resonant frequencies, related to the topological structure of the network itself. In particular, such frequencies result related to the eigenvalues of the network's Laplacian matrix. Let ${\bf {A}}$ be the adjacency matrix describing the topological structure of the network and ${\bf {L}}={\bf {K}}-{\bf {A}}$ the corresponding Laplacian matrix, where ${\bf {K}}={\rm {diag}}\,\{k_{i}\}$ is the diagonal matrix of the degrees of the network's nodes. Then, for a network of classical and identical harmonic oscillators, when a sinusoidal driving force $f(t)=F_{0}\sin \omega t$ is applied to a specific node, the global resonant frequencies of the network are given by $\omega _{i}={\sqrt {1+\mu _{i}}}$ where $\mu _{i}$ are the eigenvalues of the Laplacian ${\bf {L}}$.

 الأنواع

 الميكانيكي

المقالة الرئيسية: الرنين الميكانيكي and رنين الأوتار

School resonating mass experiment

Mechanical resonance is the tendency of a mechanical system to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration than it does at other frequencies. It may cause violent swaying motions and even catastrophic failure in improperly constructed structures including bridges, buildings, trains, and aircraft. When designing objects, engineers must ensure the mechanical resonance frequencies of the component parts do not match driving vibrational frequencies of motors or other oscillating parts, a phenomenon known as resonance disaster.

Avoiding resonance disasters is a major concern in every building, tower, and bridge construction project. As a countermeasure, shock mounts can be installed to absorb resonant frequencies and thus dissipate the absorbed energy. The Taipei 101 building relies on a 660-tonne pendulum (730-short-ton)—a tuned mass damper—to cancel resonance. Furthermore, the structure is designed to resonate at a frequency that does not typically occur. Buildings in seismic zones are often constructed to take into account the oscillating frequencies of expected ground motion. In addition, engineers designing objects having engines must ensure that the mechanical resonant frequencies of the component parts do not match driving vibrational frequencies of the motors or other strongly oscillating parts.

Clocks keep time by mechanical resonance in a balance wheel, pendulum, or quartz crystal.

The cadence of runners has been hypothesized to be energetically favorable due to resonance between the elastic energy stored in the lower limb and the mass of the runner.

 محطة الفضاء الدولية

The rocket engines for the International Space Station (ISS) are controlled by an autopilot. Ordinarily, uploaded parameters for controlling the engine control system for the Zvezda module make the rocket engines boost the International Space Station to a higher orbit. The rocket engines are hinge-mounted, and ordinarily the crew does not notice the operation. On January 14, 2009, however, the uploaded parameters made the autopilot swing the rocket engines in larger and larger oscillations, at a frequency of 0.5 Hz. These oscillations were captured on video, and lasted for 142 seconds.

 الصوتي

المقالة الرئيسية: الرنين الصوتي

Acoustic resonance is a branch of mechanical resonance that is concerned with the mechanical vibrations across the frequency range of human hearing, in other words sound. For humans, hearing is normally limited to frequencies between about 20 Hz and 20,000 Hz (20 kHz), Many objects and materials act as resonators with resonant frequencies within this range, and when struck vibrate mechanically, pushing on the surrounding air to create sound waves. This is the source of many percussive sounds we hear.

Acoustic resonance is an important consideration for instrument builders, as most acoustic instruments use resonators, such as the strings and body of a violin, the length of tube in a flute, and the shape of, and tension on, a drum membrane.

Like mechanical resonance, acoustic resonance can result in catastrophic failure of the object at resonance. The classic example of this is breaking a wine glass with sound at the precise resonant frequency of the glass, although this is difficult in practice.

 الكهربائي

المقالة الرئيسية: Electrical resonance

Animation illustrating electrical resonance in a tuned circuit, consisting of a capacitor (C) and an inductor (L) connected together. Charge flows back and forth between the capacitor plates through the inductor. Energy oscillates back and forth between the capacitor's electric field (E) and the inductor's magnetic field (B).

Electrical resonance occurs in an electric circuit at a particular resonant frequency when the impedance of the circuit is at a minimum in a series circuit or at maximum in a parallel circuit (usually when the transfer function peaks in absolute value). Resonance in circuits are used for both transmitting and receiving wireless communications such as television, cell phones and radio.

 البصري

المقالة الرئيسية: Optical cavity

An optical cavity, also called an optical resonator, is an arrangement of mirrors that forms a standing wave cavity resonator for light waves. Optical cavities are a major component of lasers, surrounding the gain medium and providing feedback of the laser light. They are also used in optical parametric oscillators and some interferometers. Light confined in the cavity reflects multiple times producing standing waves for certain resonant frequencies. The standing wave patterns produced are called "modes". Longitudinal modes differ only in frequency while transverse modes differ for different frequencies and have different intensity patterns across the cross-section of the beam. Ring resonators and whispering galleries are examples of optical resonators that do not form standing waves.

Different resonator types are distinguished by the focal lengths of the two mirrors and the distance between them; flat mirrors are not often used because of the difficulty of aligning them precisely. The geometry (resonator type) must be chosen so the beam remains stable, i.e., the beam size does not continue to grow with each reflection. Resonator types are also designed to meet other criteria such as minimum beam waist or having no focal point (and therefore intense light at that point) inside the cavity.

Optical cavities are designed to have a very large Q factor. A beam reflects a large number of times with little attenuation—therefore the frequency line width of the beam is small compared to the frequency of the laser.

Additional optical resonances are guided-mode resonances and surface plasmon resonance, which result in anomalous reflection and high evanescent fields at resonance. In this case, the resonant modes are guided modes of a waveguide or surface plasmon modes of a dielectric-metallic interface. These modes are usually excited by a subwavelength grating.

 المداري

المقالة الرئيسية: Orbital resonance

In celestial mechanics, an orbital resonance occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other, usually due to their orbital periods being related by a ratio of two small integers. Orbital resonances greatly enhance the mutual gravitational influence of the bodies. In most cases, this results in an unstable interaction, in which the bodies exchange momentum and shift orbits until the resonance no longer exists. Under some circumstances, a resonant system can be stable and self-correcting, so that the bodies remain in resonance. Examples are the 1:2:4 resonance of Jupiter's moons Ganymede, Europa, and Io, and the 2:3 resonance between Pluto and Neptune. Unstable resonances with Saturn's inner moons give rise to gaps in the rings of Saturn. The special case of 1:1 resonance (between bodies with similar orbital radii) causes large Solar System bodies to clear the neighborhood around their orbits by ejecting nearly everything else around them; this effect is used in the current definition of a planet.

 التصوير

21.2 T NMR Magnet at HWB-NMR, Birmingham, UK. In its strong field, the proton resonance is at 900MHz.

الوسائط الإضافية التي تسهم في التصوير بالتجاوب المغنطيسي النووي إلى جانب التواتر التجاوبي هي عرض التجاوب وسلوكه مع تغير الزمن. يرتبط عرض خط التجاوب الميكانيكي بالاحتكاك المفروض على الجملة وفي التجاوب الكهربائي[ر] بالمقاومة الكهربائية في الدارة. وكلما صغر الاحتكاك أو المقاومة صار التجاوب حاداً. وفي التجاوب المغنطيسي الذي يعمل على المستوى الذري يلعب تفاعل (تآثر) العزوم المغنطيسية بعضها مع بعض دور الاحتكاك، وتدرس هذه التفاعلات بدراسة سلوك العزوم المغنطيسية بعد قطع الحقل المغنطيسي العرضي (المتناوب) عنها. فتتميز عودتها إلى وضعها الأصلي بما يعرف زمن الاسترخاء relaxation times وله حالتان: زمن الاسترخاء الطولي T1 وزمن الاسترخاء العرضي T2. الأول مرتبط بتأثير اهتزازات الذرات أو شبكة الذرات phonons الفونونات على العزوم المغنطيسية، تفاعل السبين والشبكة spin-lattice، أما الثاني فمرتبط بتأثير العزوم المغنطيسية بعضها على بعض ويسمى زمن استرخاء السبين مع السبين spin-spin، وتعتمد شدة التمييز بين خطوط التجاوب المختلفة وطريقة أخذ العينات بالحاسوب لمعالجتها واستخلاص الصورة التجاوبية على هاتين الثابتتين الزمنيتين.

إن أهمية الاختلافات المحلّية المتعلقة بالتركيب الجزيئي التي يمكن كشفها بالتجاوب المغنطيسي ودقة هذا الكشف المقاربة لجزء من مئة مليون جزء جعل الكيميائيين يهتمون بالفروق بين الحقل المطبق B0 والحقل المقيس B ليعبّر عن الأثر المحلي بالإزاحة وسموها الانزياحات الكيميائية. وعند عدم معرفتنا الدقيقة بالحقل المحلّي يؤخذ سائل عياري متغير التراكيز ومعروف البنية الجزيئية وتقارن النتائج به لتعرفها. وتعد الآن خارطة الحقول المزاحة للبروتونات في كل الجذور الحرة المتوفرة ولدى فحص مادة غير معروفة تقارن المنحنيات الناتجة بالتجربة مع الخطوط الموجودة على الخارطة، ومن هذا يمكن معرفة الأوساط البروتونية الموجودة في المادة.

 التصوير بالرنين المغناطيسي

تعد تقنية التصوير بالتجاوب المغنطيسي إحدى الوسائل الفعالة في التشخيص السريري في الوقت الراهن، فلها ميّزة عدم إيذاء الأنسجة كما أنها، خلافاً لتقنية التصوير بأشعة x، لا تعرّض المريض إلى إشعاع مؤذٍ. وتعتمد طريقة التصوير على توزع الهدروجين في النسيج الذي يؤخذ كعامل تباين في هذه الطريقة.

للحصول على صورة بالتجاوب المغنطيسي يوضع المرضى المراد تصويرهم داخل حقل مغنطيسي ساكن ويحاطون بوشائع ذات تواتر راديوي متصلة بمستقبل وحاسوب. وأثناء عملية التصوير ترسل الوشائع إلى المريض سلسلة من نبضات راديوية قصيرة (مكرو ثانية) وتقوم الوشائع نفسها بتسجيل إشارات التجاوب المغنطيسي التي تستخدم فيما بعد لتشكيل الصورة.

وقد طورت أنواع مختلفة من الوشائع والنبضات لتلائم احتياجات طبية محدَّدة. وتتضمن الطريقة تطبيق نبضة مفردة راديوية لإثارة النوى، ثم يلي ذلك تطبيق نبضة ثانية مماثلة لتوليد «صدى سبيني»، وهذا الصدى السبيني يقدم معلومات قيمة حول الخصائص الفيزيائية للنسيج.

من الممكن إجراء تكويد مكافئ لإشارات التجاوب المغنطيسي التي تصدر عن أجزاء مختلفة من الجسم وذلك بتطبيق تدرج حقل مغنطيسي في كلا الاتجاهين الطولي والعرضي. ويعمل تدرج الحقل المغنطيسي على انتشار التواتر التجاوبي للنوى، بينما تستخدم تقنيات تحليل فورييه لتحليل الإشارات المتولدة عند كل تواتر. وهذا يجعل عملية بناء صورة في الفضاء ثلاثي البعد ممكناً. وتعكس الإشارة المغنطيسية التجاوبية عدداً من الوسطاء الفيزيائية، منها كثافة البروتونات وحركية الماء عند تلك النقطة. كما تدل على نوع النسيج لأن الوقت الذي تستغرقه السبينات كي تعود للاسترخاء في حالتها المألوفة يتوقف على نوع النسيج ويمكن الاستفادة من فترات الاسترخاء هذه للتمييز ما بين نسيج سليم وآخر معتل من الاختلاف بالإضاءة فيهما.

ولما كانت تقنية NMR التقليدية تعتمد على كشف الإشارات التي تولدها السبينات النووية للبروتونات الموجودة في الماء والدهن، فإن أحدث التجهيزات المتوفرة لم تستطع أن تصور مكنونات الرئة لأن كثافة البروتونات في نسيج الرئة منخفضة جداً لا تسمح بتوليد صورة واضحة. وقد أمكن حديثاً التغلب على هذه الصعوبة بإدخال غازات مفرطة الاستقطاب من الهليوم والكزينون حيث تتراصف فيها السبينات النووية مما يؤدي إلى تقوية الإشارة بحيث تصبح قادرة على تصوير الفراغات الهوائية المنتشرة في نسيج الرئة.

 العيوب

A column of soldiers marching in regular step on a narrow and structurally flexible bridge can set it into dangerously large amplitude oscillations. On April 12, 1831, the Broughton Suspension Bridge near Salford, England collapsed while a group of British soldiers were marching across. Since then, the British Army has had a standing order for soldiers to break stride when marching across bridges, to avoid resonance from their regular marching pattern affecting the bridge.

Vibrations of a motor or engine can induce resonant vibration in its supporting structures if their natural frequency is close to that of the vibrations of the engine. A common example is the rattling sound of a bus body when the engine is left idling.

Structural resonance of a suspension bridge induced by winds can lead to its catastrophic collapse. Several early suspension bridges in Europe and United States were destroyed by structural resonance induced by modest winds. The collapse of the Tacoma Narrows Bridge on 7 November 1940 is characterized in physics as a classic example of resonance. It has been argued by Robert H. Scanlan and others that the destruction was instead caused by aeroelastic flutter, a complicated interaction between the bridge and the winds passing through it—an example of a self oscillation, or a kind of "self-sustaining vibration" as referred to in the nonlinear theory of vibrations.

 Q factor

المقالة الرئيسية: Q factor

High and low Q factor

The Q factor or quality factor is a dimensionless parameter that describes how under-damped an oscillator or resonator is, and characterizes the bandwidth of a resonator relative to its center frequency. A high value for Q indicates a lower rate of energy loss relative to the stored energy, i.e., the system is lightly damped. The parameter is defined by the equation:

$$Q=2\pi {\text{ }}{\frac {\text{ maximum energy stored}}{\text{total energy lost per cycle at resonance}}}$$

.

The higher the Q factor, the greater the amplitude at the resonant frequency, and the smaller the bandwidth, or range of frequencies around resonance occurs. In electrical resonance, a high-Q circuit in a radio receiver is more difficult to tune, but has greater selectivity, and so would be better at filtering out signals from other stations. High Q oscillators are more stable.

Examples that normally have a low Q factor include door closers (Q=0.5). Systems with high Q factors include tuning forks (Q=1000), atomic clocks and lasers (Q≈10¹¹).

 منحنى الرنين الشامل

"Universal Resonance Curve", a symmetric approximation to the normalized response of a resonant circuit; abscissa values are deviation from center frequency, in units of center frequency divided by 2Q; ordinate is relative amplitude, and phase in cycles; dashed curves compare the range of responses of real two-pole circuits for a Q value of 5; for higher Q values, there is less deviation from the universal curve. Crosses mark the edges of the 3 dB bandwidth (gain 0.707, phase shift 45° or 0.125 cycle).

The exact response of a resonance, especially for frequencies far from the resonant frequency, depends on the details of the physical system, and is usually not exactly symmetric about the resonant frequency, as illustrated for the simple harmonic oscillator above.

For a lightly damped linear oscillator with a resonance frequency $\omega _{0}$, the intensity of oscillations $I$ when the system is driven with a driving frequency $\omega$ is typically approximated by the following formula that is symmetric about the resonance frequency:

$$I(\omega )\equiv |\chi |^{2}\propto {\frac {1}{(\omega -\omega _{0})^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}.$$

Where the susceptibility $\chi (\omega )$ links the amplitude of the oscillator to the driving force in frequency space:

$$x(\omega )=\chi (\omega )F(\omega )$$

The intensity is defined as the square of the amplitude of the oscillations. This is a Lorentzian function, or Cauchy distribution, and this response is found in many physical situations involving resonant systems. Γ is a parameter dependent on the damping of the oscillator, and is known as the linewidth of the resonance. Heavily damped oscillators tend to have broad linewidths, and respond to a wider range of driving frequencies around the resonant frequency. The linewidth is inversely proportional to the Q factor, which is a measure of the sharpness of the resonance.

In radio engineering and electronics engineering, this approximate symmetric response is known as the universal resonance curve, a concept introduced by Frederick E. Terman in 1932 to simplify the approximate analysis of radio circuits with a range of center frequencies and Q values.

 انظر أيضا

	بوابة إلكترونيات
	بوابة فيزياء

• Cymatics
• Driven harmonic motion
• هندسة الزلازل
• Electric dipole spin resonance
• Formant
• Limbic resonance
• رنين غير خطي
• Normal mode
• Positive feedback
• رنين شومان
• Simple harmonic motion
• Stochastic resonance
• Sympathetic string
• رنين (كيمياء)
• رنين فرمي
• رنين (فيزياء الجسيمات)

 المصادر

محمد قعقع. "التجاوب المغنطيسي". الموسوعة العربية.

 المراجع

• Aspelmeyer, M; Kippenberg, Tobias J.; Marquardt, Florian (30 December 2014). "Cavity optomechanics". Reviews of Modern Physics. 86 (4): 1391. arXiv:1303.0733. Bibcode:2014RvMP...86.1391A. doi:10.1103/RevModPhys.86.1391. hdl:11858/00-001M-0000-002D-6464-3. S2CID 119252645.
• Billah, K. Yusuf; Scanlan, Robert H (1991). "Resonance, Tacoma Narrows Bridge Failure, and Undergraduate Physics Textbooks" (PDF). American Journal of Physics. 59 (2): 118–124. Bibcode:1991AmJPh..59..118B. doi:10.1119/1.16590. Archived (PDF) from the original on 2000-09-19. Retrieved 1 January 2021.
• Ghatak, Ajoy (2005). Optics (3rd ed.). New Delhi: Tata McGraw-Hill. ISBN 978-0-07-058583-6.
• Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentals of Physics. Vol. part 2 (7th ed.). John Wiley & Sons Ltd. ISBN 978-0-471-71716-4.
• Hardt, David (2004). "Understanding Poles and Zeros" (PDF). 2.14 Analysis and Design of Feedback Control Systems. Massachusetts Institute of Technology. Archived (PDF) from the original on 2022-10-09. Retrieved 18 April 2020.
• Harlow, James H., ed. (2004). Electric Power Transformer Engineering. London: CRC Press. ISBN 978-0-8493-1704-0.
• Ogata, Katsuhiko (2005). System Dynamics (4th ed.). Harlow: Pearson. ISBN 978-1-292-02608-4.
• Olson, Harry F. (1967). Music, Physics and Engineering. Vol. 2. New York: Dover Publications. ISBN 978-0-486-21769-7.
• Serway, Raymond A.; Faughn, Jerry S. (1992). College Physics (3rd ed.). Saunders College Publishing. ISBN 0-03-076377-0.
• Siebert, William McC. (1986). Circuits, Signals, and Systems. London; New York: MIT Press' McGraw Hill Book Company. ISBN 978-0-262-19229-3.
• Siegman, A. E. (1986). Lasers. University Science Books. ISBN 978-0-935702-11-8.
• Snyder, Kristine L.; Farley, Claire T. (2011). "Energetically optimal stride frequency in running: the effects of incline and decline". The Journal of Experimental Biology. 214 (12): 2089–2095. doi:10.1242/jeb.053157. PMID 21613526.
• Terman, Frederick Emmons (1932). Radio Engineering (1st ed.). New York: McGraw-Hill Book Company. OCLC 1036819790.
• Tooley, Michael H. (2006). Electronic Circuits: Fundamentals and Applications. Oxford: Taylor & Francis. ISBN 978-0-7506-6923-8.

 وصلات خارجية

• The Feynman Lectures on Physics Vol. I Ch. 23: Resonance
• Resonance Archived 2017-01-03 at the Wayback Machine - a chapter from an online textbook
• Greene, Brian, "Resonance in strings". The Elegant Universe, NOVA (PBS)
• Hyperphysics section on resonance concepts
• Resonance versus resonant (usage of terms)
• Wood and Air Resonance in a Harpsichord
• Breaking glass with sound Archived 2008-12-02 at the Wayback Machine, including high-speed footage of glass breaking