تذبذب (فيزياء)

لمعلومات عن الاستخدامات الأخرى، انظر تذبذب (كيمياء) وتذبذب.

"Oscillator" redirects here. For other uses, see Oscillator (توضيح).

"Vibrating" redirects here. For other uses, see Vibrations (disambiguation) and Vibrate (disambiguation).

An undamped spring–mass system is an oscillatory system

An undamped trifilar pendulum

التذبذب أو الذبذبة Oscillation، هو حركة تأرجحية لجسم جيئةً وذهاباً. تتذبذب جميع الأشياء ولكن بدرجات متفاوتة. ومن الممكن أن تكون الذبذبات ضعيفة جدًا أو سريعة جدًا أو بطيئة جدًا لحد يصعب كشفه. تحدث الذبذبة عند وقوع الزلازل وذلك بسبب تذبذب الجسيمات الصغيرة في باطن الأرض. كما تتولد الذبذبات عند تحرك أمواج البحر علوًّا وانخفاضًا مسببة المد والجزر. وتتذبذب السيارة نتيجة للانفجارات المتكررة في أسطوانات محركاتها. وتنتج الكثير من الأصوات نتيجة لذبذبة الأجسام.

تُستغل الذبذبات في الكثير من الأعمال النافعة. فعندما ننقر نقرة خفيفة على المملحة (الملاحة)، وهي وعاء صغير يوضع فيه الملح على مائدة الطعام، فإن الذبذبات التي تولدها هذه النقرة الخفيفة هي التي تجعل الملح يتحرك. ويستعمل عمال الطرق أجهزة معينة لتوليد الذبذبات التي تدك التربة التي تقام عليها الطُّرُق. وفي الطب تستعمل الذبذبات لعلاج أوجاع العضلات.

في الوقت ذاته من الممكن أن تجلب الذبذبات كثيرًا من المتاعب للبشر والآلات. فإذا تجاوز معدل الذبذبات وشدتها حدًا معينًا، على سبيل المثال، فإنها تتسبب في كثير من الإزعاج للناس. كما تؤدي ذبذبات الضوضاء، والذبذبات الكثيرة جدًا إلى فقدان البشر القدرة على التركيز وتولد لديهم الشعور بالمرض. أما بالنسبة للآلات فإن الذبذبات القوية فيها قد تتسبب في إحداث الضجيج وتصيبها بالتآكل والكسر.

ابتكر المهندسون عدة طرق للتخلص من مشاكل الذبذبات والاهتزازات. فقد استعان المهندسون بالمواد المرنة والزنبركات لتقليل تأثير الذبذبات والاهتزازات. على سبيل المثال، تم تزويد العربات بإطارات غازية (إطارات تنفخ بالهواء المضغوط) تمكنها من امتصاص الاهتزازات الناتجة من السفر فوق طرقات غير معبدة. ويتم تركيب مراوح التهوية في المباني على زنبركات فولاذية لينة. والواقع أن المهندسين يحاولون عموماً التخلص من مشاكل الذبذبات عند تصميمهم لأية آلة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الوصف

توصف الذبذبات بناءً على الاتساع أو التردد. والاتساع هو المسافة التي يقطعها جسم متذبذب من نقطة سكونه. أما التردد فهو عدد الذبذبات الكاملة التي يقطعها الجسم أثناء فترة زمنية محددة، عادة ثانية واحدة. ويقاس التردد بوحدة تُسمى هرتز. ويسمع معظم الناس الذبذبات عندما يتراوح مقدار ترددها بين 20 و 20,000 هرتز.

 التصنيف

ويمكن تصنيف الذبذبات إلى ذبذبات حرة وذبذبات قسرية. وفكرة هذا التصنيف قائمة على أساس هل القوة الخارجية هي التي تُبقِي استمرارية الذبذبات أم لا؟ فعلى سبيل المثال، يهتز وتر الجيتار بحرِّيَّة عند نقره، ولكن ذبذبة وتر الكمان تكون قسرية عندما يمرر القوس فوق الوتر. وتعتمد معظم آلات الموسيقى في علو أصواتها على ظاهرة تسمى الرنين. يحدث الرنين عندما تكون القوة المولّدة للذبذبة في تناغم مع تردد تذبذب الجسم الحر.

 الذبذبة التوافقية البسيطة

المقالة الرئيسية: الحركة التوافقية البسيطة

Simple harmonic motion.

ندرس هنا بغرض التوضيح الذبذبة التوافقية نظرا لأهميتها :

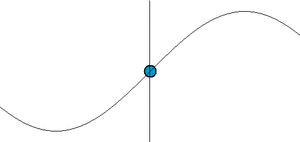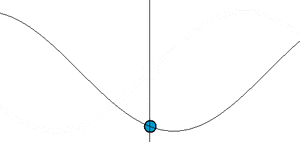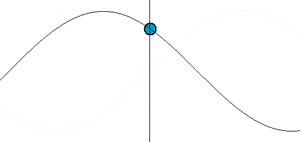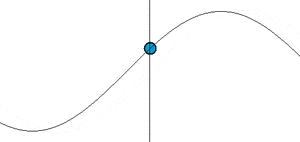
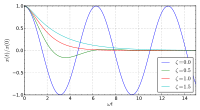
ويبين الرسم البياني ذبذبة توافقية ذات إزاحة

$y(t)$ للمطال $y_{0}$ والدورة $T$.

وتعطي القيمة $y(t)$ مقدار الإزاحة عند الزمن $t$ ، ويعطي المطال Amplitude القيمة العظمى للإزاحة . والدورة T هي الزمن الذي يتم فيه البندول ذبذبة كاملة ويصل بعدها إلى نفس نقطة البداية.

يسمى معكوس زمن الدورة f التردد.

أي أن:

$f={1 \over T}\quad$.

كما يوجد رمز آخر للتردد $\nu$ ويقاس بوحدة بالهرتز .

 Two-dimensional oscillators

In two or three dimensions, harmonic oscillators behave similarly to one dimension. The simplest example of this is an isotropic oscillator, where the restoring force is proportional to the displacement from equilibrium with the same restorative constant in all directions.

$${\vec {F}}=-k{\vec {r}}$$

This produces a similar solution, but now there is a different equation for every direction.

$${\begin{aligned}x(t)&=A_{x}\cos(\omega t-\delta _{x}),\\y(t)&=A_{y}\cos(\omega t-\delta _{y}),\\&\;\,\vdots \end{aligned}}$$

 Anisotropic oscillators

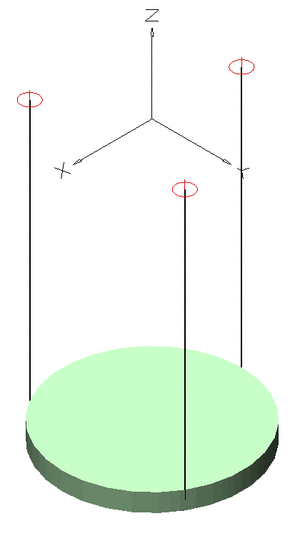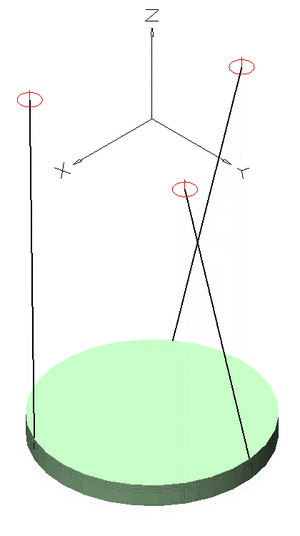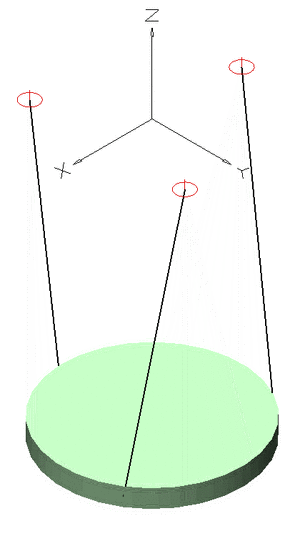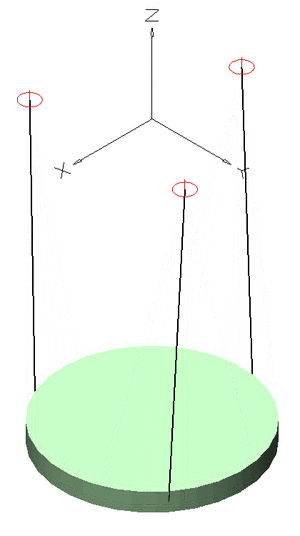
With anisotropic oscillators, different directions have different constants of restoring forces. The solution is similar to isotropic oscillators, but there is a different frequency in each direction. Varying the frequencies relative to each other can produce interesting results. For example, if the frequency in one direction is twice that of another, a figure eight pattern is produced. If the ratio of frequencies is irrational, the motion is quasiperiodic. This motion is periodic on each axis, but is not periodic with respect to r, and will never repeat.

 الذبذبة التوافقية المخمدة

المقالة الرئيسية: إخماد

اعتماد سلوك النظام على قيمة نسبة الإخماد ζ

توصف الحركة المذبذبة بأنها ذبذبة توافقية إذا كانت القوة المتحكمة في النظام متناسبة تناسبا طرديا مع الإزاحة . وتسمى هذه الحالة أيضا في الرياضيات بالنظام الخطي ، حيث تتغير القوة خطيا مع الإزاحة . أي إذا تضاعفت القوة تضاعفت الإزاحة وهكذا.

ويمكن وصف تلك الحركة التوافقية بالمعادلة :

$y(t)=y_{0}\cdot \sin(2\pi ft+\varphi _{0})\,$

حيث:

$y_{0}$  = المطال

$\varphi _{0}$  = الطور عند الزمن = 0.

حيث يسمى:

$\varphi (t)=2\pi ft+\varphi _{0}\,$

الطور الكلي ، كما يسمى :

f أو $\nu$ التردد .

ويسمي حاصل ضرب التردد في $2\pi$ ,

التردد الزاوي = $2\pi$ . f

للحركة. وبإدخال تعبير التردد الزاوي يمكن اختصار المعادلات :

$y(t)=y_{0}\cdot \sin(\omega \,t+\varphi _{0})\,$

فإذا فاضلنا المعادلة بالنسبة للزمن نحصل على:

$v(t)=\omega \cdot y_{0}\cdot \cos(\omega \,t+\varphi _{0})\,$

حيث:

$v(t)$ = سرعة الجسم المتذبذب .

وبإجراء التفاضل مرة ثانية :

$a(t)=-\omega ^{2}\cdot y_{0}\cdot \sin(\omega \,t+\varphi _{0})\,$

حيث:

$a(t)$ = عجلة الجسم المتذبذب.

 التذبذب المدفوع

In addition, an oscillating system may be subject to some external force, as when an AC circuit is connected to an outside power source. In this case the oscillation is said to be driven.

The simplest example of this is a spring-mass system with a sinusoidal driving force.

$${\ddot {x}}+2\beta {\dot {x}}+\omega _{0}^{2}x=f(t),$$

where $f(t)=f_{0}\cos(\omega t+\delta ).$

This gives the solution:

$$x(t)=A\cos(\omega t-\delta )+A_{tr}\cos(\omega _{1}t-\delta _{tr}),$$

where $A={\sqrt {\frac {f_{0}^{2}}{(\omega _{0}^{2}-\omega ^{2})+2\beta \omega }}}$ and $\delta =\tan ^{-1}\left({\frac {2\beta \omega }{\omega _{0}^{2}-\omega ^{2}}}\right)$

The second term of x(t) is the transient solution to the differential equation. The transient solution can be found by using the initial conditions of the system.

Some systems can be excited by energy transfer from the environment. This transfer typically occurs where systems are embedded in some fluid flow. For example, the phenomenon of flutter in aerodynamics occurs when an arbitrarily small displacement of an aircraft wing (from its equilibrium) results in an increase in the angle of attack of the wing on the air flow and a consequential increase in lift coefficient, leading to a still greater displacement. At sufficiently large displacements, the stiffness of the wing dominates to provide the restoring force that enables an oscillation.

 الرنين

Resonance occurs in a damped driven oscillator when ω = ω₀, that is, when the driving frequency is equal to the natural frequency of the system. When this occurs, the denominator of the amplitude is minimized, which maximizes the amplitude of the oscillations.

 التذبذب المعشق

Two pendulums with the same period fixed on a string act as pair of coupled oscillators. The oscillation alternates between the two.

المقالة الرئيسية: Injection locking

Experimental Setup of Huygens synchronization of two clocks

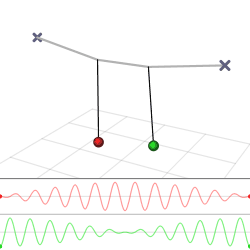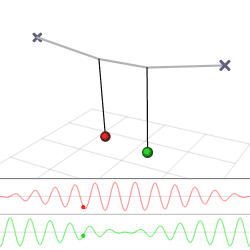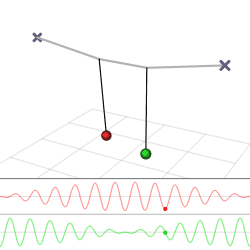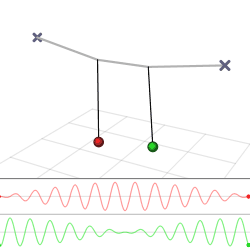
The harmonic oscillator and the systems it models have a single degree of freedom. More complicated systems have more degrees of freedom, for example, two masses and three springs (each mass being attached to fixed points and to each other). In such cases, the behavior of each variable influences that of the others. This leads to a coupling of the oscillations of the individual degrees of freedom. For example, two pendulum clocks (of identical frequency) mounted on a common wall will tend to synchronise. This phenomenon was first observed by Christiaan Huygens in 1665. The apparent motions of the compound oscillations typically appears very complicated but a more economic, computationally simpler and conceptually deeper description is given by resolving the motion into normal modes.

The simplest form of coupled oscillators is a 3 spring, 2 mass system, where masses and spring constants are the same. This problem begins with deriving Newton's second law for both masses.

$${\begin{cases}m_{1}{\ddot {x}}_{1}=-(k_{1}+k_{2})x_{1}+k_{2}x_{2}\\m_{2}{\ddot {x}}_{2}=k_{2}x_{1}-(k_{2}+k_{3})x_{2}\end{cases}}$$

The equations are then generalized into matrix form.

$$F=M{\ddot {x}}=kx,$$

where $M={\begin{bmatrix}m_{1}&0\\0&m_{2}\end{bmatrix}}$, $x={\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}$, and $k={\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\end{bmatrix}}$

The values of k and m can be substituted into the matrices.

$${\begin{aligned}m_{1}=m_{2}=m,\;\;k_{1}=k_{2}=k_{3}=k,\\M={\begin{bmatrix}m&0\\0&m\end{bmatrix}},\;\;k={\begin{bmatrix}2k&-k\\-k&2k\end{bmatrix}}\end{aligned}}$$

These matrices can now be plugged into the general solution.

$${\begin{aligned}\left(k-M\omega ^{2}\right)a&=0\\{\begin{bmatrix}2k-m\omega ^{2}&-k\\-k&2k-m\omega ^{2}\end{bmatrix}}&=0\end{aligned}}$$

The determinant of this matrix yields a quadratic equation.

$${\begin{aligned}&\left(3k-m\omega ^{2}\right)\left(k-m\omega ^{2}\right)=0\\&\omega _{1}={\sqrt {\frac {k}{m}}},\;\;\omega _{2}={\sqrt {\frac {3k}{m}}}\end{aligned}}$$

Depending on the starting point of the masses, this system has 2 possible frequencies (or a combination of the two). If the masses are started with their displacements in the same direction, the frequency is that of a single mass system, because the middle spring is never extended. If the two masses are started in opposite directions, the second, faster frequency is the frequency of the system.

More special cases are the coupled oscillators where energy alternates between two forms of oscillation. Well-known is the Wilberforce pendulum, where the oscillation alternates between the elongation of a vertical spring and the rotation of an object at the end of that spring.

Coupled oscillators are a common description of two related, but different phenomena. One case is where both oscillations affect each other mutually, which usually leads to the occurrence of a single, entrained oscillation state, where both oscillate with a compromise frequency. Another case is where one external oscillation affects an internal oscillation, but is not affected by this. In this case the regions of synchronization, known as Arnold Tongues, can lead to highly complex phenomena as for instance chaotic dynamics.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تقريب التذبذب الصغير

In physics, a system with a set of conservative forces and an equilibrium point can be approximated as a harmonic oscillator near equilibrium. An example of this is the Lennard-Jones potential, where the potential is given by:

$$U(r)=U_{0}\left[\left({\frac {r_{0}}{r}}\right)^{12}-\left({\frac {r_{0}}{r}}\right)^{6}\right]$$

The equilibrium points of the function are then found:

$${\begin{aligned}{\frac {dU}{dr}}&=0=U_{0}\left[-12r_{0}^{12}r^{-13}+6r_{0}^{6}r^{-7}\right]\\\Rightarrow r&\approx r_{0}\end{aligned}}$$

The second derivative is then found, and used to be the effective potential constant:

$${\begin{aligned}\gamma _{\text{eff}}&=\left.{\frac {d^{2}U}{dr^{2}}}\right|_{r=r_{0}}=U_{0}\left[12(13)r_{0}^{12}r^{-14}-6(7)r_{0}^{6}r^{-8}\right]\\[1ex]&={\frac {114U_{0}}{r^{2}}}\end{aligned}}$$

The system will undergo oscillations near the equilibrium point. The force that creates these oscillations is derived from the effective potential constant above:

$$F=-\gamma _{\text{eff}}(r-r_{0})=m_{\text{eff}}{\ddot {r}}$$

This differential equation can be re-written in the form of a simple harmonic oscillator:

$${\ddot {r}}+{\frac {\gamma _{\text{eff}}}{m_{\text{eff}}}}(r-r_{0})=0$$

Thus, the frequency of small oscillations is:

$$\omega _{0}={\sqrt {\frac {\gamma _{\text{eff}}}{m_{\text{eff}}}}}={\sqrt {\frac {114U_{0}}{r^{2}m_{\text{eff}}}}}$$

Or, in general form

$$\omega _{0}={\sqrt {\left.{\frac {d^{2}U}{dr^{2}}}\right\vert _{r=r_{0}}}}$$

This approximation can be better understood by looking at the potential curve of the system. By thinking of the potential curve as a hill, in which, if one placed a ball anywhere on the curve, the ball would roll down with the slope of the potential curve. This is true due to the relationship between potential energy and force.

$${\frac {dU}{dt}}=-F(r)$$

By thinking of the potential in this way, one will see that at any local minimum there is a "well" in which the ball would roll back and forth (oscillate) between $r_{\text{min}}$ and $r_{\text{max}}$. This approximation is also useful for thinking of Kepler orbits.

 الأنظمة-الموجات المستمرة

المقالة الرئيسية: Wave

As the number of degrees of freedom becomes arbitrarily large, a system approaches continuity; examples include a string or the surface of a body of water. Such systems have (in the classical limit) an infinite number of normal modes and their oscillations occur in the form of waves that can characteristically propagate.

 الرياضيات

المقالة الرئيسية: Oscillation (mathematics)

Oscillation of a sequence (shown in blue) is the difference between the limit superior and limit inferior of the sequence.

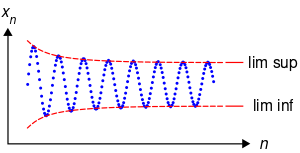
The mathematics of oscillation deals with the quantification of the amount that a sequence or function tends to move between extremes. There are several related notions: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval (or open set).

 أمثلة

ميكانيكي بندول مزدوج بندول فوكو رنان هلمهولتس Oscillations in the Sun (helioseismology)، النجوم (سايزمولوجيا النجوم) و تذبذبات النيوترون-نجم. Quantum harmonic oscillator Playground swing String instruments اهتزاز إلتوائي Tuning fork وتر مهتز بندول ولبرفورس Lever escapement  كهربائي  مقالة مفصلة: اهتزاز كهربائي  مقالة مفصلة: مذبذب إلكتروني تيار متناوب Armstrong (or Tickler or Meissner) oscillator Astable multivibrator Blocking oscillator Butler oscillator Clapp oscillator Colpitts oscillator Delay line oscillator Dow (or ultra-audion) oscillator Electronic oscillator Hartley oscillator Oscillistor Pierce oscillator Relaxation oscillator RLC circuit Royer oscillator Vačkář oscillator Wien bridge oscillator

إليكتروني-ميكانيكي Crystal oscillator مكبر صوت ميكروفون  بصري ليزر (تذبذب مجال كهرومغناطيسي بتردد of order 1015 Hz) Oscillator Toda or self-pulsation (pulsation of output power of laser at frequencies 104 Hz - 106 Hz in the transient regime) متذبذب كمومي قد يشير إلى متذبذب محلي بصري، وكذلك إلى نموذج معتاد في بصريات الكم.  حيوي Circadian rhythm Circadian oscillator معادلة لوتكا-ڤولترّا Lotka–Volterra تذبذب عصبي جين متذبذب  بشري تذبذب عصبي Insulin release oscillations gonadotropin releasing hormone pulsations Pilot-induced oscillation Voice production

اقتصادي واجتماعي دورة العمل فجوة أجيال Generation gap الاقتصاد المالتوسي News cycle  مناخي وجيوفيزيائي Atlantic multidecadal oscillation Chandler wobble El Niño-Southern Oscillation Pacific decadal oscillation Quasi-biennial oscillation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  فيزياء فلكية Neutron stars النموذج الدوري Cyclic Model  كيميائي Belousov–Zhabotinsky reaction Mercury beating heart تفاعل بريگز-راوشر Bray–Liebhafsky reaction

 انظر أيضا

Beat (acoustics) BIBO stability Critical speed دورة (موسيقى) Dynamical system هندسة الزلازل تغذية راجعة تذبذب (رياضيات)

Oscillator phase noise Periodic function Phase noise Reciprocating motion Resonator إيقاع Seasonality Self-exciting oscillation

تذبذب ذاتي Signal generator Strange attractor Structural stability Time period Tuned mass damper اهتزاز Vibrator (mechanical)

 وصلات خارجية

• Vibrations - a chapter from an online textbook