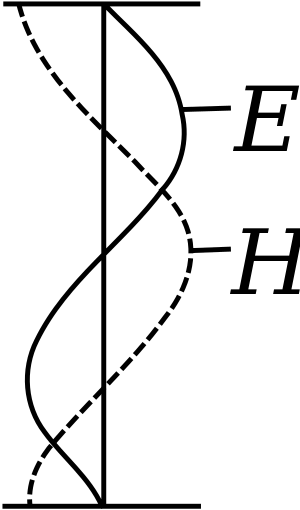
موجة مستقرة

موجات كهرومغناطيسية مستقرة في resonator. Waves at the top have larger frequencies than those below and are shifted upward for clarity. At both boundaries the walls require nodes in the waves, so only waves with multiple half-wavelengths λ/2 fit in the box: λ/2 = W, λ = W, 3λ/2 = W where W = width of cavity.

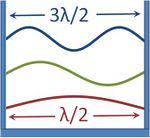
الموجة المستقرة standing wave، وتعرف أيضاً باسم الموجة الراكدة أو الموجة الواقفة stationary wave، هي موجة تظل في مكان ثابت. ويمكن لهذه الظاهرة أن تحدث إما لأن الوسط يتحرك في الاتجاه المعاكس للموجة، أو تحدث في وسط ساكن نتيجة تداخل بين موجتين تتحركان في اتجاهين متضادين. في الحالة الأخيرة، لموجات ذات سعة متساوية وتتحركان في اتجاهين مضادين، هناك في المتوسط صافي انتشار الطاقة الصافي مساوياً لصفر.

الموجات المستقرة في resonators هم أحد الأسباب للظاهرة المسماة رنين.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الوسط الذي تتم فيه الحركة

وكمثال للنوع الأول، في بعض ظروف الأرصاد الجوية تتشكل الموجات الراكدة في الغلاف الجوي في خلف سلاسل الجبال. ومثل هذه الموجات يستغلها طيارو الانزلاق الجوي.

الموجات الراكدة و hydraulic jumps يتشكلوا أيضاً في الأنهار سريعة الجريان وتيارات المد مثل سالتشتراومن مالستروم.

 الموجات المتضادة

موجة راكدة في وسط راكد. النقاط الحمراء تمثل نقاط الموجة.

A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue).

Electric force vector (E) and magnetic force vector (H) of a standing wave.

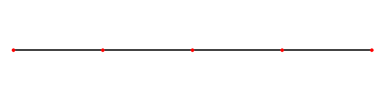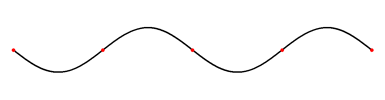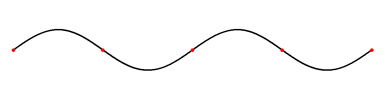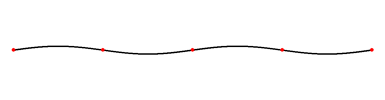
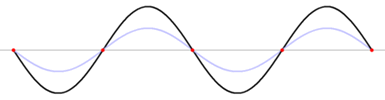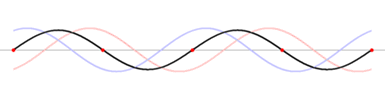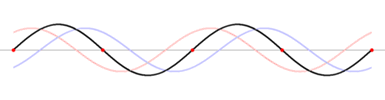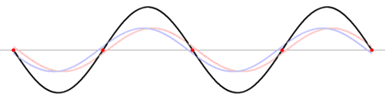
تحدث الموجات المستقرة stationary waves كلما التقت موجتان متقدمتان progressive مغذاتان ومتماثلتان تردداً، وتنتشر إحداهما في اتجاه يعاكس انتشار الأخرى، وينتج من تراكبهما أو تداخلهما تكوّن أجزاء تهتز بسعة عظمى تسمى بطون الاهتزاز antinodes ويرمز لها بالحرفA، يفصل ما بينها بالتناوب أجزاء تنعدم أو تكاد تنعدم فيها سعة الاهتزاز، وتسمى العقد nodes ويرمز لها بالحرف N. وتظهر الموجة المستقرة وكأنها تهتز مراوحة في مكانها، لذلك وُصفت بالمستقرة، وهي تختلف بذلك عن الموجة المتقدمة التي تبدو كأن سعة الاهتزاز فيها هي التي تنتشر وتتقدم. وتكون المسافات بين العقد متساوية كما هو مبين في الشكل 1، ويؤلف الاهتزاز ما بين عقدتين متجاورتين ما يشبه المغزل.

Standing waves in a string — the fundamental mode and the first 6 overtones.

A two-dimensional standing wave on a disk; this is the fundamental mode

A higher harmonic standing wave on a disk with a node at the center of the drum.

 الوصف الرياضي

وتحدث الأمواج المستقرة في كل الحركات الموجية سواء أكانت ميكانيكية أم صوتية أم ضوئية أم كهرمغنطيسية. ويعطى مطال الاهتزاز y في أي موجة متقدمة بالعلاقة التالية:

Let the harmonic waves be represented by the equations below:

$y_{1}\;=\;y_{0}\,\sin(kx-\omega t)$

و

$y_{2}\;=\;y_{0}\,\sin(kx+\omega t)$

حيث:

• y₀ هي سعة الموجة,
• ω (تسمى التردد الزاوي، مقاساً ب radian في الثانية) هي 2π مضروبة في التردد (بالهرتس),
• k (ويسمى رقم الموجة ويقاس ب radians في المتر) هي 2π مقسومة على طول الموجة λ (ب المتر)، و
• x و t هما متغيران للموقع الطولي والزمن، على الترتيب.

لذلك فمعادلة الموجة الناتجة y ستكون مجموع y₁ و y₂:

$y\;=\;y_{0}\,\sin(kx-\omega t)\;+\;y_{0}\,\sin(kx+\omega t).$

وباستخدام trigonometric identity للتبسيط، يمكن وصف الموجة المستقرة كالتالي:

$y\;=\;2\,y_{0}\,\cos(\omega t)\;\sin(kx).$

حيث a: السعة وl: طول الموجة و v: سرعة الانتشار وx: البعد عن نقطة اتُّخذت مبدءاً للاهتزاز. فإذا انعكست هذه الموجة ناظمياً عند نهاية وسط الانتشار انعكاساً كلياً أو جزئياً بحسب شروط النهاية، تولّدت موجة منعكسة تكون معادلتها، إذا كان الانعكاس كلياً، كما يلي:

وينتج إذن من تراكب الموجتين الواردة والمنعكسة أو تداخلهما موجةٌ تكون معادلتها كما يلي، وفقاً لمبدأ التراكب (الانضمام) superposition:

وهي موجة مستقرة ينعدم الانزياح أو الاهتزاز فيها عند نقاطٍ تبعد عن نهاية الانعكاس بالأبعاد وهي مواضع العقد.

ويكون الاهتزاز أعظمياً وسعته 2a عند نقاط تكون أبعادها وهي مواضع مراكز البطون، وتتناقص سعة الاهتزاز باطّراد على جانبيْ البطن حتى تنعدم عند العقدة. وإذا كان الانعكاس يتم عند نهاية طليقة كانت الموجة الواردة والموجة المنعكسة متفقتيْن في الطور عند الانعكاس فيتولد بطن اهتزاز عند الطرف العاكس، ولكن يظل مظهر الموجة المستقرة كما كان وكذلك المسافات الفاصلة بين العقد، غير أن مواضع هذه العقد يتعيّن بالأبعاد

ولعل أفضل تجربة يتضح فيها تكوُّن الأمواج المستقرة هي تجربة مِلْد Melde التي يُثبَّت فيها طرف خيط أفقي بأحد فرعيْ شوكةٍ رنانة ويمر طرفه الآخر على بكرة، وينتهي بكفة تُحمَّل بالأوزان. تُجعل الرنانة تهتز في مستوٍ متعامد مع الخيط وتُغذَّى اهتزازاتها كهربائياً، فيهتز الخيط بتردد يساوي تردد الرنانة. ولما كان طول الخيط L ثابتاً وكذلك كتلة واحدة الطول m منه، فإن المتغير الوحيد هو قوة الشد F التي يحدثها الوزن M. فمن أجل وزنٍ معين مناسب ينقسم الخيط المهتز إلى عدد صحيح من المغازل، كما هو مبين في الشكل 2. ويكون البعد ما بين عقدتين متعاقبتين l/2، كما ذكر من قبل؛ وبزيادة الوزن أو إنقاصه يتغير عدد المغازل P (الشكل 1). فتتحقق معه العلاقة: ثابت = FP2، حيث F قوة شد الخيط. وتنتج هذه العلاقة من قانون الأوتار المهتزة، وهو:

حيث يدل n على تردد الرنانة.

 الموجات الطبيعية

سمة الغيمة المسدسة الأضلاع عند القطب الشمالي لكوكب زحل يـُعتقد أنه نوع من أنماط الموجات الراكدة.

إن تجربة مِلْد تظهِر الأمواج المستقرة الناجمة عند تراكب أو تداخل اهتزازتين عرضانيتين أو تداخلهما (أي منحى الاهتزاز في كلٍ منهما عمودي على منحى انتشار الاهتزاز) غير أنه يمكن أيضاً توليد أمواج مستقرة نتيجة تراكب موجتين طولانيتين (منحى الاهتزاز يتفق مع منحى الانتشار) مثل الموجات الصوتية. وأشهر تجربة في هذا المجال تجربة أنبوب كونْدِت Kundt؛ وهو أنبوب أسطواني زجاجي سُدَّتْ إحدى نهايتيه وجُعل عند النهاية الأخرى منه منبع صوتي ، يملأ الأنبوب غازاً ما، وتنثر فيه كمية صغيرة من مسحوق خفيف مثل ذرات الليكوبوديوم أو الفلين نثراً منتظماً على طول الأنبوب. فإذا جُعل طول الأنبوب موافقاً لحدوث عدد صحيح من المغازل حين يصدر الصوت، اهتزت ذرات الفلين في أماكن البطون وكوّنت عدة أكوام متساوية الأبعاد (الشكل 3). ويمكن أن يكون المنبع الصوتي قضيباً ثُبِّت في منتصفه C وزُوِّد أحد طرفيه D بقرص يكاد يسد الأنبوب، ويتم توليد الصوت بِدلْك هذا القضيب بقماش مقلّف أو مصمَّغ. كذلك قد يكون المنبع الصوتي قرص هاتف متصلاً بهزازة مناسبة، أو بلورة كوارتز تولّد صوتاً تردده فوق الصوتي. ويستفاد من تجربة أنبوب كوندت في قياس سرعة الصوت في الغازات v ودراسة تغيّر هذه السرعة بتغير شروط الغاز، وذلك اعتماداً على العلاقة v =l n. إن ما يحدث في أنبوب كوندت يحدث مثله في كل الآلات الموسيقية الهوائية، إذ تتكون بالطريقة نفسها أمواج طولانية مستقرة في الهواء الذي يملأ الآلة من أجل كل نغمة تصدر منه.

 الموجات الضوئية

وتحدث الموجة الضوئية المستقرة، على غرار ما في تجربة مِلْد، نتيجة تداخل الموجة الضوئية الوحيدة اللون المنعكسة مع الموجة الواردة، إلا أن مشاهدة هذه الموجة أصعب بكثير، لأن طول المغزل في هذه الحالة من مرتبة أجزاء المكرون (10-4مم)، لصغر طول الموجة الضوئية (0.4-0.7 مكرون). وقد أمكن في أواخر القرن التاسع عشر تصوير الأمواج المستقرة باستعمال فِلمْ طبقته الحساسة دقيقة الحبيبات، وأدى ذلك إلى اكتشاف طريقة دقيقة في التصوير الملوَّن (طريقة لبمان Lippmann). وتجدر الإشارة أخيراً إلى أن الأمواج المستقرة الكهرمغنطيسة تتكون على طول هوائيات البث الإذاعي aerials.

 انظر أيضاً

• قائمة مواضيع الموجات:

Amphidromic point, Clapotis, Longitudinal mode, Modelocking, Seiche, Trumpet, Voltage standing wave ratio, Wave

• List of electronics topics:

Cavity resonator, Characteristic impedance, Cymatics, Impedance, Normal mode

 المصادر والهامش

• خالد عقيل. "الأمواج المستقرة". الموسوعة العربية. Retrieved 2009-06-20.

 وصلات خارجية

• Vibrations and Waves - a chapter from an online textbook
• Standing Waves experiment Shows how the point moves with frequency change.
• Java applet of standing waves on a vibrating string.
• Java applet of transverse standing wave
• Java applet showing the production of standing wave on a string by adjusting frequency

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 للاستزادة

ـ الاهتزازات والأمواج (1)، ترجمة تربدار وقسام ومعصراني (مطبوعات جامعة دمشق، 1981). ـ الفيزياء الحديثة للجامعات، الجزء الأول (الميكانيك والصوت)، ترجمة قدورة وسمان وحصري (مطبوعات جامعة دمشق 1973).