موجة كهرومغناطيسية
| كهرومغناطيسية | ||||||||||
| ||||||||||
كهرباء • مغناطيسية
| ||||||||||
موجات كهرومغناطيسية (Electromagnetic Waves) تبعث الدوائر الكهربائية التي تحمل تيارات متذبذبة عالية التردد الطاقة على هيئة مجالين يعتمدان على بعضهما, أحدهما كهربائي والأخر مغناطيسي, ويميل كل منهما على الأخر.
الفيزياء
تحتل الأمواج الكهرمغنطيسية مجالاً واسعاً يمتد من الموجات الراديوية والهرتزية، والتي هي أطولها موجة، إلى أشعة غاما g وهي أقصرها موجة. ويبين الشكل 2 تصنيف هذه الأمواج بدلالة الطول الموجي l في الخلاء مقدراً بالأمتار، وبدلالة تردداتها مقدرة بالهرتز. ويظهر في هذا الشكل الاشتراك في الطول الموجي.[1]
تصنيف الموجات الكهرمغنطيسية بدلالة طول الموجة l في الخلاء مقدراً بالأمتار
إن الأمواج الكهرمغنطيسية، بأصنافها كلها، تتفق فيما بينها بالخواص العامة للأمواج (الانتشار، والانعكاس، والانكسار، والتداخل، والانعراج، والاستقطاب وغيرها). ويمكن استنتاج هذه الخواص من معادلات ماكسويل. ولكن أصناف الأمواج الكهرمغنطيسية تختلف فيما بينها من حيث مصدرها ومنشؤها ومن حيث كشفها. فالأمواج الراديوية والهرتزية تولدها هزَّازات إلكترونية أو حركة الجسيمات المشحونة في حقول مغنطيسية، والضوء المرئي وغير المرئي تولده الأجسام المتوهجة والغازات المتأينة (المتشردة) وينشأ عن تغير في حالات الطاقة للذرات والجزيْئات، والأشعة السينية تنشأ عن اصطدام إلكترونات سريعة ذات طاقة عالية بمادةٍ ما في شروط معينة، وأشعة غاما تصدر تلقائياً من العناصر ذات النشاط الإشعاعي وتنشأ عن تفكك disintegration هذه العناصر.
نبذة تاريخية

في عام 1864م توقع العالم الفيزيائي البريطاني كلارك ماكسويل وجود الموجات الكهرومغنطيسية. افترض ماكسويل أن المجالين المغنطيسي والكهربائي يعملان سويًا على إنتاج طاقة إشعاعية. وعرف الضوء على أنه أحد أنواع الموجات الكهرومغنطيسية كما توقع وجود موجات غير مرئية.
وفي عام 1887م أكد عالم الفيزياء الألماني هينريتش هرتز ما توقعه ماكسويل. فقد بيّن أن تذبذب شحنة كهربائية تنتج عنه موجات كهرومغنطيسية أطول بكثير من موجات الضوء المرئي. وقد قاد اكتشاف هرتز هذا إلى تطوير المذياع والتلفاز.
المجال المغناطيسي المتغير يولد المجال الكهربائي, كما أن المجال الكهربائي المتغير يولد المجال المغناطيسي.
الإشعاع يتكون من موجات كهرومغناطيسية تتحرك في الفضاء بسرعة الضوء أي بسرعة 299796 مليون متر في الثانية أو بسرعة 186284 ميل في الثانية.
أثبت العالم فرداي بالتجربة العلاقة بين الظاهرتين المغناطيسية والكهربائية, كما أفترض العالم جيمس ماكسويل وجود الموجات الكهرومغناطيسية وأن لها طبيعة مماثلة لطبيعة الضوء, وأن الموجات الضوئية هي على صورة الموجات الكهرومغناطيسية.
أثبت العالم هرتز بالتجربة هذه النظرية الرياضية البحتة بعد سبعة سنوات من وفات ماكسويل.

سرعة الإنتشار
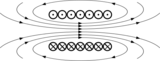
الموجة الكهرمغنطيسية electromagnetic waves هي انتشار اضطراب الحقل الكهربائي المصحوب باضطراب الحقل المغناطيسي . ويكون الحقلان متعامدين فيما بينهما وعموديين على منحى الانتشار propagation (الشكل 1).
وتنتشر الموجة بسـرعة V، تعطى بالعلاقة
حيث Î السماحية permetivity الكهربائية للوسط، و m: نفوذيته permeability المغناطيسية، وتبلغ سرعة انتشار الموجة في الخلاء C= 3×810 متر/ثانية. والموجة الكهرمغناطيسية عرضانية (منحى الاهتزاز فيها عمودي على منحى الانتشار)، فهي لذلك تُسْتَقْطَب بخلاف الأمواج الطولانية (الأمواج الصوتية) التي لا تقبل الاستقطاب.
وللأمواج الكهرمغنطيسية ما يميز الأمواج عامة، فالطول الموجيl هو المسافة الخطية التي تقطعها الموجة (الحقلان→E و→H معاً) في الزمن اللازم للقيام باهتزازة كاملة والذي يسمى الدور T، أي أن l=VT حيث V: سرعة انتشار الموجة الكهرمغنطيسية في الوسط المعتبر. أما تردد (تواتر) الموجة الكهرمغنطيسية فهو عدد الاهتزازات في واحدة الزمن (الثانية)، أي أن
طاقة الأمواج الكهرمغنطيسية
إذا كان الحقل الكهربائي في نقطة ما يساوي E وكان الحقل المغنطيسي يساوي H، فإن الطاقة الكهرمغنطيسية W في واحدة الحجوم تعطى بالعلاقة التالية: w= Î E2 ولما كان:
أمكن أن يكتب أيضاً
إن هذه الطاقة ترافق الحقلين →Eو →H، فهي إذاً تنتقل بسرعتهما C في الخلاء. لهذا يمكن أن تُمثَّل اتجاهياً باستعمال متجه بويْنتِنْغ Poynting، وهو
→P = →E´ →H و ، باستقامة C وبالاتجاه نفسه. وينتج من ذلك أن:
إن هذا التمثيل الموجي للطاقة غير كاف لتفسير كل الظواهر المتصلة بالأمواج الكهرمغنطيسية ولاسيما الظاهرة الكهربائية الضوئية. فهذه الظاهرة لا يمكن تفسيرها إلا على أساس من أن الضوء يتكون من جسيمات (فوتونات) إذا اصطدمت بمادة ما في شروط معينة، اقتلعت منها بعض إلكتروناتها، لذلك ينبغي أن يُشرَك مع هذا التمثيل تمثيل مكمم quantised، أي أن تجزأ الطاقة إلى حبيبات هي الفوتونات، حيث ينقل كل فوتون منها طاقة تساوي e = hf، ويدل f على تردد الموجة الكهرمغنطيسية و h على ثابت بلانك.
الطيف الكهرومغنطيسي

γ = Gamma rays
HX = Hard X-rays
SX = Soft X-Rays
EUV = Extreme ultraviolet
NUV = Near ultraviolet
Visible light
NIR = Near infrared
MIR = Moderate infrared
FIR = Far infrared
Radio waves:
EHF = Extremely high frequency (Microwaves)
SHF = Super high frequency (Microwaves)
UHF = Ultrahigh frequency (Microwaves)
VHF = Very high frequency
HF = High frequency
MF = Medium frequency
LF = Low frequency
VLF = Very low frequency
VF = Voice frequency
ELF = Extremely low frequency
يتكون من نطاقات من الأطوال الموجية المختلفة. وأهم أنواع الموجات الكهرومغنطيسية مرتبة ترتيبًا تصاعديًا حسب الطول الموجي هي أشعة جاما، فالأشعة السينية، فالضوء فوق البنفسجي، فالضوء المرئي فالأشعة تحت الحمراء، فالموجات المتناهية الصغر، ثم موجات الراديو. ويبلغ طول أشعة جاما حوالي10-11 م بينما يبلغ طول بعض موجات الراديو الطويلة أكثر من 10,000كم.
ولكل أنواع الموجات الكهرومغنطيسية خواص الضوء المرئي. فهي تنعكس وتنتشر وتنكسر. ويكون اتجاه المغنطيسية في كل الموجات الكهرومغنطيسية عموديًا على اتجاه حركتها، بينما يكون اتجاه القوة الكهربائية عموديًا على اتجاه القوة المغنطيسية واتجاه حركة الموجات. وتساوي شدة القوة المغنطيسية دائمًا شدة القوة الكهربائية.
استخدامات الموجات الكهرومغنطيسية
يستخدم الأطباء أشعة جاما، التي يشعها الراديوم، في علاج السرطان. ويستخدمون كذلك الأشعة السينية لعلاج السرطان، كما يستخدمونها في تحديد مكان الاضطرابات الداخلية وتشخيصها. وتُستخدم الأشعة فوق البنفسجية في المصابيح الشمسية، وفي المصابيح الفلورية، وكمطهر. أما الموجات تحت الحمراء، التي تنبعث من الأجسام الساخنة، فتُستخدم في علاج الأمراض الجلدية، وصقل المينا. وتستخدم موجات المايكروويف؛ أي الموجات المتناهية الصغر، لطهو الطعام، بينما تُستخدم موجات الراديو في الإذاعة المسموعة والمرئية.
ويعتمد الاستخدام التقني للموجات الكهرومغطيسية على السهولة التي يمكن بها التعرف على الأطوال الموجية المختلفة وإنتاجها. ويرتبط الطول الموجي بمعدل اهتزاز الإلكترونات في مصدر الطاقة، فكلما كان الاهتزاز أبطأ ازداد الطول الموجي. وأسهل الموجات إنتاجًا هي الموجات الطويلة. وقد بدأ استخدام موجات الراديو في الاتصالات في أوائل القرن العشرين، ولم يحدث استغلال فعّال للموجات القصيرة إلا بعد تطوير بعض النبائط كالكلايسترون وهو نوع من أنواع صمامات الموجات الدقيقة انظر: الصمام المفرغ. وقد أدى تطوير الليزر في أوائل الستينات من القرن العشرين إلى استخدامات جديدة للموجات القصيرة. فعلى سبيل المثال، يمكن الليزر الأشعة فوق البنفسجية وتحت الحمراء من نقل الرسائل الصوتية والإشارات التلفازية.
انظر ايضا
- Bioelectromagnetism
- Bolometer
- Control of electromagnetic radiation
- Electromagnetic pulse
- Electromagnetic radiation and health
- Electromagnetic spectrum
- Electromagnetic wave equation
- Finite-difference time-domain method
- Helicon
- Klystron
- Light
- Maxwell's equations
- Photon polarization
- Radiant energy
- Radiation reaction
- Sinusoidal plane-wave solutions of the electromagnetic wave equation
مصادر
- ^ إلياس أبو عسلي. "الأمواج الكهرمغنطيسية". الموسوعة العربية. Retrieved 2012-04-05.
- Hecht, Eugene (2001). Optics (4th ed.). Pearson Education. ISBN 0-8053-8566-5.
- Serway, Raymond A. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8.
- Reitz, John (1992). Foundations of Electromagnetic Theory (4th ed.). Addison Wesley. ISBN 0-201-52624-7.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Jackson, John David (1999). Classical Electrodynamics (3rd ed.). John Wiley & Sons. ISBN 0-471-30932-X.
- Allen Taflove and Susan C. Hagness (2005). Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed. Artech House Publishers. ISBN 1-58053-832-0.
مراجع للإستزادة
- إلياس أبو عسلي، الإلكتروديناميك (مطبوعات جامعة دمشق 1970).
- أدهم السمان، الكهرمغنطيسية (مطبوعات جامعة دمشق 1980).
وصلات خارجية
- Electromagnetism - a chapter from an online textbook
- Electromagnetic Radiation - an introduction for electrical engineers
- Electromagnetic Waves from Maxwell's Equations on Project PHYSNET.
- Radiation of atoms? e-m wave, Polarisation, ...










