عزم مغناطيسي
| كهرومغناطيسية | ||||||||||
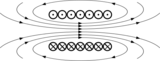
| ||||||||||
كهرباء • مغناطيسية
| ||||||||||
في الفيزياء والفلك والكيمياء ، والهندسة الكهربائية ، فإن مصطلح العزم المغناطيسي لحظة النظام (مثل حلقة من التيار الكهربائي ، قضيب المغناطيس ، الكتروني ، جزىء ، أو كوكب) وعادة ما يشير إلى ثنائي القطب المغناطيسي لحظة ، و هي مقياس لمدى قوة النظام صافي المصدر المغناطيسي. على وجه التحديد ، لحظة ثنائي القطب المغناطيسي يحدد مساهمه المنظومه الداخلية إلى الخارجية مغناطيسيه dipolar المجال المغناطيسي التي ينتجها النظام (أي عنصر من المجال المغناطيسي الخارجي ان تنخفض مع المسافة كما هيسكعلا مكعب). Dipolar اي مجال مغناطيسي النمط المتماثلة فيما يتعلق تناوب حول محور معين ، ولذلك فقد جرى العرف على وصف لحظة ثنائي القطب المغناطيسي ان يخلق هذا المجال.. كما واسطة مع الاتجاه على طول هذا المحور. لquadrupolar ، octupolar ، وأعلى من اجل multipole المغناطيسي لحظات ، انظر multipole التوسع.
الوحدات
| 1 م2·أ = 1 ج/ت. |
نوعان من المصادر المغناطيسية
العزم المغناطيسي والعزم الزاوي
أمثلة للعزم المغناطيسي
العزم المغناطيسي للملفات الكهربائية
Magnetic moment of a current-carrying loop depends on its area and current. For example, the magnitude of magnetic moment for a single-turn circular coil of radius 5 cm carrying 1 A of current is determined as:
The vector of this moment is pointing perpendicular to the plane of the loop, in the direction of the magnetic field at the center of the loop (see right-hand rule). Knowing this value of the loop's magnetic moment can be used to establish the following facts:
- At distances R much larger than the radius of the loop r = 0.05 m, the magnetic field produced by this loop will drop off as:
- (along the loop's axis)
- و
- (in the loop's plane). Minus indicates the field direction opposite to the axial case.
- In the Earth's magnetic field of 0.5 G (5×10-5 T) perpendicular to the loop's axis, the loop (as well as the Earth) will experience a torque of
- If such compass is allowed to orient its axis parallel to the Earth's field, the amount of energy released from the compass-Earth system is given by:
- J. This energy can be dissipated into heat to overcome friction in the compass suspension system.
العزم المغناطيسي للملفات اللولبية
Magnetic moment of a multi-turn coil (or solenoid) is determined as the vector sum of the moments of individual turns. In the case of identical turns (single-layer winding), it is equal simply to the individual turn's moment multiplied by the total number of turns in the solenoid. Once the value of the total magnetic moment is found, it can be used to establish the far field, the torque, and the stored energy in the external field in the same way as for the single-turn loop.
Magnetic dipoles
العزم المغناطيسي للذرات
حيث J is the total angular momentum quantum number, gJ is the Landé g-factor, and μB is the Bohr magneton. The component of this magnetic moment along the direction of the magnetic field is then:[1]
حيث m يسمى رقم الكم المغناطيسي أو رقم الكم الإستوائي، الذي يمكن أن يتخذ أيٍ من قيم 2J+1: -J, −(J-1), … , (J−1), J.[2] The negative sign occurs because electrons have negative charge.
where γ =gyromagnetic ratio, m = magnetic moment, λ = damping coefficient and Heff = effective magnetic field (the external field plus any self-field), and '×' = vector cross product. The first term describes precession of the moment about the effective field, while the second is a damping term related to dissipation of energy caused by interaction with surroundings.
العزم المغناطيسي للإلكترونات
The magnetic moment of the electron is
حيث
- is the Bohr magneton, S is electron spin,
and the electron g-factor is
- in Dirac mechanics, but is slightly larger,
- in reality due to quantum electrodynamics effects.
- ^ Paul Allen Tipler, Ralph A. Llewellyn (2002). Modern Physics (4 ed.). Macmillan. p. 310. ISBN 0716743450.
- ^ JA Crowther (2007). Ions, Electrons and Ionizing Radiations (reprinted Cambridge (1934) 6 ed.). Rene Press. p. 277. ISBN 1406720399.













