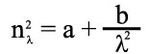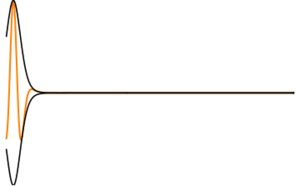تشتيت الضوء

هذا المقال هو عن dispersion of waves in optics. إذا كنت تريد other forms of dispersion، انظر Dispersion (disambiguation).

In a prism, material dispersion (a wavelength-dependent refractive index) causes different colors to refract at different angles, splitting white light into a rainbow.

A compact fluorescent lamp seen through an Amici prism

تشتيت أو تشتت الضوء أو التقزح dispersion هو فصل الضوء إلى ألوانه. تنكسر الألوان بحسب قيمها المختلفة، فلكل لون درجة انكسار معينة. في تشتت الضوء الأبيض يفصل إلى الألوان في الطيف المرئي. يتشتت الضوء عبر المنشور، كما يمكن للحيود والاستطارة أن يسببا تشتت الضوء.

وتعد تجربة إسحاق نيوتن التي استعمل فيها موشوراً ليبيِّن أن ضوء الشمس هو ضوء مركب من عدة ألوان، أولى تجارب التبدد التي فرقت الضوء إلى مركباته. تسمى مركبات ضوء ما بطيفه spectrum. ويسمى العلم الذي يعالج دراسة الأطياف علم الأطياف spectroscopy. كما يدعى الجهاز المستخدم لدراسة الأطياف بالمطياف spectroscope. يمثل علم الأطياف فرعاً واسعاً من العلوم الفيزيائية أسهم إسهاماً فعالاً في فهم ما يحدث في باطن الشمس والنجوم اعتماداً على فهم أطياف الذرات والجزيئات على الأرض. وما زالت المواشير تستخدم في العديد من أجهزة التحليل الطيفي رغم وجود أدوات تفريق أفضل اليوم مثل شبكة الانعراج. ويعتمد اختيار الجهاز على مقدرة الفصل المطلوبة للتطبيق.

 قرينة الانكسار

قرينة انكسار وسط معيّن n هي نسبة سرعة الضوء في الخلاء إلى سرعته في هذا الوسط. وتختلف سرعة انتشار كل مركبة من مركبات الضوء ذات الطول الموجي λ عن غيرها لذلك يضاف دليل إلى قرينة الانكسار فتكتب nλ. فإذا ما ورد شعاع ضوئي بزاوية معينة على سطح فاصل بين وسطين انكسر هذا الشعاع بزاوية تحددها قرينة الانكسار لكل من الوسطين بحيث تكون نسبة جيبي الزاويتين، زاوية الورود وزاوية الانكسار، كمقلوب نسبة قرينتي الانكسار، لذلك وبسبب اختلاف القرينة اختلافاً طفيفاً من لون إلى آخر تظهر عدة أشعة مفرقة بألوان مختلفة.

إن تبدد الضوء نتيجة من نتائج تفاعل الضوء مع المادة. ويحدث لجميع الأمواج الكهرمغنطيسية عموماً لكن مقداره يختلف باختلاف موقع الطول الموجي من الطيف الكهرمغنطيسي مقارنة بطول مميز للمادة، مثل المسافة بين الذرات أو موقع تواتر المركبة الكهرمغنطيسية مقارنة بتواتر مميز للمادة، مثل تواتر اهتزاز جزيئات المادة الخاص بها. إن تغير قرينة الانكسار dnλ ومن ثم تغير سرعة انتشار مركبة ذات لون محدد بـ l مع تغير التواتر (التردد) الزاوي dw أي النسبة ليس كبيراً وقد تكون موجبة فيسمى التبدد عندئذ تبدداً عادياً وقد تكون سالبة فيسمى التبدد عندها تبدداً شاذاً، وغالباً ما يحدث التبدد الشاذ بجوار تواتر يكون عنده الامتصاص absorption شديداً. ويعد الامتصاص نتيجة أخرى من نتائج تفاعل الضوء مع المادة وستظهر علاقة التبدد بالامتصاص عند النظر في هذا التفاعل على المستوى الذري أو الجزيئي.

 عامل الامتصاص والتوهين

الامتصاص الضوئي هو تحوّل من شكل الطاقة الكهرمغنطيسية إلى أشكال أخرى للطاقة. ويعبّر عن مقدرة وسط ما على الامتصاص بمعامل ( وهو ثابت التناسب بين الشدة الضوئية الضائعة dI والطول الذي اجتازه الضوء dx والشدة الضوئية I (الطاقة التي تعبر واحدة المساحة خلال واحدة الزمن بصورة عمودية على المساحة) فنكتب: وتشير الإشارة السالبة إلى التناقص وبالمكاملة نجد:

يعتمد عامل الامتصاص ß بصورة رئيسة على طول موجة الضوء وقد يعبّر عن الامتصاص أحياناً بمقلوب معامل الامتصاص الذي يسمى طول (عمق) الاختراق penetration (depth) length ويرمز له عادة بالحرف L وأحياناً أخرى بطول الانطفاء الذي يساوي 4.6L إذ يقابل هذا الطول إذا ما اجتازه الضوء نقصاناً نسبياً في الشدة لتصبح مساوية واحد بالمئة من الشدة الأصلية. يتضافر هذا العامل مع عامل آخر فيسبب نقصاناً في الشدة وفق الاتجاه المدروس فهو لا يمثل تغيراً في شكل الطاقة وإنما تغيراً في منحاها وابتعادها عن الاتجاهات المحدّدة بقانوني الانعكاس والانكسار ويسمى عامل الانتثار َß وهو يسلك سلوك ß في الحالة العامة ويسمى مجموعهما عامل التوهين attenuation أو التخامد γ فيحل هذا العامل محل b في العلاقة السابقة أي َγ=ß+ß. تصنف الأوساط المادية المختلفة وفق هذا العامل في صنفين رئيسين وضمن المجال المرئي من الأطوال الموجية: أوساط شفافة وأوساط عاتمة. يكون عامل التوهين في الأولى ضعيفاً كما في الزجاج العادي الذي يقدر طول انطفائه ببضع عشرات السنتمتر ويمكن إذا ما أخضع لتنقية عالية أن يصبح بضع عشرات الكيلو متر كما في حالة [بالألياف الضوئية]]. أما عامل توهين الصنف الثاني فلا يتعدى بضعة أجزاء الملمتر كما في حالة المعادن. تعزى أسباب الامتصاص على المستوى الذري أو الجزيئي إلى حدوث تجاوبات تقابل انتقالات إلكترونية من سوية إلى أخرى أو انتقالات بين سويات اهتزازية ودورانية لجزيئات الوسط أو سلوك مشترك للإلكترونات أو للذرات المترابطة المكوّنة للوسط. أما أسباب التبعثر وكذلك بعض أسباب الامتصاص فتكون نتيجة وجود شوائب وفقاعات في الأجسام الصلبة، وغالباً ما تظهر شوائب معينة امتصاصاً عند مجال محدّد من طول الموجة فيكون الامتصاص انتقائياً فإضافة بضعة أجزاء في المئة من أكسيد الحديد يعطي الزجاج اللون الأخضر الغامق وتعطيه إضافة نسبة مقاربة من أكسيد النيكل اللون الأصفر، وتستخدم مثل هذه الخواص في الترشيح الضوئي. وقد يحدث بالنسبة لبعض المواد كالفُسْفور أن تمتص طاقة ذات طول موجي معين ثم تعود لتصدرها بطول موجي مختلف، تألق الوسط. ونذكر أن العين البشرية غير قادرة على التحليل الطيفي لكنها تميز تدرج الألوان واللمعان المرتبطين بالشدة، فيختلف عامل امتصاص الخلايا العصوية عن عامل امتصاص المخاريط اختلافاً واضحاً فتكون نهايات الامتصاص العظمى لها متباينة.

 القدرة المبدّدة dispersion power

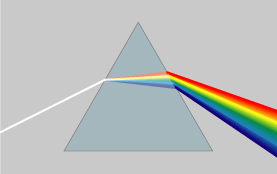
قد لا تؤثر الإضافات تأثيراً كبيراً على عامل الامتصاص لكنها قد تؤثر تأثيراً ملحوظاً في قرينة الانكسار مغيرة قيمتها وكان للزجاج الحظ الأوفى لهذه الدراسات بغية صنع مواشير ذات تبديد عالٍ فصنع منه عدة أنواع وعرفت القدرة المبدّدة W للتمييز بينها بالعلاقة:

ملف:3120-6.jpg

حيث تشير الأدلة F,D,C إلى أطوال موجية محدّدة يدعوها البعض خطوط فراونهوفر ويظهر الجدول 1 قيم هذه الأطوال الموجية إضافة إلى قيم قرائن انكسار أنواع مختلفة من الزجاج والقدرة المبدّدة لكل منها وقد أضيف للجدول مادتا البنزين والماء للمقارنة:

خطوط فراونهوفر

C

D

F

القدرة المبددة

الطول الموجي مقدراً بالنانومتر

656.3

589.0

486.2

W

الزجاج التاجي

(Ca+++K++Na+)

1.514

1.517

1.524

0.0193

زجاج الفلنت (الصخري)

(Pb+++k++Na+)

1.622

1.627

1.639

0.0271

البنزين

1.497

1.503

1.514

0.0338

الماء

1.332

1.334

1.338

0.018

الجدول (1) قرائن الانكسار لمواد مختلفة

ويلاحظ أن جميع هذه المواد ذات تبدد طبيعي فقرينة انكسارها تنقص مع ازدياد الطول الموجي ويعبر عن هذا أحياناً بعلاقة كوشي Cauchy التجريبية:

يفسّر في الواقع حدوث قوس قزح نتيجة ارتداد (انعكاس) ضوء الشمس عن قطرات الماء المعلقة في الهواء بعد أن يعاني انكسارين أو أكثر عند السطح الفاصل بين الماء والهواء، فاختلاف قرينة الانكسار باختلاف الطول الموجي هو الذي يفرق ضوء الشمس إلى مركباته المتدرجة من البنفسجي حتى الأحمر.

 قرينة الانكسار واستقطابية المادة وعلاقتها بتبدد الضوء

حين تسقط موجة كهرمغنطيسية أو ضوء على مادة ما فإنها تحرِّض اهتزازات الجسيمات المشحونة فيها وخاصة إلكترونات الذرات والأيونات المكوِّنة للجزيئات فتصدر بدورها أمواجاً ثانوية مبعثرة في جميع الاتجاهات. تتراكب هذه الأمواج مع الموجة الأصلية لتعطي موجة محصِّلة تظهر بسرعة انتشار مختلفة عن قيمتها في الخلاء، ويظهر هذا جلياً عند السطح الفاصل بين الخلاء والمادة، في حين لاتتغير سرعة انتشار الضوء ولا اتجاهه حين يسير في وسط مادي متجانس. إن الحقل الكهربائي والحقل المغنطيسي المعبّرين عن أثر الموجة الكهرمغنطيسية في الوسط وتغيراتهما مع الزمن محكومان بمعادلة الانتشار لكل منهما اللتان تستنتجان مما يعرف بمعادلات مكسويل. تظهر علاقة سرعة الانتشار بخواص الوسط المادي الكهربائية ممثلة بالعازلية الكهربائية ε dielectric constant والسماحية المغنطيسية μ magnetic permitivity على الشكل: وفيها c سرعة الضوء في الخلاء. ولما كانت (للأوساط الشفافة قريبة من الواحد نرى أن قرينة الانكسار مرتبطة بالعازلية الكهربائية وفق العلاقة: بصورة أولية؛ وستظهر علاقة التبديد والامتصاص بدراستها على المستوى الذري. فقد عُرّفت ε في البدء في حالة حقول كهربائية ساكنة ثم عدّلت لتشمل حالة حقول كهربائية مهتزة، كما في حالة الضوء، فظهر جزءان لها الأول حقيقي يمثل تغير سرعة الانتشار والآخر تخيلي يمثل الامتصاص.

إن الذرات والجزيئات المكونة للمادة ليست صلدة تماماً لا يمكن تغيير الأبعاد فيما بينها أو بين إلكترونات الذرة ونواتها، ومن ثم حين تطبيق حقول كهربائية ساكنة (لا تتغير مع الزمن) على مجموعة شحنتين مثل إلكترون شحنته سالبة ونواة شحنتها موجبة ستنزاح الشحنة السالبة في اتجاه معاكس لانزياح الشحنة الموجبة عند تطبيق الحقل، ومن ثم نقول إن مركزي الشحنتين قد انزاحا عن بعضهما، بعد أن كانا متطابقين في البدء، وكوّنا ما يعرف بثنائي القطب الكهربائي المتحرض ويمثل بمتجهة تبدأ من مركز الشحنة الموجبة وتنتهي عند مركز الشحنة السالبة، ويكون البعد بين المركزين صغيراً بالمقارنة مع الأبعاد التجريبية. وقد يوجد أحياناً ثنائيات قطب في تركيب المادة كأن تكون مكوّنة من أقطاب موجبة وأقطاب سالبة مرتبة كما في حالة بعض الجزيئات فيكون تأثير تطبيق الحقل الكهربائي محاولة جعل ثنائي القطب مصطفاً باتجاه الحقل المطبق وفي كلتا الحالتين يظهر تأثير ثنائيات القطب المجاورة لثنائي قطب مدروس على شكل حقل إضافي يسمى شعاع الاستقطاب لواحدة الحجم، فإذا ما أضيف إلى الحقل المطبق حصلنا على حقل التحريض الكهربائي الإجمالي و ثابتة تتعلق بالوحدات المستخدمة.

وغالباً ما يكون p متناسباً مع الحقل المطبق على الصورة: ′α= فتدعى′α استقطابية المادة وتظهر علاقتها بالعازلية الكهربائية وفق التالي:

ملف:3120-12.jpg

يتمثل تأثير الوسط إذن بكتابة ε مكان εo المقابلة في الخلاء وتقاس العازلية الكهربائية عادة بقياس تغير سعة capacitance مكثفة كهربائية نتيجة وضع الوسط المادي بين لبوسيها مكان الخلاء، فيظهر ′α و ε كآثار جهرية تقاس مباشرة.

إن دراسة الحقول الكهربائية المهتزة (المتغيرة مع الزمن) وتأثيراتها من خلال قياس ε المقابلة أعقد من ذلك وبالتالي سيُنظر أولاً فيما يحدث على مستوى ثنائي قطب واحد سواء كان أيونين مختلفي الشحنة أو إلكترون سالب ونواة موجبة ونأخذ تأثير الجوار باستخدام الحقل الإجمالي المحلّي مما يمكّننا بعد ذلك الحصول على السلوك الجهري بضرب النتيجة بعدد الثنائيات في واحدة الحجم.

إذا ما أُزيح إلكترون كتلته m عن وضعه التوازني فسيخضع إلى قوة تحاول إرجاعه إلى الوضع التوازني وتكون متناسبة مع إزاحته s، فإذا رمزنا لثابت التناسب بـ ′k تكون هذه القوة مساوية وتتحدد هذه القوة بمعرفة المادة. عند دراسة تحريك الإلكترون نضيفها إلى القوة الكهربائية q حيث q شحنة الإلكترون ويمثل في هذه الحالة الحقل المحلّي بما فيه الحقل الناتج عن الجسيمات المجاورة. تقوم الذرات بصورة عامة بحركة اهتزازية ميكانيكية تتأثر بالقوى الكهربائية فيتحول جزء من الطاقة الكهربائية إلى طاقة ميكانيكية ويكون هذا ممثلاً بقوة متناسبة مع السرعة بما يشبه قوة الاحتكاك نكتبها على الصورة لتصير معادلة التحريك على الصورة:

ملف:3120-16.jpg

فإذا طُبق حقل ثم رُفع تأثير الحقل تماماً. يكون الطرف الأيمن من المعادلة معدوماً. وإذا افترض عدم وجود قوة احتكاك مبددّة أي أن الحد الثاني من المعادلة معدوم أيضاً عندئذ يكون حل المعادلة من الشكل:

ملف:3120-17.jpg

حيث الذي يعرف بالتواتر الزاوي الخاص للإلكترون، فهو يحوي خاصة من خواص الجسيم المدروس m وخاصة من خواص المادة ′k .

أما إذا طبقنا حقلاً كهربائياً مهتزاً بتواتر زاوي w أن نكتب في الطرف الأيمن . عندئذ، يمكن إيجاد حل للمعادلة من الشكل

ملف:3120-20.jpg

حيث φ ما يعرف بزاوية الطور، شريطة أن يحقق S العلاقة التالية:

ملف:3120-21.jpg

يلاحظ حدوث التجاوب المقابل لقيم كبيرة جداً لـ S عندما w=wo. إن وجود الحد الثاني المقابل للاحتكاك يمنع وصول S إلى قيم لانهائية وعند إدخال هذا الحد نحصل على الحل العام التالي:

ملف:3120-22.jpg

حيث j هو العدد التخيلي. يربط الآن بين السلوك الفردي على المستوى الذري مع السلوك الجهري macroscopic لنصل إلى ε ومنها إلى n. إن عزم ثنائي القطب هو qS والذي منه يمكن أن نعرف الاستقطابية الالكترونية ثم ما يقابل الاستقطابية α′=Nα حيث N العدد في واحدة الحجم فنجد أن:

ملف:3120-25.jpg

يظهر من هذه العلاقة أن n2 هو عدد عقدي له جزءان الأول له علاقة بسرعة الانتشار والثاني تخيلي له علاقة بالامتصاص وذلك عند حساب الطاقة الضائعة أو المبدّدة. ويظهر الشكل 2 سلوك الجزء الحقيقي الذي يكون هو المقصود عادة بقرينة الانكسار الممثلة لتغير سرعة الانتشار في حالتين: عدم وجود امتصاص (الخط المتقطع) ومع وجود امتصاص (الخط المستمر) وذلك عندما يتغير التواتر الزاوي w للحقل المطبق، ويتركز السلوك الغريب بجوار التواتر w0 الذي يقابله في الجزء التخيلي قيمة عالية جداً أي امتصاص شديد.

ملف:تغير قرينة الانكسار بتغير التواتر.jpg

ويتضح من هذا الشكل أن n2 وبالتالي n تزداد عند الاقتراب من يسار w0 مع ازدياد w تناقص حتى تكون w = w1 ويحدث الأمر ذاته بدءاً من w = w2 إلى ما لا نهاية. لكن الوضع مختلف ما بين التواترين w1 و w2 حيث تتناقص n مع تزايد w وهذا مايعرف بالتبدد الشاذ تمييزاً له عن الحالة الطبيعية الأولى. وبعيداً عن w0 ومع غياب الامتصاص يكون السلوك مشابهاً لعلاقة كوشي المذكورة سابقاً.

إن المعالجة السابقة نصف تقليدية لكنها تُظهر السِّمات الرئيسية إذ لا بد عند دراسة الذرات وإلكتروناتها أو الجزيئات من استخدام ميكانيك الكم للوصول إلى خواصها المجهرية. بيد أن الدراسة وفق ميكانيك الكم تقود إلى علاقة مماثلة بين n و ε والتواتر w لكنها تدخل تواترات خاصة عديدة wi مكان التواتر الخاص المميز w0 ويشير الدليل i إلى عددها سواء في الذرة أو في الجزيئة وتقابل هذه التواترات انتقالات ممكنة بين مستويات طاقتها، كما يدخل لكل انتقال شدة اهتزازية fi تقابل احتمال حدوث هذا الانتقال، فاحتمالات الانتقال بين سويات مختلفة ليست متساوية ويكون للجسيم المدروس كتلة mi وشحنته qi، وبالتالي فإن الانتقالات والتجاوبات المقابلة تصبح عديدة تختلف باختلاف الجسيم وبالتالي ما يتبعه من استقطابية فلدينا استقطابية إلكترونية في الحالة المدرروسة والاستقطابية الأيونية في حالة دراستنا للأيونات وغالباً ما تكون التواترات التجاوبية المقابلة متباعدة. وتعمم العلاقة لتصبح:

ملف:3120-26.jpg

وإن ما يهمنا من هذه التواترات التواترات الواقعة في المجال المرئي لإنها تؤثر تأثيراً كبيراً على سلوك هذه المواد على ضوئها، وقد تكون متقاربة فيتغير شكل المنحني تغيرات يمكن أن توصف بتراكب سلوك مجموعة من المنحنيات المشابهة.

يظهر في بعض البلورات اتجاهات استقطاب ذاتية تقابل اصطفاف الأيونات أو الجزيئات المكونة لها، التي تمثل ثنائيات أقطاب دائمة، في اتجاه مفضل عندئذ يختلف سلوك الضوء من حيث اتجاه سرعة الانتشار وقيمتها باختلاف اتجاه استقطاب هذا الضوء أي باختلاف متجهة حقله الكهربائي بالنسبة لهذا الاتجاه المفضل الذي يدعى المحور الضوئي، فيختلف تبعاً لذلك عامل الامتصاص وقرينة الانكسار باختلاف الاتجاه.

يشار أخيراً إلى أن الدراسة السابقة قد ركّزت على إلكترون أو أيون مرتبط، وبالتالي وجود قوة تحاول إعادته، غير أنه يمكن الحديث عن مجموعة من الشحنات السالبة مرتبطة ارتباطاً جماعياً بأيونات موجبة شبه ثابتة في مواقعها كما في حالة المعادن فهناك إلكترونات شبه حرة تستجيب للحقل الكهربائي استجابة جماعية كالأمواج وتعامل العينة ككل معاملة جزيئة كبيرة ينزاح مركز شحناتها السالب عن مركز شحناتها الموجب ويظهر تواتر مميز لهذه الحركة يتعلق بعدد الشحنات في واحدة الحجم N وكتلتها العطالية m* ضمن المعدن التي تختلف عادة عن كتلتها في الخلاء يدعى هذا بتواتر البلازما wp المعطى بالعلاقة:

ملف:3120-27.jpg

ويختلف سلوك المعدن عند تغير تواتر الضوء المتفاعل معه اختلافاً واضحاً تبعاً لكون تواتر الضوء أعلى أو أخفض من هذا التواتر. وهناك بعض أنصاف النواقل التي تحتوي شحنات حرة بتراكيز مناسبة لتظهر تأثيراتها على الضوء الساقط عليها ويمكن أن تكون الشحنات الحرة فيها موجبة الإشارة أو سالبة اصطلاحياً.

 أمثلة للتشتت

The most familiar example of dispersion is probably a rainbow, in which dispersion causes the spatial separation of a white light into components of different wavelengths (different colors). However, dispersion also has an effect in many other circumstances: for example, group-velocity dispersion causes pulses to spread in optical fibers, degrading signals over long distances; also, a cancellation between group-velocity dispersion and nonlinear effects leads to soliton waves.

 تشتت المواد والأدلة الموجية

Most often, chromatic dispersion refers to bulk material dispersion, that is, the change in refractive index with optical frequency. However, in a waveguide there is also the phenomenon of waveguide dispersion, in which case a wave's phase velocity in a structure depends on its frequency simply due to the structure's geometry. More generally, "waveguide" dispersion can occur for waves propagating through any inhomogeneous structure (e.g., a photonic crystal), whether or not the waves are confined to some region.^{[محل شك]} In a waveguide, both types of dispersion will generally be present, although they are not strictly additive. For example, in fiber optics the material and waveguide dispersion can effectively cancel each other out to produce a zero-dispersion wavelength, important for fast fiber-optic communication.

 تشتت المواد في علم البصريات

The variation of refractive index vs. vacuum wavelength for various glasses. The wavelengths of visible light are shaded in grey.

Influences of selected glass component additions on the mean dispersion of a specific base glass (n_F valid for λ = 486 nm (blue), n_C valid for λ = 656 nm (red))

Material dispersion can be a desirable or undesirable effect in optical applications. The dispersion of light by glass prisms is used to construct spectrometers and spectroradiometers. However, in lenses, dispersion causes chromatic aberration, an undesired effect that may degrade images in microscopes, telescopes, and photographic objectives.

The phase velocity v of a wave in a given uniform medium is given by

${\displaystyle{\displaystyle v={\frac{c}{n}},}}$

where c is the speed of light in vacuum, and n is the refractive index of the medium.

In general, the refractive index is some function of the frequency f of the light, thus n = n(f), or alternatively, with respect to the wave's wavelength n = n(λ). The wavelength dependence of a material's refractive index is usually quantified by its Abbe number or its coefficients in an empirical formula such as the Cauchy or Sellmeier equations.

Because of the Kramers–Kronig relations, the wavelength dependence of the real part of the refractive index is related to the material absorption, described by the imaginary part of the refractive index (also called the extinction coefficient). In particular, for non-magnetic materials (μ = μ₀), the susceptibility χ that appears in the Kramers–Kronig relations is the electric susceptibility χ_e = n² − 1.

The most commonly seen consequence of dispersion in optics is the separation of white light into a color spectrum by a prism. From Snell's law it can be seen that the angle of refraction of light in a prism depends on the refractive index of the prism material. Since that refractive index varies with wavelength, it follows that the angle that the light is refracted by will also vary with wavelength, causing an angular separation of the colors known as angular dispersion.

For visible light, refraction indices n of most transparent materials (e.g., air, glasses) decrease with increasing wavelength λ:

${\displaystyle{\displaystyle 1<n(\lambda_{\text{red}})<n(\lambda_{\text{yellow}})<n(\lambda_{\text{blue}}),}}$

or generally,

${\displaystyle{\displaystyle{\frac{dn}{d\lambda}}<0.}}$

In this case, the medium is said to have normal dispersion. Whereas if the index increases with increasing wavelength (which is typically the case in the ultraviolet), the medium is said to have anomalous dispersion.

At the interface of such a material with air or vacuum (index of ~1), Snell's law predicts that light incident at an angle θ to the normal will be refracted at an angle arcsin(sin θ/n). Thus, blue light, with a higher refractive index, will be bent more strongly than red light, resulting in the well-known rainbow pattern.

 تشتت سرعة المجموعة

المقالة الرئيسية: Group-velocity dispersion

Time evolution of a short pulse in a hypothetical dispersive medium (k = ω²) showing that the longer-wavelength components travel faster than the shorter-wavelength components (positive GVD), resulting in chirping and pulse broadening

Beyond simply describing a change in the phase velocity over wavelength, a more serious consequence of dispersion in many applications is termed group-velocity dispersion (GVD). While phase velocity v is defined as v = c/n, this describes only one frequency component. When different frequency components are combined, as when considering a signal or a pulse, one is often more interested in the group velocity, which describes the speed at which a pulse or information superimposed on a wave (modulation) propagates. In the accompanying animation, it can be seen that the wave itself (orange-brown) travels at a phase velocity much faster than the speed of the envelope (black), which corresponds to the group velocity. This pulse might be a communications signal, for instance, and its information only travels at the group velocity rate, even though it consists of wavefronts advancing at a faster rate (the phase velocity).

It is possible to calculate the group velocity from the refractive-index curve n(ω) or more directly from the wavenumber k = ωn/c, where ω is the radian frequency ω = 2πf. Whereas one expression for the phase velocity is v_p = ω/k, the group velocity can be expressed using the derivative: v_g = dω/dk. Or in terms of the phase velocity v_p,

${\displaystyle{\displaystyle v_{\text{g}}={\frac{v_{\text{p}}}{1-{\dfrac{\omega}{v_{\text{p}}}}{\dfrac{dv_{\text{p}}}{d\omega}}}}.}}$

When dispersion is present, not only the group velocity is not equal to the phase velocity, but generally it itself varies with wavelength. This is known as group-velocity dispersion and causes a short pulse of light to be broadened, as the different-frequency components within the pulse travel at different velocities. Group-velocity dispersion is quantified as the derivative of the reciprocal of the group velocity with respect to angular frequency, which results in group-velocity dispersion = d²k/dω².

If a light pulse is propagated through a material with positive group-velocity dispersion, then the shorter-wavelength components travel slower than the longer-wavelength components. The pulse therefore becomes positively chirped, or up-chirped, increasing in frequency with time. On the other hand, if a pulse travels through a material with negative group-velocity dispersion, shorter-wavelength components travel faster than the longer ones, and the pulse becomes negatively chirped, or down-chirped, decreasing in frequency with time.

An everyday example of a negatively chirped signal in the acoustic domain is that of an approaching train hitting deformities on a welded track. The sound caused by the train itself is impulsive and travels much faster in the metal tracks than in air, so that the train can be heard well before it arrives. However, from afar it is not heard as causing impulses, but leads to a distinctive descending chirp, amidst reverberation caused by the complexity of the vibrational modes of the track. Group-velocity dispersion can be heard in that the volume of the sounds stays audible for a surprisingly long time, up to several seconds.

 التحكم في التشتت

The result of GVD, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fiber, since if dispersion is too high, a group of pulses representing a bit-stream will spread in time and merge, rendering the bit-stream unintelligible. This limits the length of fiber that a signal can be sent down without regeneration. One possible answer to this problem is to send signals down the optical fibre at a wavelength where the GVD is zero (e.g., around 1.3–1.5 μm in silica fibres), so pulses at this wavelength suffer minimal spreading from dispersion. In practice, however, this approach causes more problems than it solves because zero GVD unacceptably amplifies other nonlinear effects (such as four-wave mixing). Another possible option is to use soliton pulses in the regime of negative dispersion, a form of optical pulse which uses a nonlinear optical effect to self-maintain its shape. Solitons have the practical problem, however, that they require a certain power level to be maintained in the pulse for the nonlinear effect to be of the correct strength. Instead, the solution that is currently used in practice is to perform dispersion compensation, typically by matching the fiber with another fiber of opposite-sign dispersion so that the dispersion effects cancel; such compensation is ultimately limited by nonlinear effects such as self-phase modulation, which interact with dispersion to make it very difficult to undo.

Dispersion control is also important in lasers that produce short pulses. The overall dispersion of the optical resonator is a major factor in determining the duration of the pulses emitted by the laser. A pair of prisms can be arranged to produce net negative dispersion, which can be used to balance the usually positive dispersion of the laser medium. Diffraction gratings can also be used to produce dispersive effects; these are often used in high-power laser amplifier systems. Recently, an alternative to prisms and gratings has been developed: chirped mirrors. These dielectric mirrors are coated so that different wavelengths have different penetration lengths, and therefore different group delays. The coating layers can be tailored to achieve a net negative dispersion.

 في الأدلة الموجية

Waveguides are highly dispersive due to their geometry (rather than just to their material composition). Optical fibers are a sort of waveguide for optical frequencies (light) widely used in modern telecommunications systems. The rate at which data can be transported on a single fiber is limited by pulse broadening due to chromatic dispersion among other phenomena.

In general, for a waveguide mode with an angular frequency ω(β) at a propagation constant β (so that the electromagnetic fields in the propagation direction z oscillate proportional to e^i(βz−ωt)), the group-velocity dispersion parameter D is defined as

${\displaystyle{\displaystyle D=-{\frac{2\pi c}{\lambda^{2}}}{\frac{d^{2}\beta}{d\omega^{2}}}={\frac{2\pi c}{v_{g}^{2}\lambda^{2}}}{\frac{dv_{g}}{d\omega}},}}$

where λ = 2πc/ω is the vacuum wavelength, and v_g = dω/dβ is the group velocity. This formula generalizes the one in the previous section for homogeneous media and includes both waveguide dispersion and material dispersion. The reason for defining the dispersion in this way is that |D| is the (asymptotic) temporal pulse spreading Δt per unit bandwidth Δλ per unit distance travelled, commonly reported in ps/(nm⋅km) for optical fibers.

In the case of multi-mode optical fibers, so-called modal dispersion will also lead to pulse broadening. Even in single-mode fibers, pulse broadening can occur as a result of polarization mode dispersion (since there are still two polarization modes). These are not examples of chromatic dispersion, as they are not dependent on the wavelength or bandwidth of the pulses propagated.

 التشتت من درجةٍ أعلى على نطاق واسع

When a broad range of frequencies (a broad bandwidth) is present in a single wavepacket, such as in an ultrashort pulse or a chirped pulse or other forms of spread spectrum transmission, it may not be accurate to approximate the dispersion by a constant over the entire bandwidth, and more complex calculations are required to compute effects such as pulse spreading.

In particular, the dispersion parameter D defined above is obtained from only one derivative of the group velocity. Higher derivatives are known as higher-order dispersion. These terms are simply a Taylor series expansion of the dispersion relation β(ω) of the medium or waveguide around some particular frequency. Their effects can be computed via numerical evaluation of Fourier transforms of the waveform, via integration of higher-order slowly varying envelope approximations, by a split-step method (which can use the exact dispersion relation rather than a Taylor series), or by direct simulation of the full Maxwell's equations rather than an approximate envelope equation.

 التشتت الفراغي

المقالة الرئيسية: تشتت فراغي

In electromagnetics and optics, the term dispersion generally refers to aforementioned temporal or frequency dispersion. Spatial dispersion refers to the non-local response of the medium to the space; this can be reworded as the wavevector dependence of the permittivity. For an exemplary anisotropic medium, the spatial relation between electric and electric displacement field can be expressed as a convolution:

${\displaystyle{\displaystyle D_{i}(t,r)=E_{i}(t,r)+\int_{0}^{\infty}\int f_{ik}(\tau;r,r^{\prime})E_{k}(t-\tau,r^{\prime})\,dV^{\prime}\,d\tau,}}$

where the kernel ${\displaystyle{\displaystyle f_{ik}}}$ is dielectric response (susceptibility); its indices make it in general a tensor to account for the anisotropy of the medium. Spatial dispersion is negligible in most macroscopic cases, where the scale of variation of ${\displaystyle{\displaystyle E_{k}(t-\tau,r^{\prime})}}$ is much larger than atomic dimensions, because the dielectric kernel dies out at macroscopic distances. Nevertheless, it can result in non-negligible macroscopic effects, particularly in conducting media such as metals, electrolytes and plasmas. Spatial dispersion also plays role in optical activity and Doppler broadening, as well as in the theory of metamaterials.

 التشتت في علم الجواهر

قيم التشتت للمعادن أظهر

Mineral name	nB − nG	nC − nF
Hematite	0.500	—
Cinnabar (HgS)	0.40	—
synth. Rutile	0.330	0.190
Rutile (TiO2)	0.280	0.120–0.180
Anatase (TiO2)	0.213–0.259	—
Wulfenite	0.203	0.133
Vanadinite	0.202	—
Fabulite	0.190	0.109
Sphalerite (ZnS)	0.156	0.088
Sulfur (S)	0.155	—
Stibiotantalite	0.146	—
Goethite (FeO(OH))	0.14	—
Brookite (TiO2)	0.131	0.12–1.80
Linobate	0.13	0.075
Zincite (ZnO)	0.127	—
synth. Moissanite (SiC)	0.104	—
Cassiterite (SnO2)	0.071	0.035
Zirconia (ZrO2)	0.060	0.035
Powellite (CaMoO4)	0.058	—
Andradite	0.057	—
Demantoid	0.057	0.034
Cerussite	0.055	0.033–0.050
Titanite	0.051	0.019–0.038
Benitoite	0.046	0.026
Anglesite	0.044	0.025
Diamond (C)	0.044	0.025
synth. Cassiterite (SnO2)	0.041	—
Flint glass	0.041	—
Hyacinth	0.039	—
Jargoon	0.039	—
Starlite	0.039	—
Scheelite	0.038	0.026
Zircon (ZrSiO4)	0.039	0.022
GGG	0.038	0.022
Dioptase	0.036	0.021
Whe Vinay wellite	0.034	—
Gypsum	0.033	0.008
Alabaster	0.033	—
Epidote	0.03	0.012–0.027
Tanzanite	0.030	0.011
Thulite	0.03	0.011
Zoisite	0.03	—
YAG	0.028	0.015
Spessartine	0.027	0.015
Uvarovite	0.027	0.014–0.021
Almandine	0.027	0.013–0.016
Hessonite	0.027	0.013–0.015
Willemite	0.027	—
Pleonaste	0.026	—
Rhodolite	0.026	—
Boracite	0.024	0.012
Cryolite	0.024	—
Staurolite	0.023	0.012–0.013
Pyrope	0.022	0.013–0.016
Diaspore	0.02	—
Grossular	0.020	0.012
Hemimorphite	0.020	0.013
Kyanite	0.020	0.011
Peridot	0.020	0.012–0.013
Spinel	0.020	0.011
Vesuvianite	0.019–0.025	0.014
Gahnite	0.019–0.021	—
Clinozoisite	0.019	0.011–0.014
Labradorite	0.019	0.010
Axinite	0.018–0.020	0.011
Diopside	0.018–0.020	0.01
Ekanite	0.018	0.012
Corundum (Al2O3)	0.018	0.011
synth. Corundum	0.018	0.011
Ruby (Al2O3)	0.018	0.011
Sapphire (Al2O3)	0.018	0.011
Kornerupine	0.018	0.010
Sinhalite	0.018	0.010
Sodalite	0.018	0.009
Rhodizite	0.018	—
Hiddenite	0.017	0.010
Kunzite	0.017	0.010
Spodumene	0.017	0.010
Tourmaline	0.017	0.009–0.011
Cordierite	0.017	0.009
Danburite	0.017	0.009
Herderite	0.017	0.008–0.009
Rubellite	0.017	0.008–0.009
Achroite	0.017	—
Dravite	0.017	—
Elbaite	0.017	—
Indicolite	0.017	—
Liddicoatite	0.017	—
Scapolite	0.017	—
Schorl	0.017	—
Verdelite	0.017	—
Andalusite	0.016	0.009
Baryte (BaSO4)	0.016	0.009
Euclase	0.016	0.009
Datolite	0.016	—
Alexandrite	0.015	0.011
Chrysoberyl	0.015	0.011
Rhodochrosite	0.015	0.010–0.020
Sillimanite	0.015	0.009–0.012
Hambergite	0.015	0.009–0.010
Pyroxmangite	0.015	—
synth. Scheelite	0.015	—
Smithsonite	0.014–0.031	0.008–0.017
Amblygonite	0.014–0.015	0.008
Aquamarine	0.014	0.009–0.013
Beryl	0.014	0.009–0.013
Emerald	0.014	0.009–0.013
Heliodor	0.014	0.009–0.013
Morganite	0.014	0.009–0.013
Brazilianite	0.014	0.008
Celestine	0.014	0.008
Topaz	0.014	0.008
Goshenite	0.014	—
Apatite	0.013	0.008–0.010
Aventurine	0.013	0.008
Amethyst (SiO2)	0.013	0.008
Citrine quartz	0.013	0.008
Prasiolite	0.013	0.008
Quartz (SiO2)	0.013	0.008
Rose quartz (SiO2)	0.013	0.008
Smoky quartz (SiO2)	0.013	0.008
Anhydrite	0.013	—
Dolomite	0.013	—
Morion	0.013	—
Feldspar	0.012	0.008
Moonstone	0.012	0.008
Orthoclase	0.012	0.008
Pollucite	0.012	0.007
Albite	0.012	—
Bytownite	0.012	—
synth. Emerald	0.012	—
Magnesite (MgCO3)	0.012	—
Sanidine	0.012	—
Sunstone	0.012	—
synth. Alexandrite	0.011	—
synth. Sapphire (Al2O3)	0.011	—
Phosphophyllite	0.010–0.011	—
Phenakite	0.01	0.009
Cancrinite	0.010	0.008–0.009
Leucite	0.010	0.008
Enstatite	0.010	—
Obsidian	0.010	—
Anorthite	0.009–0.010	—
Actinolite	0.009	—
Jeremejevite	0.009	—
Nepheline	0.008–0.009	—
Apophyllite	0.008	—
Hauyne	0.008	—
Natrolite	0.008	—
synth. Quartz (SiO2)	0.008	—
Aragonite	0.007–0.012	—
Augelite	0.007	—
Beryllonite	0.010	0.007
Strontianite	0.008–0.028	—
Calcite (CaCO3)	0.008–0.017	0.013–0.014
Fluorite (CaF2)	0.007	0.004
Tremolite	0.006–0.007	—

In the technical terminology of gemology, dispersion is the difference in the refractive index of a material at the B and G (686.7 nm and 430.8 nm) or C and F (656.3 nm and 486.1 nm) Fraunhofer wavelengths, and is meant to express the degree to which a prism cut from the gemstone demonstrates "fire". Fire is a colloquial term used by gemologists to describe a gemstone's dispersive nature or lack thereof. Dispersion is a material property. The amount of fire demonstrated by a given gemstone is a function of the gemstone's facet angles, the polish quality, the lighting environment, the material's refractive index, the saturation of color, and the orientation of the viewer relative to the gemstone.

 التشتت في مجال التصوير

In photographic and microscopic lenses, dispersion causes chromatic aberration, which causes the different colors in the image not to overlap properly. Various techniques have been developed to counteract this, such as the use of achromats, multielement lenses with glasses of different dispersion. They are constructed in such a way that the chromatic aberrations of the different parts cancel out.

 انبعاثات النباضات

Pulsars are spinning neutron stars that emit pulses at very regular intervals ranging from milliseconds to seconds. Astronomers believe that the pulses are emitted simultaneously over a wide range of frequencies. However, as observed on Earth, the components of each pulse emitted at higher radio frequencies arrive before those emitted at lower frequencies. This dispersion occurs because of the ionized component of the interstellar medium, mainly the free electrons, which make the group velocity frequency-dependent. The extra delay added at a frequency ν is

${\displaystyle{\displaystyle t=k_{\text{DM}}\cdot\left({\frac{\text{DM}}{\nu^{2}}}\right),}}$

where the dispersion constant k_DM is given by

${\displaystyle{\displaystyle k_{\text{DM}}={\frac{e^{2}}{2\pi m_{\text{e}}c}}\approx 4.149~{}{\text{GHz}}^{2}\,{\text{pc}}^{-1}\,{\text{cm}}^{3}\,{\text{ms}},}}$

and the dispersion measure (DM) is the column density of free electrons (total electron content) – i.e. the number density of electrons n_e integrated along the path traveled by the photon from the pulsar to the Earth – and is given by

${\displaystyle{\displaystyle{\text{DM}}=\int_{0}^{d}n_{e}\,dl}}$

with units of parsecs per cubic centimetre (1 pc/cm³ = 30.857×10²¹ m⁻²).

Typically for astronomical observations, this delay cannot be measured directly, since the emission time is unknown. What can be measured is the difference in arrival times at two different frequencies. The delay Δt between a high-frequency ν_hi and a low-frequency ν_lo component of a pulse will be

${\displaystyle{\displaystyle\Delta t=k_{\text{DM}}\cdot{\text{DM}}\cdot\left({\frac{1}{\nu_{\text{lo}}^{2}}}-{\frac{1}{\nu_{\text{hi}}^{2}}}\right).}}$

Rewriting the above equation in terms of Δt allows one to determine the DM by measuring pulse arrival times at multiple frequencies. This in turn can be used to study the interstellar medium, as well as allow observations of pulsars at different frequencies to be combined.

 انظر أيضاً

• Calculation of glass properties incl. dispersion
• Cauchy's equation
• Dispersion relation
• Fast radio burst (astronomy)
• Fluctuation theorem
• Green–Kubo relations
• Group delay
• Intramodal dispersion
• Kramers–Kronig relations
• Linear response function
• Multiple-prism dispersion theory
• Sellmeier equation
• Ultrashort pulse
• Virtually imaged phased array

 وصلات خارجية

• Optical Characteristics of the SF10 Crystal Prism
• Deviation Angle for a Prism
• Dispersive Wiki - discussing the mathematical aspects of dispersion.
• Dispersion - Encyclopedia of Laser Physics and Technology