حث

كهرومغناطيسية

كهرباء • مغناطيسية كهروستاتيكية  · شحنة كهربائية · قانون كولوم · مجال كهربائي · تدفق كهربائي · قانون گاوس · كمون كهربائي · حث كهروستاتيكي · عزم ثنائي القطب كهربائي · استاتيكا مغناطيسية  · قانون أمبير · تيار كهربائي  · مجال مغناطيسي · تدفق مغناطيسي · قانون بيو-ساڤار · عزم مغناطيسي · قانون گاوس للمغناطيسية · ديناميكا كهربائية  · Free space · قانون قوة لورنتس · قوة محركة كهربائية · حث كهرومغناطيسي · قانون فاراداي · قانون لنز · تيار الإزاحة · معادلات ماكسويل · مجال كهرومغناطيسي · إشعاع كهرومغناطيسي · Liénard-Wiechert Potentials · Maxwell tensor · تيار دوامي · شبكة كهربائية  · توصيل كهربائي · مقاومة كهربائية · سعة كهربية · حث كهربي · معاوقة · فجوات رنانة · مرشد الموجة · Covariant formulation  · Electromagnetic tensor · EM Stress-energy tensor · Four-current · Four-potential · العلماء  · أمپير · كولوم · فاراداي · هيڤيسايد · هنري · هرتز · لورنتس · ماكسويل · تسلا · وبر · · غيرهم

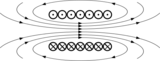
في الكهرومغناطيسية والإلكترونيات، الحث هو قدرة الناقل على تخزين الطاقة في المجال المغناطيسي.

التحريض أو المحاثة إنگليزية: electric inductance هي خاصية للدارة الكهربائية تعمل على مقاومة أي تغير في التيار الكهربائي نتيجة للمجال المغناطيسي المصاحب للتيار، فكلما تغيرت قيمة التيار الكهربائي زيادة أو نقصان في الدائرة يتغير مجاله المغناطيسي المصاحب له فتنتج في الموصل نفسه بالحث قوة دافعة كهربائية تحاول مقاومة التغيير الأصلي في التيار، وتسمى المحاثة الداخلية.

وحدة قياس المحاثة هي هنري.

عندما يحث تيار يتغير بمعدل أمبير واحد في الثانية، جهداً بالحث مقداره فولت واحد، فإن محاثة الدائرة الكهربائية تكون هنري واحد.

وتنشأ ظاهرة الحث أو التحريض حين يتحرك ناقل (موصل) في حقل مغنطيسي ساكن، أو حين يوضع ناقل في حقل مغنطيسي متغير؛ وتتجلى بظهور قوة محركة كهربائية (ق.م.ك) تحريضية، أي فرق في الكمون بين طرفي الناقل.

ويعود الفضل في كشف ظاهرة التحريض الكهرمغنطيسي إلى كل من مايكل فارادي Michael Faraday عام 1831 في إنكلترة، وجوسف هنري Joseph Henry في العام نفسه في الولايات المتحدة.

يبين الشكل بأجزائه المختلفة توضيحاً لبعض التجارب الأولية البسيطة التي تلقي الضوء على ظاهرة التحريض الكهرمغنطيسي وعلى ظهور القوة المحركة الكهربائية التحريضية. ففي الجزء (آ) يدل المقياس الغلفاني على مرور تيار متحرض في الوشيعة الساكنة في أثناء حركة المغنطيس. وفي الجزء (ب) تتكرر الظاهرة نفسها لدى استبدال دارة كهربائية يمر فيها تيار بالمغنطيس السابق. أما الجزء (جـ) فيبين أن الدارة المحرِّضة ساكنة بيد أنه يمكن تغيير التيار المار فيها عن طريق فتح قاطعة أو غلقها، أو تغيير شدة التيار فيها بوساطة مقاومة متغيرة (معدِّلة). إن الشيء المشترك في تلك التجارب التي يبينها الشكل (1) هو تغير الحقل المغنطيسي الذي يجتاز الدارة المتحرِّضة، ومن ثم تغير التدفق المغنطيسي الذي يجتازها.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 القوة المحركة الكهربائية الحركية

شكل يوضح حركة الناقل C في حقل مغنطيسي منتظم تحريضه ويتحرك بسرعة ثابتة (السهم فوق الحرف يعني أنه متجهة).

إن كل إلكترون يحمل شحنة سالبة e في الناقل يخضع لقوة مغنطيسية عمودية على كل من و وتكون جهتها بحيث تدفع الإلكترون باتجاه طرف الناقل عند A. وهكذا تتحرك الإلكترونات الحرة في الناقل متجمعة عند A فتتكون شحنة إضافية سالبة عند A وأخرى موجبة عند B فينشأ حقل كهربائي يتجه من B إلى A وهو يطبق قوةً كهربائية على الإلكترون وتتجه هذه القوة من A إلى B أي بعكس اتجاه القوة المغنطيسية. وتستمر عملية انتقال الشحنات الموجبة والسالبة كما يستمر تراكمها عند الطرفين A وB من الناقل، ومن ثم يزداد نمو الحقل إلى أن يغدو قادراً على وقف حركة الشحنات، وبذلك تتساوى القوة الكهربائية e والقوة المغنطيسية في القيمة وتتعاكسان في الجهة فتفني إحداهما الأخرى، وتصل الشحنات إلى حالة التوازن التي يكون عندها كمون طرف الناقل عند A أعلى من كمون طرفه عند B. ويحسب فرق الكمون بين طرفي الناقل A وB، ومن ثم فإن (ق.م.ك)ε المتحرضة بينهما من التكامل الخطي لفرق الكمون العنصري dv بين طرفي عنصر صغير منه dl يقع عند النقطة M والذي يمثل تجول الحقل الكهربائي بين هاتين النقطتين. وتستخدم في كثير من التطبيقات أجسام ناقلة كبيرة الحجم (ليست سلكية) تُجعل في حقل مغنطيسي متغير أو تتحرك في حقل مغنطيسي ثابت كما في الشكل (3). إن تجول بين نقطتين A وB من الناقل يختلف باختلاف الطريق الواصل بينهما (الجزء آ من الشكل 3). كما أن القوتين المحركتين الكهربائيتين ε1 وε2 الموافقتين للطريقين مختلفتان، ومن ثم فإن (ق.م.ك) المحصلة في العروة لا تكون معدومة مما يؤدي إلى مرور تيار كهربائي فيها. وتدور هذه التيارات المتحرضة في جسم الناقل وتدعى بالتيارات الدوارة Eddy currents بسبب طبيعتها، وتعرف باسم تيارات فوكو Foucault نسبة إلى كاشفها وهي تيارات غير مرغوب فيها لأنها تسخن الناقل وتسبب ضياعاً للطاقة. بيد أنه يمكن تخفيفها كثيراً بصنع الناقل على هيئة طبقات رقيقة منفصلة بعضها عن بعضها الآخر بعازل لزيادة المقاومة وانقاص التيار إلى حد كبير.

 قانون الحث لفارادي

ينص قانون فاراداي في التحريض على أن (ق.م.ك) المتحرضة ε في دارة تساوي معدل تغير التدفق f الذي يجتاز الدارة وتعاكسه في الإشارة. ويعبر عن هذا القانون بالمعادلة:

 النواقل المقترنة

للمزيد من المعلومات: اقتران (كهرباء)

مخطط لدارة كهربية يوضح النواقل المقترنة تناوبيا.

 الحقول الكهربائية المتحرضة

إذا كانت النواقل ساكنة في مواضعها، فلا شك في أن التغير في التدفق المغنطيسي الذي يجتاز الناقل يمكن أن يسببه حقل مغنطيسي متغير. ولا بد من استنتاج أن التيار المتحرض في الوشيعة يسببه حقل كهربائي متحرض. إن مثل هذا الحقل لا تولده شحنة كهربائية بل يولده الحقل المغنطيسي المتغير. وهو يختلف عن الحقل الكهربائي الناتج عن شحنات كهربائية ساكنة، ولتأكيد الاختلاف بين هذين الحقلين فقد جرت العادة على تسمية الحقل الكهربائي المتحرض بالحقل الكهربائي غير الساكن، ويرمز له بـ En. وإن الحقل الكهربائي المتحرض حقل غير محافظ لأن تكامله الخطي على طريق مغلق لا يساوي الصفر على عكس الحقل الكهراكدي.

 قانون لنْتز

تعيين جهة التيار المتحرض حسب قانون لنتز.

ينص قانون لنتز Lenz’s law على ما يأتي: «إن جهة (ق.م.ك) المتحرضة (أو التيار الناتج عنها) تعاكس السبب الذي أدى إلى حدوثها». وتشير إشارة الناقص في قانون فارادي إلى هذا التعاكس.

إذا كان «السبب» ناتجاً عن حركة المغنطيس. فإن الجزء (آ) منه يشير إلى زيادة التدفق في الوشيعة لذا يجب أن يتحرض فيها تيار i تكون جهته بحيث يكون وجه الوشيعة شمالياً N كما هو مبين في الشكل (4 ـ أ) وكذلك تعيَّن جهة التيار المتحرض لدى ابتعاد المغناطيس عن الوشيعة بحيث يكون وجه الوشيعة جنوبياً S كما هو مبين في الشكل (4 ـ ب).

وفي كل الأحوال ومهما يكن سبب تغير التدفق المغنطيسي في الوشيعة فإن جهة التيار المتحرض المار فيها تكون بحيث تؤدي إلى حقل مغنطيسي يعطي تدفقاً يعاكس التغير الذي طرأ على التدفق المحرِّض. ويعد قانون لِنتز صيغة أخرى لمبدأ انحفاظ الطاقة الذي يجب أن يبقى ساري المفعول في هذه الجملة. فاعتماداً على هذا المبدأ، يعني مرور التيار صرف طاقة كهربائية في دارة لا تحتوي على منبع للطاقة. وبما أن سبب التيار هو الحركة فإن هذه الطاقة يجب أن تكون معادلة للعمل المبذول من الوسيط الخارجي الذي يقوم بالحركة والذي يلاقي قوة تقاوم هذه الحركة. كمية الكهرباء المحرَّضة تؤدي كمية الكهرباء المحرّضة دوراً يشير إلى مجمل ما حدث. ويمكن أن تحسب بفرض أن للوشيعة التي يمر فيها التيار في الأشكال (1) أو (4) مقاومة غير مهملة تساوي R، فإن (ق.م.ك) المتحرضة فيها تولد تياراً i يعطى بالعلاقة:

ففي أثناء مدة قصيرة dt، تمر كمية من الكهرباء المحرَّضة dq:

فإذا استمر مرور التيار المتحرض مدة تحرضت كمية من الكهرباء:

حيث تمثل Δ f تغير التدفق في المدة الزمنية ما بين t1 و t2. وتشير المعادلة الأخيرة إلى أن قياس التغير في التدفق يعطي قياساً لكمية الكهرباء المحرَّضة في الدارة. وبالعكس، إذا قيست كمية الكهرباء أمكن قياس Δ f ومن ثم أمكن قياس حقل التحرض المغنطيسي الذي أحدثها. وهذه إحدى الطرائق المتبعة لقياس التحريض المغنطيسي .

 تقنيات الحساب

 الحث الذاتي

الحث الذاتي هو حالة خاصة من ظاهرة التحريض الكهرمغنطيسي، والفرق بينهما هو أنه في ظاهرة التحريض الكهرمغنطيسي يكون تَغيُّر التدفق[ر] (الفيْض flux) المغنطيسي، عبْر سطح الدارة التي يتحرض فيها التيار الكهربائي، ناجماً عن مصدرٍ خارجي بالنسبة إلى الدارة، أما في ظاهرة التحريض الذاتي فإنّ تَغَيّر التدفق المغنطيسي عبْر سطح الدارة ينشأ عن تغير شدة التيار الكهربائي الذي يجتاز الدارة نفسها. فمثلاً، المِلَفُّ المجتاز بتيار، يتلقى تدفقاً مغنطيسياً f يُولِّده هذا التيار نفسُه. فإذا تغيرت شدة التيار، أو تَشَوَّه شكل الملف، تَغيََّر التدفق f وصار الملف مُسْتَقَرَّ قوة محركة كهربائية(ق م ك) تحريضية ذاتية es، يعطي قانون فارادي شدتها، فهي تساوي بالقدر مشتق التدفق (بالنسبة إلى الزمن t. أما إشارة الناقص فتُعبّر عن قانون لنز Lenz الذي ينص على أن es تسعى لمعاكسةِ تَغيُّرِ التيار، أو لمعاكسةِ تَشَوُّهِ الملف.

 معامل الحث الذاتي

يمكن مقارنة التدفق f الذي تُولِّده وتتلقاه دارةٌ مّا، بشدة التيار الذي أدى إلى نشوئه. وتُحدِّد النسبةُ بينهما L، المسماةُ «مُحارَضَة» الدارة، أهمية التدفق الذي ترسله الدارةُ عبْر الدارة نفسِها، في حالة تيار معيَّن. إن المقدار L موجب دوماً، ويكون ثابتَ القيمة إذا كانت الدارة صلبةً (غير قابلة للتشوه) وموضوعةً في وَسَطٍ مغنطيسي ذي نفوذية (نفاذية permeability) ثابتة، ذلك لأن التدفق يتناسب عندئذ مع التيار. أما إذا كانت الدارة ليّنة (قابلة للتشوه) أو موضوعة في وسطٍ حديديّ التمغْنط ferromagnetic فإن L يكون متغيراً، وهذه حالة ملفٍ ذي نواة (قَلْبٍ core) حديدية.

تسمح العلاقة بين تغير شدة التيار والقوة المحركة الكهربائية الناتجة عنها تعريف وحدة قياس المحارضة في النظام (الجملة) الدولي SI للوحدات، وهي الهنري henri، ورمزها H، إذ تكون محارضة الدارة المغلقة مساوية 1H إذا تحرضت فيها ق م ك قدرها فُلْط واحد 1V عندما يتغير التيار الكهربائي الذي يجتازها تغيراً منتظماً بمعدل أمبير واحد 1A في الثانية. وهذا يكافئ القول: إن هذه الدارة تتلقى تدفقاً قدره فيبر واحد 1W عندما يجتازها تيار شدته أمبير واحد.

 تعيين قيم المحارضات

يمكن، في عدد من الحالات، حساب محارضة الملف انطلاقاً من شكله الهندسي وعدد لفّاته؛ وهناك كُتيّبات مخصصة لهذا الحساب؛ ويلاحظ فيها أن المحارضة تتناسب مع مربع عدد اللفات. فمثلاً، في حالة ملف بلا تَسَرُّبٍ مغنطيسي (وذلك عندما يتلقى جميعُ اللفّات خطوط تدفقٍ واحدة) تكون عبارة المحارضة: L = N2/R حيث N عدد اللفّات، وR هي الممانعة المغنطيسية reluctance التي تُبديها الدارة لمجموعة خطوط التدفق.

وفي معظم الحالات تُعيَّن المحارضة بالقياس. وثمة طرائق عديدة لتنفيذ ذلك، أهمها استعمال التجاوب resonance الكهربائي وجُسور المُعاوَقات impedance كجسر ويتسطن (الشكل-1). يستعمل هذا الجسر إذا كان الملف المراد قياس محارضته L عديم المقاومة الأومية r = 0. وهذا مستحيل عملياً، إنما يمكن أن تكون r صغيرة جداً إزاء Lw حيث w نبض التيار المتناوب الذي يغذي الجسر. وتُختار المقاومتان r1 و r2 بحيث ينعدم فرق الكمون(الجهد) بين طرفي الجسر E ، D ـ ومن ثّم ينعدم التيار في الكاشف الصِّفريّ T (سمّاعة هاتف مثلاً، فينعدم فيها الصوت أو تبلغ شدته حداً أدنى). ويقال عندئذ إن الجسر متوازن ـ وتتحقق آنئذ العلاقة L = C r1 r2 التي تعطي قيمة المحارضة المجهولة بدلالة سعة المكثفة C والمقاومتين r1 و r2.

أما إذا كانت مقاومة الملف r غير مهملة، فيُستعمل جسر مكسويل (الشكل-2)، الذي يختلف عن جسر ويتسطن بوصل مقاومة r1 على التفرع مع المكثفة. ولِتَوازن جسر مكسويل شرطان هما:

r1 r2 = r r1 = L /C ومن أحدهما تُحسب L.

وعند وصل مِلَفَّين على التسلسل تكون المحارضة الكلية مساوية:

L = L1 + L2 2M

حيث L1 و L2 محارضتا الملفين على الترتيب، وM معامل التحريض المتبادل، وتتوقف قيمته على الوضع النسبي للملفين. فإذا كان هذا الوضع قابلاً للتغيير أمكن الحصول على محارضة كلية متغيرة (قابلة للتعديل) تقع قيمتها بين: L1 + L2 + 2M و L1 + L2 2M

تأثير التحريض الذاتي عند إغلاق الدارة الكهربائية وفتحها

1 ـ إغلاق الدارة: إذا أغلقت دارةٌ، مقاومتها الكلية R ومحارضتها الثابتة L، على ق م ك مستمرة(متواصلة) قيمتها e(الشكل-3)، فإن شدة التيار تكون متغيرة، فلا تقفز الشدة فجأة من الصفر إلى القيمة النهائية I = e / R التي يقتضيها قانون أوم، وإنما تتغير، بَدءاً من لحظة الإغلاق t = 0، وفق منحن بياني (الشكل-4).

فالقوة المحركة الكهربائية التحريضية الذاتية تَوَطُّد التيار الذي يستغرق، نظرياً، زمناً لانهائياً ليبلغ قيمته النهائية I. وكلما صَغُر المقدار المسمى «الثابتة الزمنية» زادت سرعة اقتراب i من I لأن:

ففي اللحظة تكون النسبة i/I مساوية:

وفي اللحظة تكون النسبة i/I مساوية:

وفي اللحظة تكون النسبة i/I مساوية:

ويُستنتج الميزان الطاقيّ بالمكاملة فنجد: a = b + c

حيث يمثِل المقدار a الطاقة الكلية التي يقدمها المولد. ويمثل المقدار b الطاقة المتبددة بفعل جول. أما المقدار c فيمثل الطاقة الكهرمغنطيسية المختزنة في الملف.

2 ـ فَتْح الدارة: عند فتح الدارة يكوِّن مربطا القاطعة مكثفة بعيدة جداً من الكمال. وبسبب تلاشي التيار تتحول الطاقة الكهرمغنطيسية المختزنة إلى طاقة كهراكدية electrostatic . ويمكن أن تكون c، وهي سعة القاطعة، صغيرة جداً، ومن ثَم يمكن أن يصير فرق الكمون U بين مربطيها كبيراً فيُسبّب انقداح قوسٍ كهربائية تسمى «شرارة الانقطاع». ولهذه الظاهرة محاذير منها: انثقاب العوازل، وتَلَفُ مرابط القواطع، وخطر الانصعاق بالكهرباء، وإصدار موجات كهرمغنطيسية (تشويش الاتصالات الراديوية). ويمكن معالجة الأمر بوصل مكثفة كبيرة السعة إلى مربطي القاطعة، أو بوضع مقاومة على التفرع (التوازي) مع الملف في لحظة فتْح الدارة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 العلاقة بين الحث والسعة

تبين المعادلة التالية العلاقة بين الحث والسعة:

$\displaystyle L'C'={\varepsilon \mu }.$

 الحث الذاتي في الدارات الكهربية البسيطة في الهواء

الحث الذاتي في الدارات الكهربية البسيطة في الهواء

النوع	الحث/ $\mu _{0}$	تعليق
Single layer solenoid	${\frac {r^{2}N^{2}}{3l}}\left\{-8w+4{\frac {\sqrt {1+m}}{m}}\left(K\left({\sqrt {\frac {m}{1+m}}}\right)-\left(1-m\right)E\left({\sqrt {\frac {m}{1+m}}}\right)\right)\right\}$ $={\frac {r^{2}N^{2}\pi }{l}}\left\{1-{\frac {8w}{3\pi }}+\sum _{n=1}^{\infty }{\frac {\left(2n\right)!^{2}}{n!^{4}\left(n+1\right)\left(2n-1\right)2^{2n}}}\left(-1\right)^{n+1}w^{2n}\right\}$ $={\frac {r^{2}N^{2}\pi }{l}}\left(1-{\frac {8w}{3\pi }}+{\frac {w^{2}}{2}}-{\frac {w^{4}}{4}}+{\frac {5w^{6}}{16}}-{\frac {35w^{8}}{64}}+...\right)$ for w << 1 $=rN^{2}\left\{\left(1+{\frac {1}{32w^{2}}}+O({\frac {1}{w^{4}}})\right)\ln {8w}-1/2+{\frac {1}{128w^{2}}}+O({\frac {1}{w^{4}}})\right\}$ for w >> 1	$N$: Number of turns r: Radius l: Length w = r/l $m=4w^{2}$ $E,K$: Elliptic integrals
Coaxial cable, high frequency	${\frac {l}{2\pi }}\ln {\frac {a_{1}}{a}}$	a1: Outer radius a: Inner radius l: Length
Circular loop	$r\cdot \left(\ln {\frac {8r}{a}}-2+Y\right)$	r: Loop radius a: Wire radius
Rectangle	${\frac {1}{\pi }}\left(b\ln {\frac {2b}{a}}+d\ln {\frac {2d}{a}}-\left(b+d\right)\left(2-Y\right)+2{\sqrt {b^{2}+d^{2}}}-b\cdot \operatorname {arsinh} {\frac {b}{d}}-d\cdot \operatorname {arsinh} {\frac {d}{b}}\right)$	b, d: Border length d >> a, b >> a a: Wire radius
Pair of parallel wires	${\frac {l}{\pi }}\left(\ln {\frac {d}{a}}+Y\right)$	a: Wire radius d: Distance, d ≥ 2a l: Length of pair
Pair of parallel wires, high frequency	${\frac {l}{\pi }}\operatorname {arcosh} \left({\frac {d}{2a}}\right)={\frac {l}{\pi }}\ln \left({\frac {d}{2a}}+{\sqrt {{\frac {d^{2}}{4a^{2}}}-1}}\right)$	a: Wire radius d: Distance, d ≥ 2a l: Length of pair
Wire parallel to perfectly conducting wall	${\frac {l}{2\pi }}\left(\ln {\frac {2d}{a}}+Y\right)$	a: Wire radius d: Distance, d ≥ a l: Length
Wire parallel to conducting wall, high frequency	${\frac {l}{2\pi }}\operatorname {arcosh} \left({\frac {d}{a}}\right)={\frac {l}{2\pi }}\ln \left({\frac {d}{a}}+{\sqrt {{\frac {d^{2}}{a^{2}}}-1}}\right)$	a: Wire radius d: Distance, d ≥ a l: Length

The symbol μ₀ denotes the magnetic constant (4π×10⁻⁷ H/m). For high frequencies the electric current flows in the conductor surface (skin effect), and depending on the geometry it sometimes is necessary to distinguish low and high frequency inductances. This is the purpose of the constant Y: Y = 0 when the current is uniformly distributed over the surface of the wire (skin effect), Y = 1/4 when the current is uniformly distributed over the cross section of the wire. In the high frequency case, if conductors approach each other, an additional screening current flows in their surface, and expressions containing Y become invalid. Details for some circuit types are available on another page.

 المقاومة وتحليل دارة فاسور

$Z_{L}=V/I=jL\omega \,$

حيث

j is the imaginary unit,

L is the inductance,

ω = 2πf is the angular frequency,

f is the frequency and

Lω = X_L is the inductive reactance.

 تطبيقات التحريض الكهرمغنطيسي

لظاهرة التحريض الكهرمغنطيسي عددٌ من التطبيقات فيما يلي بعضها:

1 ـ المولدات التحريضية: وهي تعطي قوة محركة كهربائية إما متناوبة كما في المنوبات، أو متصلة كما في الدينامو. ويعتمد مبدأ تشغيلها على تغير التدفق في وشيعة تدور في مجال يوجد فيه حقل مغنطيسي ثابت.

2 ـ محولات التيار المتناوب: تتألف المحولة من دارة أولية مقترنة مغنطيسياً مع دارة ثانوية. إذا مر تيار متناوب في الأولية تحرض تيار متناوب في الثانوية بسبب التدفق الذي يجتازها لأنه ينتج عن حقل مغنطيسي متغير يولده تيار الأولية المتناوب.

3 ـ المحركات الكهربائية: يعتمد مبدأ تشغيل المحرك على مرور تيار كهربائي في وشيعة موضوعة في حقل مغنطيسي، فتؤثر فيها قوى مغنطيسية لها عزم يؤدي إلى دورانها.

4 ـ تسريع الإلكترونات في المسرِّعات: يستخدم الحقل الكهربائي المتحرض الناتج عن تغير التدفق لتوليد (ق.م.ك) تعمل على تسريع الإلكترونات في البيتاترون. [الذي يُعدّ مثالاً حياً لواقعية الحقول الكهربائية المتحرضة].

5 ـ هناك كثرة من التطبيقات تعتمد على تيارات فوكو كالتسخين في أفران التحريض وكالتخميد أو الكبح المغنطيسي في الأجهزة التي تعمل على التحريض.

 انظر أيضا

• تيار متردد
• حث مغناطيسي
• Dot convention
• Eddy current
• Electromagnetic induction
• كهربية
• Faraday's law of induction
• Gyrator
• Hydraulic analogy
• Inductor
• Leakage inductance
• LC circuit
• Magnetomotive force (MMF)
• RLC circuit
• RL circuit
• SI electromagnetism units
• Solenoid
• ناقل
• Kinetic inductance

 مراجع عامة

• Frederick W. Grover (1952). Inductance Calculations. Dover Publications, New York.
• Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
• Wangsness, Roald K. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 0-471-81186-6.
• Hughes, Edward. (2002). Electrical & Electronic Technology (8th ed.). Prentice Hall. ISBN 0-582-40519-X.
• Küpfmüller K., Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959.
• Heaviside O., Electrical Papers. Vol.1. – L.; N.Y.: Macmillan, 1892, p. 429-560.
• F. Langford-Smith, editor, 1953, Radiotron Designer's Handbook, 4th Edition, Wireless Press for Amalgamated Wireless Valve Company PTY, LTD, Sydney, Australia together with Eectron Tube Division of the Radio Corporation of America [RCA], Harrison, N. J. No Library of Congress Card Catalog Number or ISBN. Chapter 10 pp. 429-448 Calculation of Inductance includes a wealth of approximate formulas and nomographs for single-layer solenoids of various coil diameters and pitch of windings and lengths, the effects of screens, formulas and nomographs for multilayer coils (long and short), for toroidal coils, for flat spirals, and a nomograph for the mutual inductance between coaxial solenoids. With 56 references.

 وصلات خارجية

• Clemson Vehicular Electronics Laboratory: Inductance Calculator