عشاري
| Regular decagon | |
|---|---|
 A regular decagon | |
| النوع | مضلع منتظم |
| الأضلاع والرؤوس | {{{p10 جانب}}} |
| رمز شلفلي | {{{p10-شلفلي}}} |
| مخططات كوكستر-دنكن | |
| مجموعة التماثل | Dihedral (D10), order 2×10 |
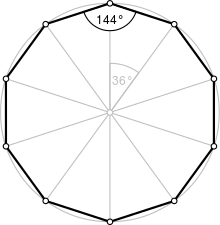
| الزاوية الداخلية (الدرجات) | 144° |
| الخصائص | Convex, cyclic, equilateral, isogonal, isotoxal |
في الهندسة الرياضية، العشاري decagon هو أي مضلع له عشرة أضلاع.[1]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
العشاري المنتظم
العشاري المنتظم بحيث تكون أطوال جميع أضلاعه متساوية وجميع زواياه متطابقة بزاوية 144°،[1] Its Schläfli symbol is {10} [2] ويمكن إنشاؤه كمضلع truncated، t{5}، عشاري شبه منتظم يتبادل فيه نوعان من الأضلاع.
المساحة
تعطى مساحة العشاري المنتظم ذو طول الضلع a بالعلاقة[3]:
In terms of the apothem r (see also inscribed figure), the area is:
In terms of the circumradius R, the area is:
An alternative formula is where d is the distance between parallel sides, or the height when the decagon stands on one side as base, or the diameter of the decagon's inscribed circle. By simple trigonometry,
and it can be written algebraically as
الأضلع
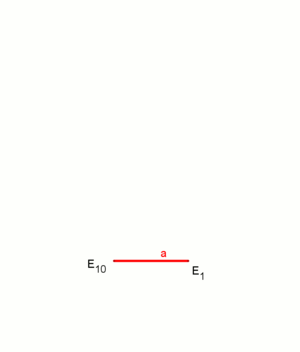
طول ضلع العشاري المنتظم المرسوم داخل دائرة الوحدة هو ، حيث ϕ هي النسبة الذهبية، .[4]
الإنشاء
As 10 = 2 × 5, a power of two times a Fermat prime, it follows that a regular decagon is constructible using compass and straightedge, or by an edge-bisection of a regular pentagon.[4]
An alternative (but similar) method is as follows:
- Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
- Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon.
- The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.
العشاري المنتظم غير المحدب

The length ratio of two inequal edges of a golden triangle is the golden ratio, denoted or its multiplicative inverse:
So we can get the properties of a regular decagonal star, through a tiling by golden triangles that fills this star polygon.
النسبة الذهبية في العشاري
Both in the construction with given circumcircle[5] as well as with given side length is the golden ratio dividing a line segment by exterior division the determining construction element.
- In the construction with given circumcircle the circular arc around G with radius GE3 produces the segment AH, whose division corresponds to the golden ratio.
- In the construction with given side length[6] the circular arc around D with radius DA produces the segment E10F, whose division corresponds to the golden ratio.
التناظر
The regular decagon has Dih10 symmetry, order 20. There are 3 subgroup dihedral symmetries: Dih5, Dih2, and Dih1, and 4 cyclic group symmetries: Z10, Z5, Z2, and Z1.
التقطيع
| 10-cube projection | 40 rhomb dissection | |||
|---|---|---|---|---|
|

|

|
|
|

|
|
|

|

|
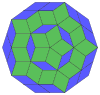
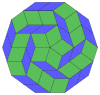
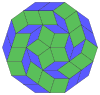
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.[7] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular decagon, m=5, and it can be divided into 10 rhombs, with examples shown below. This decomposition can be seen as 10 of 80 faces in a Petrie polygon projection plane of the 5-cube. A dissection is based on 10 of 30 faces of the rhombic triacontahedron. The list OEIS: A006245 defines the number of solutions as 62, with 2 orientations for the first symmetric form, and 10 orientations for the other 6.
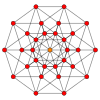 5-cube |
|
|
|

|

|

|
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
العشاري المنحرف
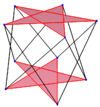
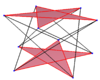
| {5}#{ } | {5/2}#{ } | {5/3}#{ } |
|---|---|---|

|
|
|
| A regular skew decagon is seen as zig-zagging edges of a pentagonal antiprism, a pentagrammic antiprism, and a pentagrammic crossed-antiprism. | ||
A skew decagon is a skew polygon with 10 vertices and edges but not existing on the same plane. The interior of such an decagon is not generally defined. A skew zig-zag decagon has vertices alternating between two parallel planes.
A regular skew decagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew decagon and can be seen in the vertices and side edges of a pentagonal antiprism, pentagrammic antiprism, and pentagrammic crossed-antiprism with the same D5d, [2+,10] symmetry, order 20.
These can also be seen in these 4 convex polyhedra with icosahedral symmetry. The polygons on the perimeter of these projections are regular skew decagons.
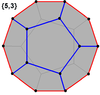 Dodecahedron |
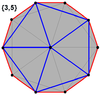 Icosahedron |
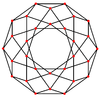 Icosidodecahedron |
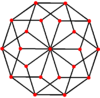 Rhombic triacontahedron |
مضلعات پتري
The regular skew decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these orthogonal projections in various Coxeter planes:[8] The number of sides in the Petrie polygon is equal to the Coxeter number, h, for each symmetry family.
| A9 | D6 | B5 | ||
|---|---|---|---|---|
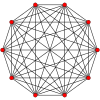 9-simplex |
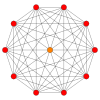 411 |
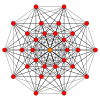 131 |
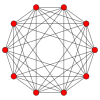 5-orthoplex |
 5-cube |
انظر أيضاً
- Decagonal number and centered decagonal number, figurate numbers modeled on the decagon
- Decagram, a star polygon with the same vertex positions as the regular decagon
المراجع
- ^ أ ب Sidebotham, Thomas H. (2003), The A to Z of Mathematics: A Basic Guide, John Wiley & Sons, p. 146, ISBN 9780471461630, https://books.google.com/books?id=VsAZa5PWLz8C&pg=PA146.
- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595, https://books.google.com/books?id=N8lX2T-4njIC&pg=PA9.
- ^ The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59, https://books.google.com/books?id=AW7qzTr_f1sC&pg=PA59. Note that this source uses a as the edge length and gives the argument of the cotangent as an angle in degrees rather than in radians.
- ^ أ ب Ludlow, Henry H. (1904), Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle, The Open Court Publishing Co., https://books.google.com/books?id=vLMlw7uL8kgC.
- ^ أ ب Green, Henry (1861), Euclid's Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II, London: Simpkin, Marshall,& CO., p. 116, https://books.google.de/books?id=DjQDAAAAQAAJ&pg=PA116&dq=II.+Practically+decagon+Euklid+p.+116&hl=de&sa=X&ved=0ahUKEwj0oJXvr-7KAhVEYpoKHQ2OCW0Q6AEIHTAA#v=onepage&q=II.%20Practically%20decagon%20Euklid%20p.%20116&f=false. Retrieved 10 February 2016.
- ^ أ ب Köller, Jürgen (2005) (in de), Regelmäßiges Zehneck, → 3. Section "Formeln, Ist die Seite a gegeben ...", http://www.mathematische-basteleien.de/zehneck.htm. Retrieved 10 February 2016.
- ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ^ Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.
وصلات خارجية
- Eric W. Weisstein, Decagon at MathWorld.
- Definition and properties of a decagon With interactive animation