عشروني الأوجه

عشروني الأوجه منتظم محدب

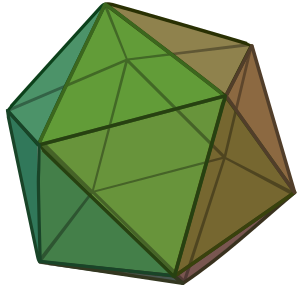
في الهندسة، عشروني الأوجه (icosahedron ؛ /ˌaɪkɒsəˈhiːdrən,_ʔkəʔ,_ʔkoʊʔ/ أو /aɪˌkɒsəˈhiːdrən/) هو متعدد الأسطح بعشرين وجه. الاسم اللاتيني يأتي من من يونانية قديمة εἴκοσι (إيْكوسي)، وتعني "عشرون", و ἕδρα (هيدرا)، وتعني "مقعد". صيغة الجمع تكون إما "icosahedra" ( /ʔdrə/) أو "icosahedrons".

There are many kinds of icosahedra, with some being more symmetrical than others. The best known is the Platonic, convex regular icosahedron.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 عشرونيات الأوجه المنتظمة

نوعان من عشرونيات الأوجه المنتظمة

عشروني الأوجه منتظم محدب

عشروني الأوجه الكبير

There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a great icosahedron.

 عشروني الأوجه منتظم محدب

المقالة الرئيسية: عشروني الأوجه منتظم

The convex regular icosahedron is usually referred to simply as the regular icosahedron, one of the five regular Platonic solids, and is represented by its Schläfli symbol {3, 5}, containing 20 triangular faces, with 5 faces meeting around each vertex.

Its dual polyhedron is the regular dodecahedron {5, 3} having three regular pentagonal faces around each vertex.

 عشروني الأوجه الكبير

المقالة الرئيسية: عشروني الأوجه الكبير

The great icosahedron is one of the four regular star Kepler-Poinsot polyhedra. Its Schläfli symbol is {3, 5/2}. Like the convex form, it also has 20 equilateral triangle faces, but its vertex figure is a pentagram rather than a pentagon, leading to geometrically intersecting faces. The intersections of the triangles do not represent new edges.

Its dual polyhedron is the great stellated dodecahedron {5/2, 3}, having three regular star pentagonal faces around each vertex.

 عشرونيات الأوجه النجمية

Stellation is the process of extending the faces or edges of a polyhedron until they meet to form a new polyhedron. It is done symmetrically so that the resulting figure retains the overall symmetry of the parent figure.

In their book The Fifty-Nine Icosahedra, Coxeter et al. enumerated 58 such stellations of the regular icosahedron.

Of these, many have a single face in each of the 20 face planes and so are also icosahedra. The great icosahedron is among them.

Other stellations have more than one face in each plane or form compounds of simpler polyhedra. These are not strictly icosahedra, although they are often referred to as such.

Notable stellations of the icosahedron
Regular	Uniform duals			Regular compounds			Regular star	Others
(Convex) icosahedron	Small triambic icosahedron	Medial triambic icosahedron	Great triambic icosahedron	Compound of five octahedra	Compound of five tetrahedra	Compound of ten tetrahedra	Great icosahedron	Excavated dodecahedron	Final stellation
The stellation process on the icosahedron creates a number of related polyhedra and مركبات بتماثل عشريني الأوجه.

 Pyritohedral symmetry

Pyritohedral and tetrahedral symmetries
Coxeter diagrams	(pyritohedral) (tetrahedral)
Schläfli symbol	s{3,4} sr{3,3} or $s{\begin{Bmatrix}3\\3\end{Bmatrix}}$
Faces	20 triangles: 8 equilateral 12 isosceles
Edges	30 (6 short + 24 long)
Vertices	12
Symmetry group	Th, [4,3+], (3*2), order 24
Rotation group	Td, [3,3]+, (332), order 12
Dual polyhedron	Pyritohedron
Properties	convex
Net
A regular icosahedron is topologically identical to a cuboctahedron with its 6 square faces bisected on diagonals with pyritohedral symmetry.

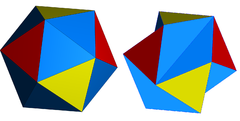
A regular icosahedron can be distorted or marked up as a lower pyritohedral symmetry, and is called a snub octahedron, snub tetratetrahedron, snub tetrahedron, and pseudo-icosahedron. This can be seen as an alternated truncated octahedron. If all the triangles are equilateral, the symmetry can also be distinguished by colouring the 8 and 12 triangle sets differently.

Pyritohedral symmetry has the symbol (3*2), [3⁺,4], with order 24. Tetrahedral symmetry has the symbol (332), [3,3]⁺, with order 12. These lower symmetries allow geometric distortions from 20 equilateral triangular faces, instead having 8 equilateral triangles and 12 congruent isosceles triangles.

These symmetries offer Coxeter diagrams: and respectively, each representing the lower symmetry to the regular icosahedron , (*532), [5,3] icosahedral symmetry of order 120.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الإحداثيات الكارتيزية

Construction from the vertices of a truncated octahedron, showing internal rectangles.

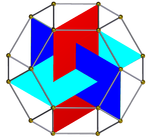
The coordinates of the 12 vertices can be defined by the vectors defined by all the possible cyclic permutations and sign-flips of coordinates of the form (2, 1, 0). These coordinates represent the truncated octahedron with alternated vertices deleted.

This construction is called a snub tetrahedron in its regular icosahedron form, generated by the same operations carried out starting with the vector (ϕ, 1, 0), where ϕ is the golden ratio.

 عشروني أوجه جسن

The regular icosahedron and Jessen's icosahedron.

المقالة الرئيسية: Jessen's icosahedron

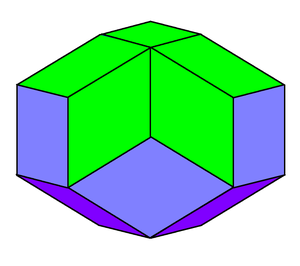
In Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, the 12 isosceles faces are arranged differently such that the figure is non-convex. It has right dihedral angles.

It is scissors congruent to a cube, meaning that it can be sliced into smaller polyhedral pieces that can be rearranged to form a solid cube.

 عشرونيات الأوجه الأخرى

Rhombic icosahedron

 عشروني الأوجه المعينة

المقالة الرئيسية: عشروني الأوجه المعينة

The rhombic icosahedron is a zonohedron made up of 20 congruent rhombs. It can be derived from the rhombic triacontahedron by removing 10 middle faces. Even though all the faces are congruent, the rhombic icosahedron is not face-transitive.

 تماثلات الهرم والمخروط

Common icosahedra with pyramid and prism symmetries include:

• 19-sided pyramid (plus 1 base = 20).
• 18-sided prism (plus 2 ends = 20).
• 9-sided antiprism (2 sets of 9 sides + 2 ends = 20).
• 10-sided bipyramid (2 sets of 10 sides = 20).
• 10-sided trapezohedron (2 sets of 10 sides = 20).

 جواسئ جونسون

Several Johnson solids are icosahedra:

J22	J35	J36	J59	J60	J92
Gyroelongated triangular cupola	Elongated triangular orthobicupola	Elongated triangular gyrobicupola	Parabiaugmented dodecahedron	Metabiaugmented dodecahedron	Triangular hebesphenorotunda
16 triangles 3 squares   1 hexagon	8 triangles 12 squares	8 triangles 12 squares	10 triangles   10 pentagons	10 triangles   10 pentagons	13 triangles 3 squares 3 pentagons 1 hexagon

 انظر أيضاً

• 600-cell

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .