إسقاط مجسم
 |
| جزء من سلسلة عن: |
| الإسقاط الهندسي |
|---|
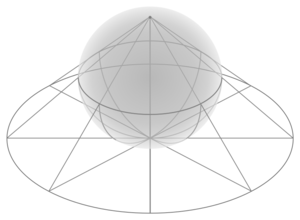
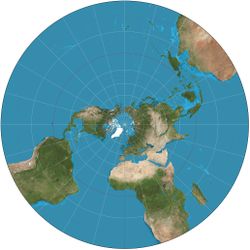
في الهندسة، الإسقاط المجسم stereographic projection، هو تخطيط دالة معينة تعكس كرة ما على مستوى. يُعين الإسقاط على الكرة بأكملها، عدا نقطة واحدة: نقطة الإسقاط. عند تعيينها، تكون الدالة ناعمة وتقابلية. يكون الإسقاط المجسم تشكيلياً، مما يعني أنه يحافظ على زوايا التقاء المنحيات. لا يكون الإسقاط المجسم تقايسياً] ولا محافظاً على المساحة: فهو لا يحافظ على المسافات ولا على مساحات الأشكال.
بديهياً، يعتبر الإسقاط المجسم طريقة لتصوير الكرة كمستوى، مع بعض المقاربات التي لا بد منها. لأن الكرة والمستوى يظهران في الكثير من مجالات الرياضيات وتطبيقاتها، لذلك، يستخدم الإسقاط المجسم في مختلف المجالات ومنها التحليل المركب، رسم الخرائط، الجيولوجيا، والتصوير الفوتوغرافي. عملياً، يتم تنفيذ الإسقاط عن طريق الحاسوب أو يدوياً باستخدام نوع معين من ورق الرسم البياني يسمى شبكة التجسيم أو شبكة وولف.
التاريخ

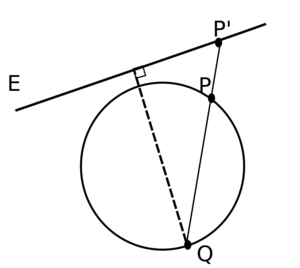
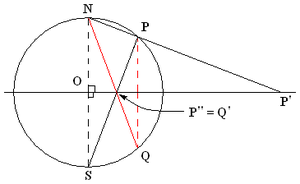
التعريف
الصيغة الأولى

تعريفات أخرى
تعميات
الخصائص
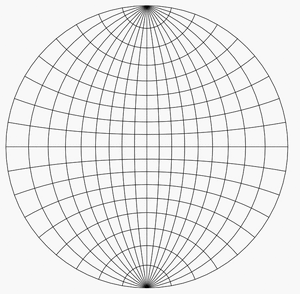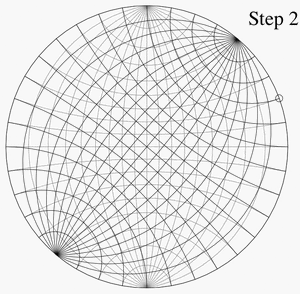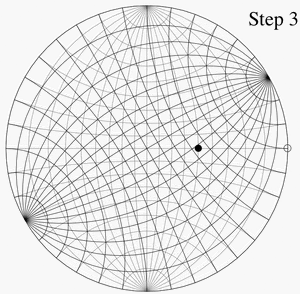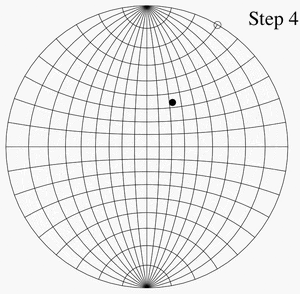
شبكة وولف
تطبيقات في الرياضيات
التحليل المركب
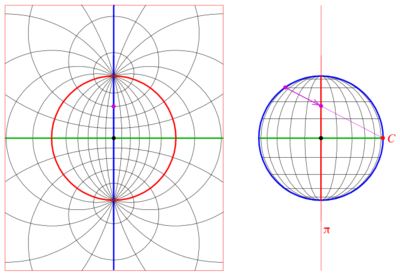
تصور الخطوط والكرات

تصوير آخر
الهندسة الحسابية

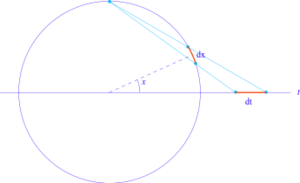
استبدال نصف زاوية المماس
تطبيقات في مجالات أخرى
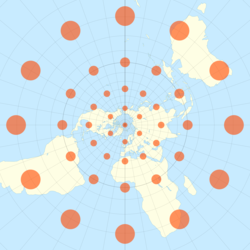
رسم الخرائط
The stereographic projection with Tissot's indicatrix of deformation.
علوم الكواكب

علم البلورات
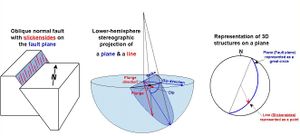
الجيولوجيا
التصوير الفوتوغرافي
انظر أيضاً
المصادر
المراجع
- Apostol, Tom (1974). Mathematical Analysis (2 ed.). Addison-Wesley. ISBN 0-201-00288-4.
- Brown, James; Churchill, Ruel (1989). Complex variables and applications. New York: McGraw-Hill. ISBN 0-07-010905-2.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - Casselman, Bill (2014), Feature column February 2014:Stereographic Projection, AMS, http://www.ams.org/samplings/feature-column/fc-2014-02, retrieved on 2014-12-12
- German, Daniel (June 2007). "Flattening the Viewable Sphere". "Proceedings of Computational Aesthetics 2007": 23–28, Banff: Eurographics.
- Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation and Lorentz Groups and their Applications, New York: Pergamon Press
- Do Carmo; Manfredo P. (1976). Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-212589-7.
- Elkins, James (1988). "Did Leonardo Develop a Theory of Curvilinear Perspective?: Together with Some Remarks on the 'Angle' and 'Distance' Axioms". Journal of the Warburg and Courtauld Institutes. The Warburg Institute. 51: 190–196. doi:10.2307/751275. JSTOR 751275.
- Oprea, John (2003). Differential geometry and applications. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-065246-6.
- Pedoe, Dan (1988). Geometry. Dover. ISBN 0-486-65812-0.
- Shafarevich, Igor (1995). Basic Algebraic Geometry I. Springer. ISBN 0-387-54812-2.
- Snyder, John P. (1987). Map Projections − A Working Manual, Professional Paper 1395. US Geological Survey.
- Snyder, John P. (1989). An Album of Map Projections, Professional Paper 1453. US Geological Survey.
- Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
- Spivak, Michael (1999). A comprehensive introduction to differential geometry, Volume IV. Houston, Texas: Publish or Perish. ISBN 0-914098-73-X.
وصلات خارجية
- Eric W. Weisstein, Stereographic projection at MathWorld.
- Stereographic Projection on PlanetMath
- Stereographic Projection and Inversion from Cut-the-Knot
- DoITPoMS Teaching and Learning Package - "The Stereographic Projection"
مرئيات
- Proof about Stereographic Projection taking circles in the sphere to circles in the plane
- Time Lapse Stereographic Projection on Vimeo
برمجيات
- Free and open source python program for stereographic projection - PTCLab
- Sphaerica software is capable of displaying spherical constructions in stereographic projection
- Three dimensional Java Applet