إسقاط دوراني

لمعلومات عن الإسقاط الدوراني في ألعاب الڤيديو وفن الپكسل، انظر الرسومات متساوية القياس في ألعاب الڤيديو وفن الپكسل.

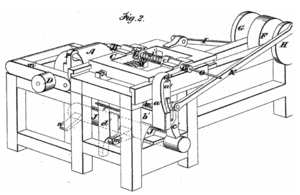
الإسقاط الدوراني Axonometric projection، هو أحد أنواع الإسقاطات العمودية يستخدم لإنشاء رسم مصور لجسم، حيث تكون خطوط الإبصار متعامدة مع مستوى الإسقاط، ويدور الجسم حول واحد أو أكثر من محاوره لكشف جوانب متعددة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 نظرة عامة

كلمة "دوراني" تعني "قابل للقياس على طول المحاور". يظهر الإسقاط الدوراني صورة الجسم كما تظهر من اتجاه منحرف من أجل الكشف عن أكثر من جانب للجسم في نفس الصورة. بينما تتضمن الإسقاطات متعددة المشاهد صور للأجسام من المشاهد الرئيسية الستة (أي، من الأمام، اليمين، اليسار، الأعلى، الأسفل، أو الخلف) حيث تكون محاور أو مستويات الجسم متوازية مع مستوى الإسقاط (ومن ثم لا تظهر إلا جانباً واحداً للجسم في كل مرة)، ففي الإسقاط الدوراي دائماً ما تُرسم المستويات أو المحاور الرئيسية للجسم غير موازية لمستوى المنظور.

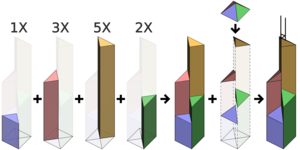
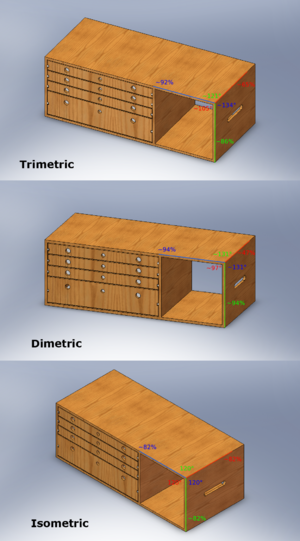
 الأنواع الثلاثة

مقارنة بين الأنواع المختلفة للإسقاط هندسي.

إسقاطات مختلفة وكيفية الحصول عليها.

المشاهد الدورانية الثلاثة. توضح النسبة المئوية نسبة القصور.

الأنواع الثلاثة للإسقاط الدوراني هي:

• الإسقاط مساو القياس: أكثر أشكال الإسقاط الدوراني شيوعاً في الرسم الهندسي،
• الإسقاط المتري الثنائي
• الإسقاط المتري الثلاثي

ويعتمد كل نوع منها على الزاوية الدقيقة التي ينحرف فيها المنظر عن العمود.

 التاريخ

• 

  Optical-grinding engine model (1822), drawn in 30° isometric perspective

• 

  Example of a dimetric perspective drawing from a US Patent (1874)

• 

  Example of a trimetric projection showing the shape of the Bank of China Tower in Hong Kong.

• 

  Example of isometric projection in Chinese art in an illustrated edition of the Romance of the Three Kingdoms, China, c. 15th century CE.

• 

  Detail of the original version of Along the River During the Qingming Festival attributed to Zhang Zeduan (1085–1145). Note that the picture switches back and forth between axonometric and perspective projection in different parts of the image.

 القيود

انظر أيضاً: جسم مستحيل

In this drawing, the blue sphere is two units higher than the red one. However, this difference in elevation is not apparent if one covers the right half of the picture.

The Penrose stairs depicts a staircase which seems to ascend (anticlockwise) or descend (clockwise) yet forms a continuous loop.

 قراءات إضافية

• Yve-Alain Bois, "Metamorphosis of Axonometry," Daidalos, no. 1 (1981), pp. 41–58