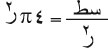هندسة المجسمات

هندسة المجسمات solid geometry هو فرع من الرياضيات يبحث في خواص الأشكال الهندسية في فضاء ثلاثي الأبعاد. ففي هذا الفضاء يمكن تعيين عدد غير منتهٍ من المستويات بحيث يمر مستوٍ واحد فقط من أي ثلاث نقط غير واقعة على استقامة واحدة. ويعد المستوي ممتداً إلى ما لانهاية في جميع الاتجاهات الواقعة عليه. فالمستوي يفصل الفضاء إلى منطقتين بحيث لا يمكن لأي مستقيم يصل بين نقطة من الأولى إلى نقطة من الثانية إلا ويكون قاطعاً للمستوي في نقطة واحدة ولا يمكن أن يقطعه في نقطتين، وإلا انطبق على المستوي نفسه.
والهندسة الفراغية أو الهندسة الصلبة هي الهندسة الإقليدية مطبقة في فضاء إقليدي ثلاثي الأبعاد مشابه للفضاء الذي نعيش فيه . تهتم الهندسة الفراغية بدراسة الأشكال الهندسية الثلاثية الأبعاد مثل المكعب ، الموشور ، المخروط
السطح المنشوري (الموشوري)
هو السطح المتولد من حركة مستقيم موازٍ لنفسه ويستند إلى مضلع غير واقع في مستويه.
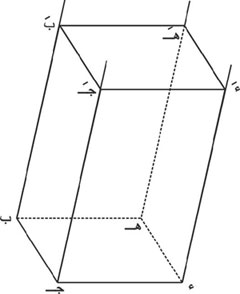
بفرض ب جـ د هـ مضلعاً والمستقيم ب بَ غير واقع في مستويه، إذا تحرك هذا المستقيم مع بقائه موازياً لنفسه وظل مستنداً إلى المضلع، فإنه يولد سطحاً منشورياً. (يسمى ب بَ مولد السطح، ويسمى المضلع ب جـ د هـ دليل السطح.)
ـ المجسمات: لنبدأ من أحد المجسمات البسيطة وهو المنشور (الموشور): نحصل على منشور بقطع السطح المنشوري بمستويين متوازيين، والاقتصار على الحيز الذي يحده السطح المنشوري والمستويان المتوازيان اللذان قطعاه. فهذا المجسم مكون من قاعدتين متوازيتين عليا وسفلى هما مضلعان طبوقان، وأوجهه الجانبية هي متوازيات أضلاع. وأبسط شكل للمنشور هو المكعب، قاعدتاه مربعان وأوجهه الجانبية هي أيضاً مربعات، وكلها طبوقة، فإذا كان ل هو طول ضلع كل من هذه المربعات تكون مساحة سطحه الخارجي كله 6ل2، أما حجمه فيساوي ل3.
ويلي المكعب متوازي المستطيلات، وهو منشور قاعدته مستطيل ومولده عمودي على القاعدة، وحجمه يساوي جداء طوله في عرضه في ارتفاعه.
وبوجه عام: حجم أي منشور يساوي جداء مساحة القاعدة في الارتفاع، (حيث الارتفاع هو طول العمود المشترك بين القاعدتين). أما السطح الخارجي فيحسب بجمع مساحات أوجهه كلها.
التاريخ
The Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonists. Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its radius.[1]
المواضيع
Basic topics in solid geometry and stereometry include
- incidence of planes and lines
- dihedral angle و زاوية مجسمة
- the cube, cuboid, parallelepiped
- the tetrahedron and other pyramids
- prisms
- octahedron, dodecahedron, icosahedron
- cones and cylinders
- the sphere
- other quadrics: spheroid, ellipsoid, paraboloid and hyperboloids.
Advanced topics include
- projective geometry of three dimensions (leading to a proof of Desargues' theorem by using an extra dimension)
- further polyhedra
- descriptive geometry.
أشكال مجسمة
Whereas a sphere is the surface of a ball, it is sometimes ambiguous whether the term refers to the surface of the figure or the volume enclosed therein, notably for a cylinder. The following table includes major types of shapes that either constitute or define a volume.
| Figure | Definitions | Images | |
|---|---|---|---|
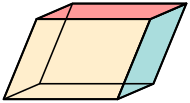
| Parallelepiped |
|
| |
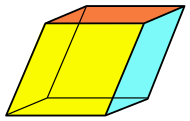
| Rhombohedron |
|
| |
| Cuboid |
|

| |
| Polyhedron | Flat polygonal faces, straight edges and sharp corners or vertices. | ||
| Uniform polyhedron | Regular polygons as faces and is vertex-transitive (i.e., there is an isometry mapping any vertex onto any other). |
| |
| Prism | A polyhedron comprising an n-sided polygonal base, a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. | 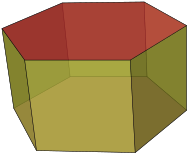
| |
| Cone | Tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. | ||
| Cylinder | Straight parallel sides and a circular or oval cross section. | ||
| Ellipsoid | A surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. | ||
| Lemon | A lens (or less than half of a circular arc) rotated about an axis passing through the endpoints of the lens (or arc).[4] | 
| |
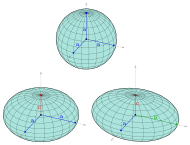
| Hyperboloid | A surface that generated by rotating a hyperbola around one of its principal axes. | 
|
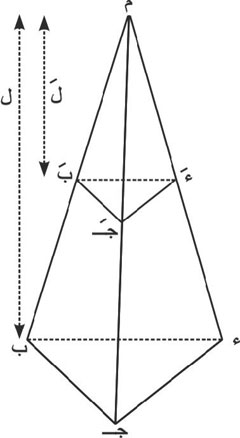
الهرم
يتكون من قاعدة مضلعة الشكل. وأوجهه الجانبية مثلثات لها رأس مشترك هو رأس الهرم.
الهرم الثلاثي
هو أبسط الأهرامات، وقاعدته مثلث.
حجم الهرم الثلاثي يساوي ثلث مساحة القاعدة في الارتفاع. لأن كل منشور ثلاثي يمكن تقسيمه إلى ثلاثة أهرامات ثلاثية متكافئة.
ولما كان بالإمكان تجزئة أي هرم إلى أهرام ثلاثية، كان حجم أي هرم يساوي أيضاً ثلث مساحة القاعدة في الارتفاع.
السطح الأسطواني
هو كالسطح المنشوري إلا أن دليله ل منحنٍ بدلاً من المضلع.
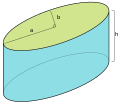
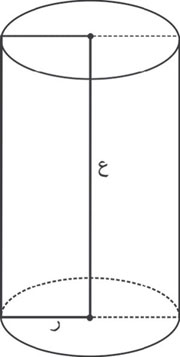
الأسطوانة
هي في الحقيقة منشور تحولت قاعدته المضلعة إلى منحنٍ مغلق. فحجم الأسطوانة يساوي جداء مساحة القاعدة في الارتفاع.
تكون الأسطوانة دورانية إذا كانت قاعدتها دائرة ومولداتها عمودية على مستوي هذه الدائرة. وتتولد الأسطوانة الدورانية من دوران مستطيل حول أحد أضلاعه. وإذا قص سطح هذه الأسطوانة وفرد يصبح مستطيلاً طوله هو محيط دائرة القاعدة وارتفاعه هو مولد السطح الأسطواني، فالسطح الجانبي لأسطوانة دورانية يساوي محيط القاعدة في المولد.
السطح المخروطي
هو السطح المتولد من حركة مستقيم يمر من نقطة ثابتة ويستند إلى منحنٍ. تسمى م رأس السطح، والمستقيم ب بَ مولده.
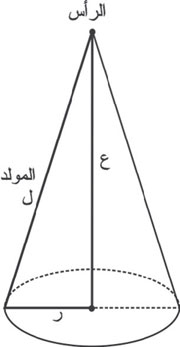
المخروط
هو هرم تحولت قاعدته إلى منحنٍ مغلق، فحجم المخروط يساوي ثلث مساحة القاعدة في الارتفاع.
دوران مثلث قائم حول إحدى ضلعيه القائمتين، فيتولد سطحه من دوران الوتر.
مساحة السطح الجانبي للمخروط الدوراني تساوي نصف محيط القاعدة في طول المولد.
الكرة
على فرض أن هناك نقطة م وعدداً ر. إن مجموعة نقط الفضاء التي تبعد عن م مسافة ر تشكل سطح كرة مركزها م ونصف قطرها ر.
بفرض ب نقطة في الفضاء تبعد عن مركز الكرة م مسافة ل.
فحين تكون ل = ر تكون النقطة ب على سطح الكرة. وحين تكون ل < ر تكون ب خارج الكرة. وحين تكون ل > ر تكون ب داخل الكرة. فالكرة سطح مغلق.
بفرض س مستقيماً يبعد عن مركز الكرة مسافة ج
حين تكون ج < ر، تكون جميع نقط هذا المستقيم خارج الكرة. وحين تكون ج = ر يكون المستقيم مماساً للكرة.
أما حين تكون ج > ر فيكون المستقيم قاطعاً للكرة في نقطتين. فيتعين عليه وتر
فإذا كان طرفا قطعة مستقيمة مثل ب جـ واقعين داخل الكرة، تكون القطعة بتمامها داخل الكرة. فالكرة سطح مغلق محدب.
إن وضع مستوي بالنسبة لكرة يتوقف أيضاً على بعد هذا المستوي عن مركز الكرة. فإذا كان هذا البعد أكبر من ر يكون المستوي خارج الكرة، وإذا كان هذا البعد يساوي ر يكون المستوي مماساً للكرة.
أما إذا كان هذا البعد أصغر من ر فيكون المستوي قاطعاً للكرة وفق دائرة مركزها هو مسقط مركز الكرة على المستوي .
وحين يكون المستوي ماراً من مركز الكرة فإنه يقطعها وفق دائرة قطرها هو قطر الكرة، وتوصف بأنها دائرة عظمى، لأنه لا يمكن أن توجد على سطح الكرة دائرة أكبر من ذلك.
مساحة سطح الكرة: لما كانت جميع الكرات متشابهة كانت مساحات سطوح الكرات متناسبة مع مربعات أنصاف أقطارها. أو بتعبير آخر إن النسبة بين مساحة سطح أي كرة ومربع نصف قطرها هي نسبة ثابتة وقد وجد أنها تساوي 4 π، فإذا رمزنا لمساحة سطح الكرة بالرمز سط يكون لدينا
ومنه سط = 4 π ر2، وهكذا فإن مساحة سطح الكرة هي أربعة أمثال مساحة دائرة عظمى عليها.
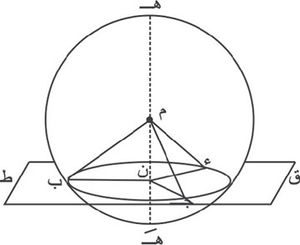
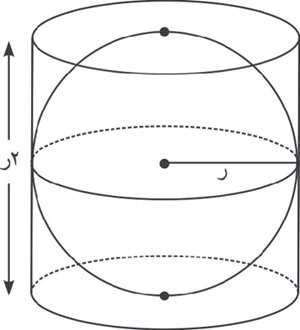
لتكن هناك أسطوانة دورانية (الشكل-9) مرسومة خارج الكرة بحيث يكون سطحها الجانبي ملامساً للكرة ومستوي كل من قاعدتيها مماس للكرة. إن مساحة السطح الجانبي لهذه الأسطوانة تساوي مساحة سطح الكرة؛ لأن كلاً منهما يساوي 4 π ر2.
المنطقة الكروية
هي منطقة من سطح الكرة محصورة بين مستويين متوازيين قاطعين للكرة .
إن مساحة هذه المنطقة تساوي مساحة المنطقة المقابلة لها من السطح الأسطواني التي ارتفاعها هو ارتفاع المنطقة الكروية أي ل إذاً مساحتها تساوي 2 π ر ل.
ملاحظة: يُستفاد من هذه العلاقة بين الكرة والأسطوانة في رسم خرائط مسطحة للكرة الأرضية.
القبة الكروية
هي منطقة كروية إحدى قاعدتيها هي مستوٍ مماس للكرة.
حجم الكرة
إذا جزئ سطح الكرة إلى أجزاء صغيرة يصبح انحناء الكرة في كل جزء منها ضعيفاً بحيث يمكن عد هذا الجزء مستوياً، ومن ثم يمكن عده قاعدة لمخروط رأسه في مركز الكرة. فحجم كل من هذه الأهرامات يساوي ثلث مساحة القاعدة في الارتفاع. والارتفاع كما يلاحظ هو- في كل الأهرامات - نصف قطر الكرة. فللحصول على حجم الكرة تجمع مساحات قواعد الأهرامات كلها فيحصل على سطح الكرة 4 π ر2 وثم يضرب بثلث نصف القطر (1/3)ل. فحجم الكرة يساوي (4/3) π ر3.
القطاع الكروي
هو جزء من الكرة قاعدته قبة كروية ورأسه مركز الكرة .
يُحسب حجم هذا القطاع بالطريقة نفسها التي اتبعت في حساب حجم الكرة أي بتجزئة القاعدة إلى أجزاء صغيرة يمكن عدها قواعد لمخاريط رأسها مشترك في مركز الكرة (فارتفاعها المشترك هو ر) ومجموعها هو مساحة سطح القبة، فحجم القطاع: (1/3) (2 π ر. ل. ر) = (2/3) π ر2 ل.
حجم القبة الكروية
لحساب حجم القبة الكروية ب جـ د لَ يجب أن يحسب أولاً حجم القطاع الكروي، ثم يطرح منه حجم المخروط الذي قاعدته هي قاعدة القبة وارتفاعه م هـ حيث هـ هي مركز قاعدة القبة وهي مسقط مركز الكرة م على القاعدة...[5]
التقنيات
Various techniques and tools are used in solid geometry. Among them, analytic geometry and vector techniques have a major impact by allowing the systematic use of linear equations and matrix algebra, which are important for higher dimensions.
التطبيقات
A major application of solid geometry and stereometry is in computer graphics.
انظر أيضاً
- Ball regions
- Euclidean geometry
- Dimension
- Point
- Planimetry
- Shape
- Lists of shapes
- Surface
- Surface area
- أرخميدس
المصادر
الهامش
- ^ ...paraphrased and taken in part from the 1911 Encyclopædia Britannica.
- ^ Robertson, Stewart Alexander (1984). Polytopes and Symmetry. Cambridge University Press. p. 75. ISBN 9780521277396.
- ^ Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Retrieved December 1, 2018.
- ^ Weisstein, Eric W. "Lemon". Wolfram MathWorld. Retrieved 2019-11-04.
- ^ الهندسة الفراغية, الموسوعة العربية
المراجع
- Kiselev, A. P. (2008). Geometry. Vol. Book II. Stereometry. Translated by Givental, Alexander. Sumizdat.
{{cite book}}: Invalid|ref=harv(help)
| مواضيع في الهندسة الرياضية | |
| هندسة إقليدية ثلاثية الأبعاد (هندسة فراغية) | |
| إسقاط ثلاثي الأبعاد 3D projection| رسومات حاسوبية ثلاثية الأبعاد> تقسيم فضاء ثنائي > إقتفاء شعاع> مسح جراهام| حلقات بوروميان| كريستال| قضبان Cuisenaire| نظرية دي سارغو| مخروط دائري صحيح| مجسم زائد| مجسم درجة ثانية| متعدد سطوح> ( عيب (هندسة)| موشور| بريسماتويد Prismatoid | قرص عسل| هرم| متوازي الأنابيب Parallelepiped )| رباعي سطوح > ( رباعي سطوح هيروني| صلب أفلاطوني Platonic solid | صلب أرخميدي Archimedean solid| صلب كبلر بوينسوت| صلب جونسن| شكل متعدد السطوح موحد| مركب متعدد الوجوه Polyhedral| مشكلة هلبرت الثالثة| دلتاهيدرون Deltahedron )| سطح نظامي Surface normal| مجال 3، جسم شبه كروي spheroid ، مجسم ناقص ellipsoid | مكبر صوت قطعي مكافىء Parabolic microphone | عاكس قطعي مكافىء Parabolic reflector| مقطع عرضي Cross section| سفيريكون Sphericon| إسقاط رسومي فراغي Stereographic| قياسات فراغية Stereometry |