معامل جيني
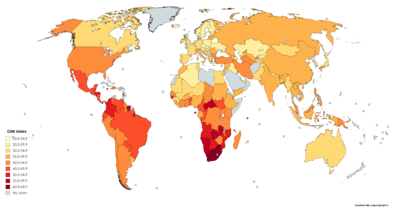
معامل جيني في علم الاقتصاد ، يُعد المعامل الجيني ، الذي يُطلق عليه أحيانًا مؤشر جيني أو نسبة جيني ، مقياسًا للتشتت الإحصائي الذي يهدف إلى تمثيل عدم المساواة في الدخل أو عدم المساواة في الثروة داخل دولة أو أي مجموعة أخرى من الناس. تم تطويره بواسطة الإحصائي وعالم الاجتماع الإيطالي كورادو جيني ونشر في مقالته التي صدرت عام 1912 بعنوان التباين والتغير (بالإيطالية: Variabilità e mutabilità)(إيطالية: Variabilità e mutabilità).[2][3]
يقيس معامل جيني عدم المساواة بين قيم متغيرة(على سبيل المثال ، مستويات الدخل). يعبر معامل جيني للصفر عن المساواة الكاملة ، حيث تكون جميع القيم متماثلة (على سبيل المثال ، حيث يحصل كل فرد على نفس الدخل). يعبر معامل جيني بواحد (أو 100٪) عن الحد الأقصى من عدم المساواة بين القيم (على سبيل المثال ، بالنسبة لعدد كبير من الأشخاص حيث يكون لدى شخص واحد فقط كل الدخل أو الاستهلاك بينما لا يملك الآخرون أي شيء ، فإن معامل جيني سيكون واحدًا تقريبًا).[4][5]
بالنسبة للمجموعات الأكبر ، القيم القريبة من واحد غير محتملة. بالنظر إلى تطبيع كل من السكان التراكميين والحصة التراكمية للدخل المستخدمة لحساب معامل جيني ، فإن المقياس لا يتأثر بشكل مفرط بخصائص توزيع الدخل ، بل فقط لكيفية اختلاف الدخل بالنسبة للأعضاء الآخرين من السكان . الاستثناء من ذلك هو إعادة توزيع الدخل مما يؤدي إلى الحد الأدنى من الدخل لجميع الناس. عندما يتم فرز السكان ، إذا كان توزيع الدخل يقارب دالة معروفة جيدًا ، فيمكن عندئذٍ حساب بعض القيم التمثيلية.
تم اقتراح معامل جيني من قبل جيني كمقياس لعدم المساواة في الدخل أو الثروة.[6] بالنسبة لبلدان منظمة التعاون الاقتصادي والتنمية ، في أواخر القرن العشرين ، بالنظر إلى تأثير الضرائب ومدفوعات التحويل ، تراوح معامل جيني للدخل بين 0.24 و 0.49 ، وكانت سلوفينيا هي الأدنى والمكسيك الأعلى.[7] [8][9] كان لدى البلدان الأفريقية أعلى معاملات جيني قبل الضرائب في 2008-2009 ، مع جنوب إفريقيا الأعلى في العالم ، ويقدر بشكل مختلف ما بين 0.63 إلى 0.7 ، على الرغم من انخفاض هذا الرقم إلى 0.52 بعد أخذ المساعدة الاجتماعية في الاعتبار ، وتنخفض مرة أخرى إلى 0.47 بعد الضرائب. [10] قدر معامل جيني للدخل العالمي في عام 2005 بما يتراوح بين 0.61 و 0.68 من خلال مصادر مختلفة.[11][12]
هناك بعض المشكلات في تفسير معامل جيني. قد تنتج نفس القيمة عن العديد من منحنيات التوزيع المختلفة. يجب أن يؤخذ الهيكل الديموغرافي في الاعتبار. تشهد البلدان التي بها شيخوخة سكانية ، أو التي تشهد طفرة في المواليد ، زيادة في معامل جيني قبل الضرائب حتى لو ظل توزيع الدخل الحقيقي للبالغين العاملين ثابتًا. ابتكر العلماء أكثر من عشرة أنواع مختلفة من معامل جيني.[13][14][15]
التاريخ
التعريف
طريقة الحساب
مثال: مستويان من الدخل
التعبيرات البديلة
توزيع احتمالي منفصل
التوزيع الاحتمالي المستمر
مناهج أخرى
مؤشرات عدم المساواة المعممة
من توزيعات الدخل
مؤشرات جيني للدخل الإقليمي
مؤشر جيني للدخل العالمي منذ القرن التاسع عشر
دول حسب مؤشر جيني
التنمية الاجتماعية
التعليم
الفرصة
تنقل الدخل
ميزات
القيود
بدائل
العلاقة بالمقاييس الإحصائية الأخرى
انظر ايضا
- Diversity index
- Economic inequality
- Great Gatsby curve
- Herfindahl index
- Hoover index (a.k.a. Robin Hood index)
- Human Poverty Index
- Income inequality metrics
- Kuznets curve
- List of countries by distribution of wealth
- List of countries by income equality
- List of countries by inequality-adjusted HDI
- List of U.S. states by Gini coefficient
- Matthew effect
- Pareto distribution
- ROC analysis
- Social welfare provision
- Suits index
- Utopia
- Welfare economics
المصادر
- ^ "GINI index (World Bank estimate) | Data". data.worldbank.org. Retrieved 2020-07-23.
- ^ Gini (1912).
- ^ Gini, C. (1909). "Concentration and dependency ratios" (in Italian). English translation in Rivista di Politica Economica, 87 (1997), 769–789.
- ^ "Current Population Survey (CPS) – Definitions and Explanations". US Census Bureau.
- ^ Note: Gini coefficient could be near one only in a large population where a few persons has all the income. In the special case of just two people, where one has no income and the other has all the income, the Gini coefficient is 0.5. For five people, where four have no income and the fifth has all the income, the Gini coefficient is 0.8. See: FAO, United Nations – Inequality Analysis, The Gini Index Module (PDF format), fao.org.
- ^ Gini, C. (1936). "On the Measure of Concentration with Special Reference to Income and Statistics", Colorado College Publication, General Series No. 208, 73–79.
- ^ "Income distribution – Inequality: Income distribution – Inequality – Country tables". OECD. 2012. Archived from the original on 9 November 2014.
- ^ "South Africa Snapshot, Q4 2013" (PDF). KPMG. 2013. Archived from the original (PDF) on 24 مايو 2014.
- ^ "Gini Coefficient". United Nations Development Program. 2012. Archived from the original on 12 يوليو 2014.
- ^ Schüssler, Mike (16 July 2014). "The Gini is still in the bottle". Money Web. Retrieved 24 November 2014.
- ^ Hillebrand, Evan (يونيو 2009). "Poverty, Growth, and Inequality over the Next 50 Years" (PDF). FAO, United Nations – Economic and Social Development Department. Archived from the original (PDF) on 20 أكتوبر 2017.
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةundp10 - ^ Yitzhaki, Shlomo (1998). "More than a Dozen Alternative Ways of Spelling Gini" (PDF). Economic Inequality. 8: 13–30.
- ^ Sung, Myung Jae (August 2010). "Population Aging, Mobility of Quarterly Incomes, and Annual Income Inequality: Theoretical Discussion and Empirical Findings". CiteSeerX 10.1.1.365.4156.
{{cite journal}}: Cite journal requires|journal=(help) - ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةblomq81
قراءات اضافية
- Amiel, Y.; Cowell, F. A. (1999). Thinking about Inequality. Cambridge. ISBN 978-0-521-46696-7.
- Anand, Sudhir (1983). Inequality and Poverty in Malaysia. New York: Oxford University Press. ISBN 978-0-19-520153-6.
- Brown, Malcolm (1994). "Using Gini-Style Indices to Evaluate the Spatial Patterns of Health Practitioners: Theoretical Considerations and an Application Based on Alberta Data". Social Science & Medicine. 38 (9): 1243–1256. doi:10.1016/0277-9536(94)90189-9. PMID 8016689.
- Chakravarty, S. R. (1990). Ethical Social Index Numbers. New York: Springer-Verlag. ISBN 978-0-387-52274-6.
- Deaton, Angus (1997). Analysis of Household Surveys. Baltimore MD: Johns Hopkins University Press. ISBN 978-0-585-23787-9.
- Dixon, Philip M.; Weiner, Jacob; Mitchell-Olds, Thomas; Woodley, Robert (1987). "Bootstrapping the Gini coefficient of inequality". Ecology. 68 (5): 1548–1551. doi:10.2307/1939238. JSTOR 1939238. S2CID 84940050.
- Dorfman, Robert (1979). "A Formula for the Gini Coefficient". The Review of Economics and Statistics. 61 (1): 146–149. doi:10.2307/1924845. JSTOR 1924845.
- Firebaugh, Glenn (2003). The New Geography of Global Income Inequality. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-01067-3.
- Gastwirth, Joseph L. (1972). "The Estimation of the Lorenz Curve and Gini Index". The Review of Economics and Statistics. 54 (3): 306–316. doi:10.2307/1937992. JSTOR 1937992.
- Giles, David (2004). "Calculating a Standard Error for the Gini Coefficient: Some Further Results" (PDF). Oxford Bulletin of Economics and Statistics. 66 (3): 425–433. CiteSeerX 10.1.1.202.6462. doi:10.1111/j.1468-0084.2004.00086.x. S2CID 16972099. Archived from the original (PDF) on 5 May 2004.
- Gini, Corrado (1912). Variabilità e mutabilità. Reprinted in Pizetti, E.; Salvemini, T., eds. (1955). Memorie di metodologica statistica. Rome: Libreria Eredi Virgilio Veschi.
- Gini, Corrado (1921). "Measurement of Inequality of Incomes". The Economic Journal. 31 (121): 124–126. doi:10.2307/2223319. JSTOR 2223319.
- Giorgi, Giovanni Maria (1990). "Bibliographic portrait of the Gini concentration ratio" (PDF). Metron. 48: 183–231. Archived from the original (PDF) on 4 August 2016.
- Karagiannis, E.; Kovacevic, M. (2000). "A Method to Calculate the Jackknife Variance Estimator for the Gini Coefficient". Oxford Bulletin of Economics and Statistics. 62: 119–122. doi:10.1111/1468-0084.00163.
- Mills, Jeffrey A.; Zandvakili, Sourushe (1997). "Statistical Inference via Bootstrapping for Measures of Inequality" (PDF). Journal of Applied Econometrics. 12 (2): 133–150. CiteSeerX 10.1.1.172.5003. doi:10.1002/(SICI)1099-1255(199703)12:2<133::AID-JAE433>3.0.CO;2-H. hdl:10419/186818. JSTOR 2284908.
- Modarres, Reza; Gastwirth, Joseph L. (2006). "A Cautionary Note on Estimating the Standard Error of the Gini Index of Inequality". Oxford Bulletin of Economics and Statistics. 68 (3): 385–390. doi:10.1111/j.1468-0084.2006.00167.x. S2CID 122716409.
- Morgan, James (1962). "The Anatomy of Income Distribution". The Review of Economics and Statistics. 44 (3): 270–283. doi:10.2307/1926398. JSTOR 1926398.
- Ogwang, Tomson (2000). "A Convenient Method of Computing the Gini Index and its Standard Error". Oxford Bulletin of Economics and Statistics. 62: 123–129. doi:10.1111/1468-0084.00164.
- Ogwang, Tomson (2004). "Calculating a Standard Error for the Gini Coefficient: Some Further Results: Reply". Oxford Bulletin of Economics and Statistics. 66 (3): 435–437. doi:10.1111/j.1468-0084.2004.00087.x. S2CID 122160535.
- Xu, Kuan (January 2004). "How Has the Literature on Gini's Index Evolved in the Past 80 Years?" (PDF). Department of Economics, Dalhousie University. Archived from the original (PDF) on 28 September 2006. Retrieved 1 June 2006.
{{cite journal}}: Cite journal requires|journal=(help) The Chinese version of this paper appears in Xu, Kuan (2003). "How Has the Literature on Gini's Index Evolved in the Past 80 Years?". China Economic Quarterly. 2: 757–778. - Yitzhaki, Shlomo (1991). "Calculating Jackknife Variance Estimators for Parameters of the Gini Method". Journal of Business and Economic Statistics. 9 (2): 235–239. doi:10.2307/1391792. JSTOR 1391792.
وصلات خارجية
- Deutsche Bundesbank: Do banks diversify loan portfolios?, 2005 (on using e.g. the Gini coefficient for risk evaluation of loan portfolios)
- Forbes Article, In praise of inequality
- Measuring Software Project Risk With The Gini Coefficient, an application of the Gini coefficient to software
- The World Bank: Measuring Inequality
- Travis Hale, University of Texas Inequality Project:The Theoretical Basics of Popular Inequality Measures, online computation of examples: 1A, 1B
- Article from The Guardian analysing inequality in the UK 1974–2006
- World Income Inequality Database
- Income Distribution and Poverty in OECD Countries
- U.S. Income Distribution: Just How Unequal?