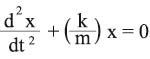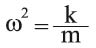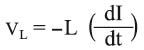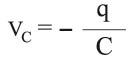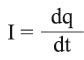هزاز توافقي
| ميكانيكا كلاسيكية | ||||||||
تاريخ...
| ||||||||
هزاز توافقي أو الحركة الاهتزازية oscillatory motion هي التكرار المستمر لحركة الأجسام حول موضع ثابت (موضع التوازن). وهي تصادف كثيراً في الطبيعة وفي الحياة اليومية مثل حركة نواس الساعة الجدارية، والمكبس داخل أسطوانة محرك، وحركة سطح ماء البحر، وكتلة معلقة بطرف نابض مرن مشدود، وحركة الذرات في الشبكة البلورية للجسم الصلب.
تعد الحركة الاهتزازية حالة خاصة من الحركة الدورية إذ إن الزمن اللازم لإتمام اهتزازة واحدة أي العودة إلى نقطة بدء الحركة متساو في كل الاهتزازات، و هو من أبرز صفات الحركة الاهتزازية، ويطلق عليه دور الحركة period، و يرمز له عادة بـ T.
تعرف الجملة التي يحصل فيها حركة اهتزازية بالجملة المهتزة oscillatory system. يمكن أن تكون قوى الإعادة إلى موضع التوازن في الجملة داخلية كقوة مرونة النابض، مما يولد حركات اهتزازية تسمى بالاهتزازات الحرة، أو قوى خارجية (خارج الجملة) كما هي الحال في اهتزاز غصن شجرة بتأثير قوة الرياح والتي تسمى بالاهتزازات القسرية forced oscillation.
تعد الكتلة المعلقة بطرف نابض أبسط الجمل الميكانيكية التي تمثل حركة اهتزازية ناجمة عن قوة داخلية متناسبة مع مقدار الإزاحة عن موضع التوازن ومعاكسة لها بالاتجاه بحسب العلاقة
- F = - kx،
حيث
- k ثابت مرونة النابض،
- x الإزاحة عن موضع التوازن (الشكل-1).
بتطبيق قانون نيوتن الثاني F = ma على حركة الكتلة والنابض في أثناء الاهتزاز، نجد أن معادلة حركة الكتلة المهتزة هي من الشكل:
هذه المعادلة حلها جيبي من الشكل:
- x = A cos (ωt + α)
حيث:
- A الازاحة العظمي (السعة) Amplitude،
- (ωt + α) طور الحركة،
- α الطور الابتدائي .
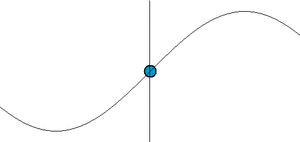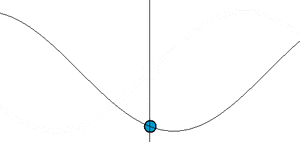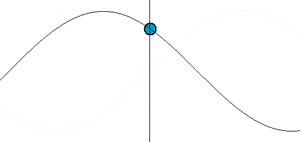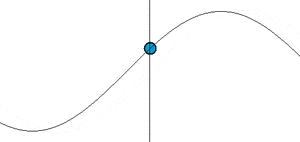
كل حركة اهتزازية يمكن وصفها بالمعادلة الجيبية السابقة تعرف أيضاً بالحركة التوافقية harmonic motion (الشكل-2).
وبالنظر إلى حركة الكتلة السابقة نجد أن سرعتها تمر بقيم عظمى وأخرى معدومة، مما يعني أن هناك تحول للطاقة الحركية إلى كامنة وبالعكس أيضاً بشكل مستمر، وهو ما يبرر استمرار عملية الاهتزاز.
الهزاز التوافقي البسيط
A simple harmonic oscillator is an oscillator that is neither driven nor damped. It consists of a mass m,which experiences a single force, F, which pulls the mass in the direction of the point x=0 and depends only on the mass's position x and a constant k. Newton's second law for the system is
Solving this differential equation, we find that the motion is described by the function
حيث
The motion is periodic— repeating itself in a sinusoidal fashion with constant amplitude, A. In addition to its amplitude, the motion of a simple harmonic oscillator is characterized by its period T, the time for a single oscillation or its frequency f = 1⁄T, the number of cycles per unit time. The position at a given time t also depends on the phase, φ, which determines the starting point on the sine wave. The period and frequency are determined by the size of the mass m and the force constant k, while the amplitude and phase are determined by the starting position and velocity.
The velocity and acceleration of a simple harmonic oscillator oscillate with the same frequency as the position but with shifted phases. The velocity is maximum for zero displacement, while the acceleration is in the opposite direction as the displacement.
The potential energy stored in a simple harmonic oscillator at position x is
الهزّاز التوافقي البسيط
 مقالة مفصلة: الهزّاز التوافقي البسيط
مقالة مفصلة: الهزّاز التوافقي البسيط
تخميد الهزاز التوافقي
 مقالة مفصلة: التثبيط
مقالة مفصلة: التثبيط
هزاز حدودي
 مقالة مفصلة: هزاز حدودي
مقالة مفصلة: هزاز حدودي
معادلة الهزاز العامة
نظم المعادلة
| Translational Mechanical | Torsional Mechanical | Series RLC Circuit | Parallel RLC Circuit |
|---|---|---|---|
| Position | Angle | Charge | Voltage |
| Velocity | Angular velocity | Current | |
| Mass | Moment of inertia | Inductance | Capacitance |
| Spring constant | Torsion constant | Elastance | Susceptance |
| Friction | Rotational friction | Resistance | Conductance |
| Drive force | Drive torque | ||
| Undamped resonant frequency : | |||
| Differential equation: | |||
Application to a conservative force
الهزازات التوافقية المشتقة
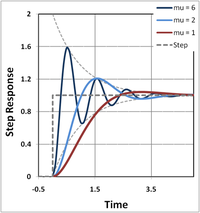
Step input
القوة الدافعة الجيبية
في حالة قوة دافعة جيبية:
where is the driving amplitude and is the driving frequency for a sinusoidal driving mechanism. This type of system appears in AC driven RLC circuits (resistor-inductor-capacitor) and driven spring systems having internal mechanical resistance or external air resistance.
الحل العام هو مجموع حل عابر يعتمد على الأحوال الابتدائية، وsteady state that is independent of initial conditions and depends only on the driving amplitude , driving frequency, , undamped angular frequency , and the damping ratio .
حل الحالة المنتظمة يتناسب مع القوة الدافعة بتغير في الطور المحثوث قدره :
حيث
is the absolute value of the impedance or linear response function and
is the phase of the oscillation relative to the driving force, if the arctan value is taken to be between -180 degrees and 0 (that is, it represents a phase lag, for both positive and negative values of the arctan's argument).
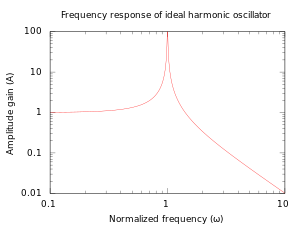
For a particular driving frequency called the resonance, or resonant frequency , the amplitude (for a given ) is maximum. This resonance effect only occurs when , i.e. for significantly underdamped systems. For strongly underdamped systems the value of the amplitude can become quite large near the resonance frequency.
The transient solutions are the same as the unforced () damped harmonic oscillator and represent the systems response to other events that occurred previously. The transient solutions typically die out rapidly enough that they can be ignored.
الذبذبات الكهربائية
 مقالة مفصلة: الذبذبات الكهربائية
مقالة مفصلة: الذبذبات الكهربائية
إن مفهوم الحركة الاهتزازية لا ينحصر فقط في الإزاحة الميكانيكية للجسم عن موضع التوازن، بل يحدث مثل ذلك أيضاً في الظواهر الكهربائية. كما أن القوانين التي تخضع لها الحركات الاهتزازية الكهربائية تشبه إلى حد كبير الاهتزازات الميكانيكية.
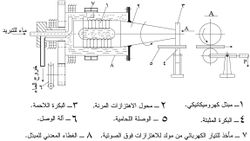
لتكن دارة كهربائية مؤلفة من مكثف كهربائي وتحريضية (وشيعة) وقاطعة، والتي يمكن أن نطلق عليها أيضاً الدارة المهتزة oscillatory circuit. عند إغلاق القاطعة يمر في الدارة تيار كهربائي تزداد شدته مع الزمن مما يؤدي إلى إفراغ المكثف وتغير في التدفق المغنطيسي من خلال التحريضية، الأمر الذي يسبب توليد قوة محركة كهربائية في التحريضية تعمل على توليد التيار الكهربائي في الدارة عند إفراغ المكثف يعمل على شحن المكثف من جديد، وهكذا على نحو متكرر. ويكون تغير التيار الكهربائي في أثناء هذه العملية دورياً (الشكل-3).
إن العمل الكهربائي الناجم عن انتقال شحنة كهربائية q في دارة مغلقة مساوٍ للصفر، إذن فإن: W = qvC + qvL = 0 حيث:vL التوتر بين طرفي التحريضية وهو يساوي إلى:
أما vC التوتر بين طرفي المكثفة والذي يساوي:
C سعة المكثفة، I شدة التيار، ومن كون:
نجد أن معادلة العمل السابقة تأخذ الشكل التالي:
والتي تمثل معادلة الاهتزازة الكهربائية. حلها أيضاً جيبي من الشكل: q = q0 cos ω t، يبين أنه يجري في الدارة تيار مهتز أو متناوب سعته (شدته) متغيرة مع الزمن على نحو دوري، بتواتر زاوي: 4409-11
في حالة إضافة قوة محركة كهربائية خارجية متناوبة إلى الدارة السابقة فإن تواتر الاهتزازات الكهربائية في الدارة يكون منسجماً مع تواتر القوة الكهربائية الخارجية. أي أن الاهتزازة في هذه الحالة تكون قسرية. وأشهر مثال على ذلك تأثير الأمواج الكهرطيسية في دارة هوائي الاستقبال التلفزيوني.
من المفيد الإشارة إلى أن سعة الاهتزاز في الجملة متغير مع تواتر القوة الخارجية المطبقة على الجملة (القسرية)، مما يعني أن هناك سعة عظمى للاهتزاز توافق تواتراً معيناً، نقول في هذه الحالة إن الجملة في حالة تجاوب resonance.
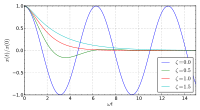
في الجمل المهتزة ونتيجة لوجود قوى احتكاك مختلفة ومقاومات تؤدي إلى استهلاك طاقة الاهتزاز وضياعها في أجزاء الجملة، فإن سعة الاهتزاز لن تكون ثابتة بل متناقصة مع الزمن على نحو تدريجي، أي أن الاهتزازة متخامدة damped oscillation (غير جيبيه) (الشكل-4).
الحركة الجيبية هي حالة خاصة من الحركة الاهتزازية. غير أنه يحصل في الكثير من الحالات تداخل (تراكب) الكثير من الحركات الجيبية بتواترات مختلفة ينتج منها حركة اهتزازية دورية غير جيبية. أو بالعكس يمكن وفقاً لنظرية فورييه تحليل الحركة الاهتزازية الدورية إلى مجموعة من الحركات الجيبية ذات تواترات تكون مضاعفات لإحداها.[3]
أمثلة
البندول البسيط
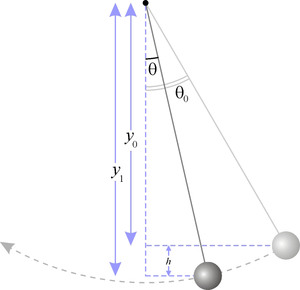
تأرجح البندول فوق القرص الدوار
Spring–mass system
تغير الطاقة في نظام التخميد الربيع
انظر أيضاً
- Anharmonic oscillator
- Critical speed
- Effective mass (spring-mass system)
- Normal mode
- Parametric oscillator
- Q factor
- Quantum harmonic oscillator
- Radial harmonic oscillator
الهوامش
- ^ Katsuhiko Ogata (2005). System Dynamics (4th ed.). University of Minnesota. p. 617.
- ^ Ajoy Ghatak (2005). Optics, 3E (3rd ed.). Tata McGraw-Hill. p. 6.10. ISBN 978-0-07-058583-6.
- ^ كنج الشوفي. "الحركة الاهتزازية". الموسوعة العربية.
المصادر
- Serway, Raymond A.; Jewett, John W. (2003). Physics for Scientists and Engineers. Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 1 (4th ed.). W. H. Freeman. ISBN 1-57259-492-6.
- Wylie, C. R. (1975). Advanced Engineering Mathematics (4th ed.). McGraw-Hill. ISBN 0-07-072180-7.