دالة دورية
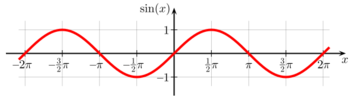
في الرياضيات، الدالة الدورية إنگليزية: Periodic Function هي دالة تكرر قيمتها بعد فترة زمنية محددة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التعريف
تكون الدالة ق (س) أقتران دوري أو دالة دورية ، دورتها أ إذا كانت قيمتها عند س تساوي قيمتها عند س + أ.
أي إن: ق (س) = ق (س + أ) حيث إن قيمة (أ) لا تساوي صفر.
وتسمى أصغر قيمة موجبة للعدد أ دورة الدالة ، والدوال المثلثية هي مثال عن الدوال الدورية أو الأقتران الدوري. فالجيب والجيب تمام والظل هي دوال دورية.
أمثلة
ومن الأمثلة على الدالة الدورية في الحياة اليومية كثيرة وعندما يتدخل الزمن في الأمر. فدوران الساعة، ومنازل القمر، وحركة القطارات والباصات كلها تتم وفق توابع دورية. حيث تعرف الحركة الدورية بأنها الحركة التي يشغل فيها الجسم المتحرك الموضع ذاته بعد مرور فترة زمنية معينة.
الخصائص
وظائف الدورة المزدوجة
Complex example
التعميمات
وظائف الدالة الدورية مضادة
Bloch-periodic functions
الحركة الدورية
هي حركة بعض الأجسام بحيث تعود إلى المسار نفسه الذي تسلكه في مدد زمنية متساوية، كما هي الحال في حركة القمر حول الأرض، أو الأرض حول الشمس، وعجلة سيارة متحركة بسرعة ثابتة، ونواس الساعة الجدارية وغير ذلك.
في هذا النوع من الحركات يعود الجسم المتحرك إلى النقطة التي بدأ منها الحركة خلال مدة زمنية محددة، يطلق على هذا الزمن اسم دور الحركة period ورمزه T، وهو الخاصة الأساسية المميزة للحركات الدورية والاهتزازية[ر]. في حين أن عدد الدورات أو الاهتزازات التي ينجزها المتحرك في ثانية واحدة يطلق عليه تواتر الحركة frequency ورمزه f ويقاس بالهرتز Hz، وهو يرتبط مع الدور بالعلاقة التالية f = 1/T.
يمكن أن تكون الحركة الدورية اهتزازية أيضاً، ويمكن التعبير عنها على هيئة تابع جيبي للزمن بردها إلى حركة جسيم على مسار دائري بسرعة ثابتة .
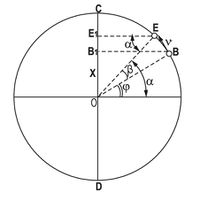
الجسيم B يتحرك بحركة منتظمة على المسار الدائري بسرعة زاوية ثابتة ω. مسقطه على أي من القطرين المتعامدين مثل CD سوف يكون متغيراً مع الزمن بشكل جيبي حول موضع التوازن O للنقطة المهتزة B1، حيث B1 مسقط B على CD. خلال دورة كاملة للجسيم B فان مسقطه B1 يتم اهتزازة كاملة، حيث ω = β/τ أو β = ωt، وβ طور الحركة. بفرض القطر الأفقي هو مبدأ حساب الزوايا، عندها تكون α = β+j أو α = ω t + j، حيث طور الحركة الابتدائي بحسب الشكل-1. إذن مسقط الجسيم وفق القطر CD في أي لحظة هو x = OE sin α أو بالشكل x = A sin α حيث x الإزاحة عن موضع التوازن في أي لحظة، A السعة العظمى OD. تبين هذه المعادلة الجيبية أن الجسيم يتحرك بحركة دورية. في حين أن ليس كل حركة دورية هي جيبية.
إن الحركات الدورية واسعة الانتشار في الطبيعة على وجه الخصوص. فلو نُظر إلى حركة الإلكترونات حول نواة الذرة أو إلى تعاقب الليل والنهار أو الفصول الأربعة، لوجدت جميعها تتكرر بصورة مستمرة وبأزمنة ثابتة.
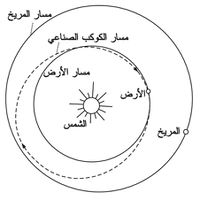
تتألف المجموعة الشمسية من الشمس وعدد من الكواكب حيث الكرة الأرضية واحدة منها. نتيجة للأبحاث التي قام بها كل من كيبرنيكوس Cepernicous ومن بعده كبلر Kepler ثم نيوتن Newton، بينت أن الشمس هي مركز هذه المجموعة بينما الكواكب الباقية تدور حولها في مدارات خاصة لها شكل قطع ناقص قريب من الدائري تقع الشمس في إحدى محرقيه. إن زمن الدورة الكاملة لكل كوكب حول الشمس يبقى ثابتاً، وهذا يعني أن حركة الكواكب حول الشمس هي حركة دورية. فعلى سبيل المثال دور حركة الأرض حول الشمس هو 365يوما أو 31.5مليون ثانية. كما يرافق حركة الأرض أيضاً حركة دورية للقمر حولها بدور قدره 28يوماً.[1]
انظر أيضاً
- تردد
- طول الموجة
- Periodic sequence
- Almost periodic function
- Amplitude
- Definite pitch
- Doubly periodic function
- Floquet theory
- Frequency
- Oscillation
- Quasiperiodic function
- Wavelength
- Periodic summation
المصادر
- ^ كنج الشوفي. "الحركات الدورية". الموسوعة العربية.
- Ekeland, Ivar (1990). "One". Convexity methods in Hamiltonian mechanics. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]. Vol. 19. Berlin: Springer-Verlag. pp. x+247. ISBN 3-540-50613-6. MR 1051888.
{{cite book}}: Invalid|ref=harv(help)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .